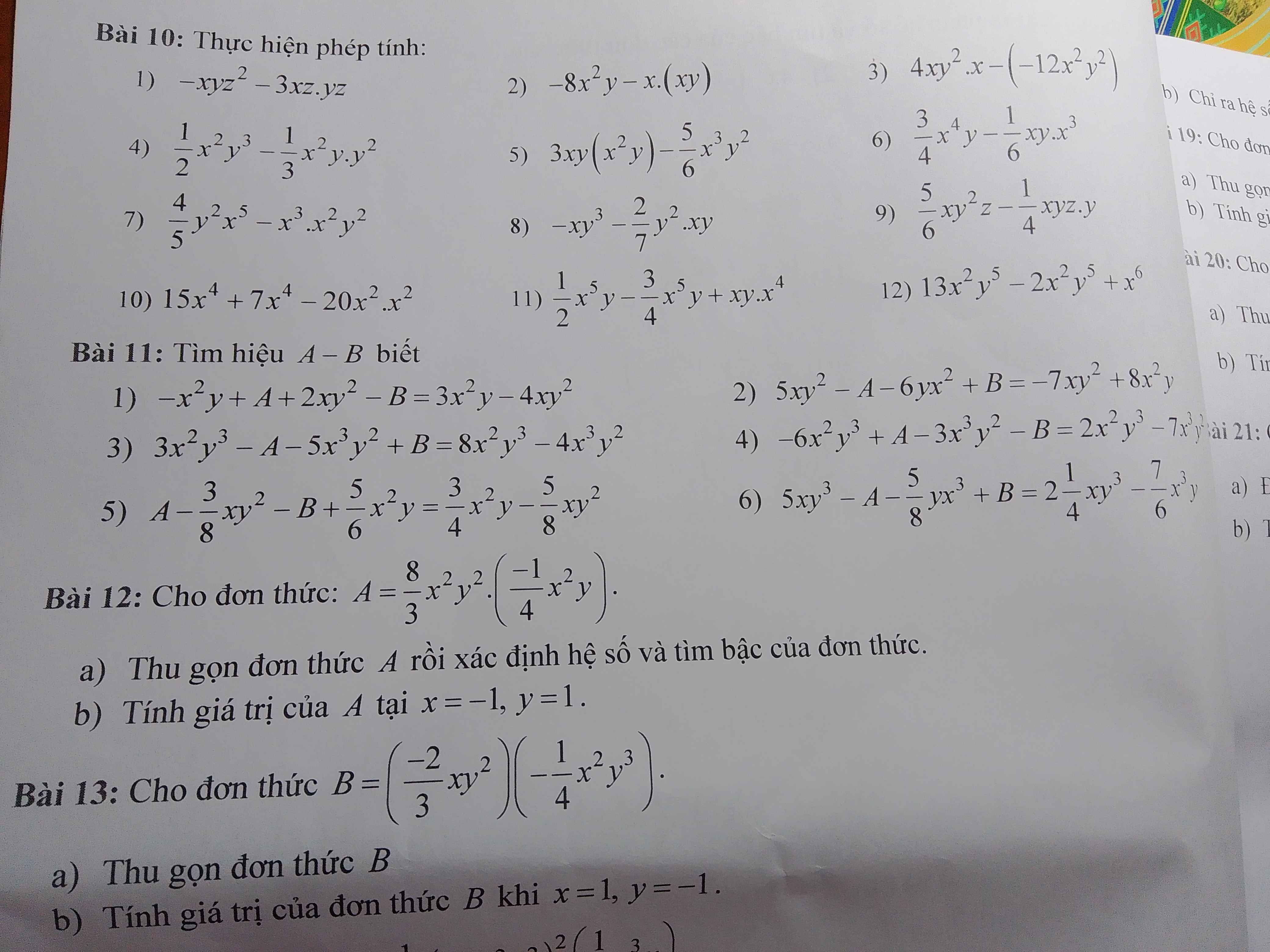\(\widehat{aOt}=\dfrac{\widehat{aOc}}{2}\)(Ot là phân giác của góc aOc)

\(\widehat{bOz}=\dfrac{\widehat{dOb}}{2}\)(Oz là phân giác của góc dOb)

mà \(\widehat{aOc}=\widehat{bOd}\)(hai góc đối đỉnh)

nên \(\widehat{aOt}=\widehat{bOz}\)

mà \(\widehat{aOt}+\widehat{bOt}=180^0\)(hai góc kề bù)

nên \(\widehat{bOt}+\widehat{bOz}=180^0\)

=>Ot và Oz là hai tia đối nhau

Gọi đường thẳng (d): y=ax+b(a\(\ne\)0) là đường thẳng đi qua hai điểm (2;0); (-1;-2)

Thay x=2 và y=0 vào (d), ta được:

\(a\cdot2+b=0\)(1)

Thay x=-1 và y=-2 vào (d), ta được:

\(a\cdot\left(-1\right)+b=-2\left(2\right)\)

Từ (1),(2) ta có hệ phương trình: \(\left\{{}\begin{matrix}2a+b=0\\-a+b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+b+a-b=0-\left(-2\right)\\b=-2a\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3a=2\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b=-2\cdot\dfrac{2}{3}=-\dfrac{4}{3}\end{matrix}\right.\)

Vậy: (d): \(y=\dfrac{2}{3}x-\dfrac{4}{3}\)

=>\(\dfrac{2}{3}x-y=\dfrac{4}{3}\)

Lời giải:

Gọi khối lượng đầu cá và thân cá lần lượt là $a$ và $b$ (gam). Theo bài ra ta có:

$a = \frac{1}{2}b+350$

$b=a+350$

Thay $b=a+350$ vào điều kiện ban đầu thì:

$a=\frac{1}{2}(a+350)+350$

$a=\frac{1}{2}a+525$

$\frac{1}{2}a=525$

$a=525.2=1050$

$b=a+350=1050+350=1400$ 

Khối lượng con cá: $a+b+350=1050+1400+350=2800$ (gam) hay $2,8$ kg.

Gọi thời gian ban đầu xe định đi từ A đến B là x(giờ)

(Điều kiện: x>1)

Độ dài quãng đường AB nếu đi với vận tốc 35km/h là:

35(x+2)(km)

Độ dài quãng đường AB nếu đi với vận tốc 50km/h là:

50(x-1)(km)

Do đó, ta có: 35(x+2)=50(x-1)

=>35x+70=50x-50

=>-15x=-120

=>x=8(nhận)

Thời điểm xe xuất phát là:

12h-8h=4h

Độ dài quãng đường AB là:

\(35\left(8+2\right)=35\cdot10=350\left(km\right)\)

Lời giải:

Thời gian ô tô chạy với vận tốc 35 km/h: $\frac{AB}{35}$ (h)

Thời gian ô tô chạy với vận tốc 50 km/h: $\frac{AB}{50}$ (h) 

Theo bài ra thì thời gian xe đi với vận tốc 35 km/h nhiều hơn thời gian xe đi với vận tốc 50 km/h $2+1=3$ (giờ)

Tức là:

$\frac{AB}{35}-\frac{AB}{50}=3$

$\Leftrightarrow \frac{3AB}{350}=3$

$\Leftrightarrow AB=350$ (km) 

Thời gian ô tô đi dự định đi hết quãng đường AB: $\frac{350}{35}-2=8$ (giờ)

Thời gian ô tô xuất phát: 12 giờ - 8 giờ = 4 giờ.

\(0,125+3.12+12,4\)

\(=0,125+36+12,4\)

\(=36,125+12,4\)

\(=48,525\)

48,525

Đề yêu cầu gì thế bạn?

bạn ơi cho mik hỏi là đề là phân tích thành nhân tử à?

a: ΔOAC cân tại O

mà OH là đường cao

nên OH là phân giác của góc AOC

Xét ΔOAD và ΔOCD có

OA=OC

\(\widehat{AOD}=\widehat{COD}\)

OD chung

Do đó: ΔOAD=ΔOCD

=>\(\widehat{OAD}=\widehat{OCD}\)

=>\(\widehat{OCD}=90^0\)

ΔOEB cân tại O

mà OF là đường trung tuyến

nên OF\(\perp\)BE

Ta có: \(\widehat{OAD}=\widehat{OCD}=\widehat{OFD}=90^0\)

=>O,A,C,F,D cùng thuộc đường tròn đường kính OD

1) $-xyz^2-3xz.yz=-xyz^2-3xyz^2=-4xyz^2$

2) $-8x^2y-x.(xy)=-8x^2y-x^2y=-9x^2y$

3) $4xy^2.x-(-12x^2y^2)=4x^2y^2+12x^2y^2=16x^2y^2$

4) $\frac12 x^2y^3-\frac13 x^2y.y^2=\frac12 x^2y^3-\frac13 x^2y^3=\frac16 x^2y^3$

5) $3xy.(x^2y)-\frac56 x^3y^2=3x^3y^2-\frac56 x^3y^2=\frac{13}{6}x^3y^2$

6) $\frac34 x^4y-\frac16 xy.x^3=\frac34 x^4y-\frac16 x^4y=\frac{7}{12}x^4y$

7) $\frac45y^2x^5-x^3.x^2y^2=\frac45 x^5y^2-x^5y^2=-\frac15 x^5y^2$

8) $-xy^3-\frac27 y^2.xy=-xy^3-\frac27 xy^3==\frac97 xy^3$

9) $\frac56 xy^2z-\frac14 xyz.y=\frac56 xy^2z-\frac14 xy^2z=\frac{7}{12} xy^2z$

10) $15x^4+7x^4-20x^2.x^2$

$=22x^4-20x^4=2x^4$

11) $\frac12 x^5y-\frac34 x^5y+xy.x^4$

$=-\frac14 x^5y+x^5y=\frac34 x^5y$

12) $13x^2y^5-2x^2y^5+x^6$

$=11x^2y^5+x^6$

Bài 10:

1: \(-xyz^2-3xz\cdot yz=-xyz^2-3xyz^2=-4xyz^2\)

2: \(-8x^2y-x\cdot xy=-8x^2y-x^2y=-9x^2y\)

3: \(4xy^2\cdot x-\left(-12x^2y^2\right)=4x^2y^2+12x^2y^2=16x^2y^2\)

4: \(\dfrac{1}{2}x^2y^3-\dfrac{1}{3}x^2y\cdot y^2=\dfrac{1}{2}x^2y^3-\dfrac{1}{3}x^2y^3=\dfrac{1}{6}x^2y^3\)

5: \(3xy\cdot\left(x^2y\right)-\dfrac{5}{6}x^3y^2=3x^3y^2-\dfrac{5}{6}x^3y^2=\dfrac{13}{6}x^3y^2\)

6: \(\dfrac{3}{4}x^4y-\dfrac{1}{6}xy\cdot x^3=\dfrac{3}{4}x^4y-\dfrac{1}{6}x^4y=x^4y\left(\dfrac{3}{4}-\dfrac{1}{6}\right)=\dfrac{7}{12}x^4y\)

7: \(\dfrac{4}{5}x^5y^2-x^3\cdot x^2y^2=\dfrac{4}{5}x^5y^2-x^5y^2=-\dfrac{1}{5}x^5y^2\)

8: \(-xy^3-\dfrac{2}{7}\cdot y^2\cdot xy=-xy^3-\dfrac{2}{7}xy^3=-\dfrac{9}{7}xy^3\)

9: \(\dfrac{5}{6}xy^2z-\dfrac{1}{4}xyz\cdot y=\dfrac{5}{6}xy^2z-\dfrac{1}{4}xy^2z=xyz^2\left(\dfrac{5}{6}-\dfrac{1}{4}\right)=\dfrac{7}{12}xyz^2\)

10:

\(15x^4+7x^4-20x^2\cdot x^2=22x^4-20x^4=2x^4\)

11:

\(\dfrac{1}{2}x^5y-\dfrac{3}{4}x^5y+xy\cdot x^4\)

\(=\dfrac{1}{2}x^5y-\dfrac{3}{4}x^5y+x^5y\)

\(=x^5y\left(\dfrac{1}{2}-\dfrac{3}{4}+1\right)=\dfrac{3}{4}x^5y\)

12: \(13x^2y^5-2x^2y^5+x^6=x^2y^5\left(13-2\right)+x^6=x^6+11x^2y^5\)

Với \(x>0;x\ne1\):

\(\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}+\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}-\dfrac{4}{\sqrt{x}}\right)\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)

\(=\left[\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}-\dfrac{4}{\sqrt{x}}\right]\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)

\(=\dfrac{x+\sqrt{x}+1+x-\sqrt{x}+1-4}{\sqrt{x}}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)

\(=\dfrac{2x-2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)

\(=\dfrac{2\left(x-1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{2\left(\sqrt{x}-1\right)^2}{\sqrt{x}}=\dfrac{2x-4\sqrt{x}+2}{\sqrt{x}}\)

Đề bài là rút gọn biểu thức