(\(\dfrac{12}{25}\))^{\(^x\)}  = (\(\dfrac{5}{3}\))^-2 - (-\(\dfrac{3}{5}\))⁴

(\(\dfrac{12}{25}\))^\(x\)  = (\(\dfrac{3}{5}\))² - (\(\dfrac{3}{5}\))⁴

(\(\dfrac{12}{25}\))^{\(^x\)} = \(\dfrac{9}{25}\) - \(\dfrac{81}{625}\)

(\(\dfrac{12}{25}\))^{\(^x\)}  = \(\dfrac{144}{625}\)

(\(\dfrac{12}{25}\))^{\(^x\)} = (\(\dfrac{12}{25}\))²

       \(x\) = 2

(12/25)ˣ = (5/3)⁻² - (-3/5)⁴

(12/25)ˣ = 9/25 - 81/625

(12/25)ˣ = 144/625

(12/25)ˣ = (12/25)²

x = 2

a) 1/20 - (x - 8/5) = 1/10

x - 8/5 = 1/20 - 1/10

x - 8/5 = -1/20

x = -1/20 + 8/5

x = 31/20

b) 7/4 - (x + 5/3) = -12/5

x + 5/3 = 7/4 + 12/5

x + 5/3 = 83/20

x = 83/20 - 5/3

x = 149/60

c) x - [17/2 - (-3/7 + 5/3)] = -1/3

x - (17/2 - 26/21) = -1/3

x - 305/42 = -1/3

x = -1/3 + 305/42

x = 97/14

a) \(\dfrac{2}{3}x-\dfrac{1}{2}x=\left(-\dfrac{7}{12}\right)\cdot1\dfrac{2}{5}\)

\(\Rightarrow\dfrac{1}{6}x=\left(-\dfrac{7}{12}\right)\cdot\dfrac{7}{5}\)

\(\Rightarrow\dfrac{1}{6}x=-\dfrac{49}{60}\)

\(\Rightarrow x=-\dfrac{49}{60}:\dfrac{1}{6}\)

\(\Rightarrow x=-\dfrac{49}{10}\) 

b) \(\left(\dfrac{1}{5}-\dfrac{3}{2}x\right)^2=\dfrac{9}{4}\)

\(\Rightarrow\left(\dfrac{1}{5}-\dfrac{3}{2}x\right)^2=\left(\pm\dfrac{3}{2}\right)^2\)

+) \(\dfrac{1}{5}-\dfrac{3}{2}x=\dfrac{3}{2}\)

\(\Rightarrow\dfrac{3}{2}x=\dfrac{1}{5}-\dfrac{3}{2}\)

\(\Rightarrow\dfrac{3}{2}x=-\dfrac{13}{10}\)

\(\Rightarrow x=-\dfrac{13}{10}:\dfrac{3}{2}\)

\(\Rightarrow x=-\dfrac{13}{15}\)

+) \(\left(1,25-\dfrac{4}{5}x\right)^3=-125\)

\(\Rightarrow\left(\dfrac{5}{4}-\dfrac{4}{5}x\right)^3=\left(-5\right)^3\)

\(\Rightarrow\dfrac{5}{4}-\dfrac{4}{5}x=-5\)

\(\Rightarrow\dfrac{4}{5}x=\dfrac{5}{4}+5\)

\(\Rightarrow\dfrac{4}{5}x=\dfrac{25}{4}\)

\(\Rightarrow x=\dfrac{25}{4}:\dfrac{4}{5}\)

\(\Rightarrow x=\dfrac{125}{16}\)

a, \(\dfrac{2}{3}\)\(x\) - \(\dfrac{1}{2}\)\(x\) = (- \(\dfrac{7}{12}\)). 1\(\dfrac{2}{5}\)

    \(x\).(\(\dfrac{2}{3}\) - \(\dfrac{1}{2}\)) = (- \(\dfrac{7}{12}\)) . \(\dfrac{7}{5}\)

    \(x\). \(\dfrac{1}{6}\) = - \(\dfrac{49}{60}\)

    \(x\)      = - \(\dfrac{49}{60}\).6

    \(x\)      = -\(\dfrac{49}{10}\)

16 + 4x = 2 ÷ 2

=> 16 + 4x = 1

=> 4x = 1 - 16

=> 4x = -15

=> x = -15/4

a) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)

\(2A=2\cdot\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{100}}\right)\)

\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{101}}\)

\(2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{99}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{100}}\)

\(A=1-\dfrac{1}{2^{100}}\)

b) \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2023\cdot2024}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\)

\(=1-\dfrac{1}{2024}\)

\(=\dfrac{2024}{2024}-\dfrac{1}{2024}\)

\(=\dfrac{2023}{2024}\)

cứu 

Câu 3

a) Số bánh mì đã bán buổi sáng:

200 . 3/5 = 120 (bánh)

Số tiền bán được buổi sáng:

120 . 15000 = 1800000 (đồng)

b) Giá bánh mì buổi chiều:

15000 - 15000.20% = 12000 (đồng)

Số bánh mì bán buổi chiều:

200 - 120 = 80 (bánh)

Số tiền bán bánh buổi chiều:

80 . 12000 = 960000 (đồng)

Số tiền cả ngày bán bánh:

1800000 + 960000 = 2760000 (đồng)

Câu 4

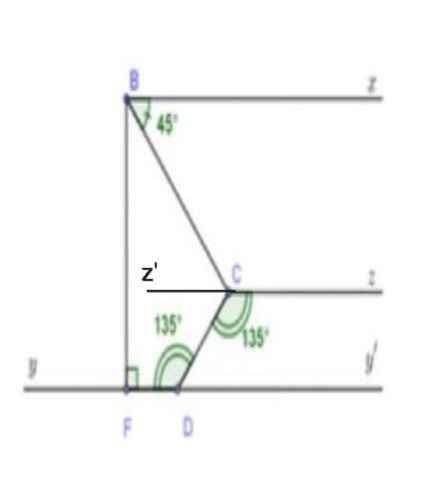  a) Ta có:

∠FDC = ∠DCz = 135⁰

Mà ∠FDC và ∠DCz là hai góc so le trong

⇒ Cz // Dy

b) Do Dy // Bx

Cz // Dy

⇒ Cz // Bx

Do Dy ⊥ BF

Dy // Bx

⇒ BF ⊥ Bx

⇒ ∠FBx = 90⁰

⇒ ∠FBC = ∠FBx - ∠CBx

= 90⁰ - 45⁰

= 45⁰

⇒ ∠FBC = ∠CBx = 45⁰

⇒ BC là tia phân giác của ∠FBx

c) Vẽ tia Cz' là tia đối của tia Cz

⇒ Cz' // Bx // Dy

Do Cz // Bx (cmt)

⇒ ∠BCz' = ∠CBx = 45⁰ (so le trong)

Ta có:

∠DCz' + ∠DCz = 180⁰ (kề bù)

⇒ ∠DCz' = 180⁰ - ∠DCz

= 180⁰ - 135⁰

= 45⁰

⇒ ∠DCz' = ∠BCz = 45⁰

⇒ Cz' là tia phân giác của ∠BCD

Do Ct là tia phân giác của ∠BCD

⇒ Ct ≡ Cz'

Mà Cz' // Dy (cmt)

⇒ Ct // Dy

Điểm trung bình môn Toán của An:

(7 + 8 + 9 + 10 + 8,5 . 2 + 9,5 . 3) : 9 ≈ 8,8

Độ cao của du khách so với mực nước biển:

-3,5 -3,5 . 2/3 - 1,5 = -22/3 (m)