Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\dfrac{3\left(x^2+1\right)}{3\left(x^2-x+1\right)}=\dfrac{2\left(x^2-x+1\right)+x^2+2x+1}{3\left(x^2-x+1\right)}=\dfrac{2}{3}+\dfrac{\left(x+1\right)^2}{3\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}}\ge\dfrac{2}{3}\)
\(P=\dfrac{2\left(x^2-x+1\right)-x^2+2x-1}{x^2-x+1}=2-\dfrac{\left(x-1\right)^2}{\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\le2\)
\(\Rightarrow\dfrac{2}{3}\le P\le2\)
Mà P nguyên \(\Rightarrow\left[{}\begin{matrix}P=1\\P=2\end{matrix}\right.\)
- Với \(P=1\Rightarrow\dfrac{x^2+1}{x^2-x+1}=1\Rightarrow x^2+1=x^2-x+1\)
\(\Rightarrow x=0\)
- Với \(P=2\Rightarrow\dfrac{x^2+1}{x^2-x+1}=2\Rightarrow x^2+x=2\left(x^2-x+1\right)\)
\(\Rightarrow x^2-2x+1=0\Rightarrow x=1\)
Vậy \(x=\left\{0;1\right\}\)

1: \(\dfrac{DM}{DE}=\dfrac{2}{5}\)
\(\dfrac{DN}{DF}=\dfrac{6}{15}=\dfrac{2}{5}\)
Do đó: \(\dfrac{DM}{DE}=\dfrac{DN}{DF}\)
2: Xét ΔDEF có \(\dfrac{DM}{DE}=\dfrac{DN}{DF}\)
nên MN//EF

Ta thấy: \(2024\equiv1\) (\(mod\) \(2023\))
\(20242024\equiv1909\) (\(mod\) \(2023\))
...
\(2024...2024:2023\) dư một số nào đó là một trong các số từ \(1\) đến \(2022\) (\(2023\) số).
* Xét \(2024\) số: \(2024;20242024;...;20242024...2024\) (Gồm \(2024\) bộ số \(2024\))
+ Lấy \(2024\) số trên chia cho \(2023\), ta có \(2024\) số dư từ \(0\) đến \(2022\).
\(\Rightarrow\) Tồn tại hai số chia cho \(2023\) có cùng số dư.
Giả sử hai số đó là \(a=2024...2024\) (\(i\) bộ số \(2024\)) và \(b=2024...2024\) (\(j\) bộ số \(2024\)) \(\left(1\le i\le j\le2024\right)\)
+ \(a-b=2024...2024\cdot10^{4i}\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\)
+ \(ƯCLN\left(10^{4i};2023\right)=1\)
\(\Rightarrow2024...2024\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\) \(\left(đpcm\right)\).

\(x^4-3x+2=x\left(x^3+ax^2+bx-2\right)-\left(x^3+ax^2+bx-2\right)\)
\(\Rightarrow x^4-3x+2=x^4+\left(a-1\right)x^3+\left(b-a\right)x^2-\left(b+2\right)x+2\)
Đồng nhất hệ số 2 vế ta được:
\(\left\{{}\begin{matrix}a-1=0\\b-a=0\\b+2=3\end{matrix}\right.\) \(\Rightarrow a=b=1\)
\(x^4-3x+2=\left(x-1\right)\left(x^3+ax^2+bx-2\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x^3+x^2+x-2\right)=\left(x-1\right)\left(x^3+ax^2+bx-2\right)\)
\(\Rightarrow x^3+x^2+x-2=x^3+ax^2+bx-2\)
\(\Rightarrow1\cdot x^2+1\cdot x=ax^2+bx\)
\(\Rightarrow a=1\) và \(b=1\)

\(B=3x^2+3y^2+z^2+5xy-3yz-3xz-2x-2y+3\\\Rightarrow4A=12x^2+12y^2+4z^2+20xy-12yz-12xz-8x-8y+12\\\\=[(9x^2+18xy+9y^2)-(12xz+12yz)+4z^2]+[(2x^2+4xy+2y^2)-(8x+8y)+8]+(x^2-2xy+y^2)+4\\=[(3x+3y)^2-2\cdot(3x+3y)\cdot2z+(2z)^2]+[2(x^2+2xy+y^2)-8(x+y)+8]+(x-y)^2+4\\=(3x+3y-2z)^2+2[(x+y)^2-4(x+y)+4]+(x-y)^2+4\\=(3x+3y-2z)^2+2(x+y-2)^2+(x-y)^2+4\)
Ta thấy: \(\left\{{}\begin{matrix}\left(3x+3y-2z\right)^2\ge0\forall x,y,z\\2\left(x+y-2\right)^2\ge0\forall x,y\\\left(x-y\right)^2\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left(3x+3y-2z\right)^2+2\left(x+y-2\right)^2+\left(x-y\right)^2+4\ge4\forall x,y,z\)
\(\Leftrightarrow4B\ge4\Leftrightarrow B\ge1\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}3x+3y-2z=0\\x+y-2=0\\x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=x\\2x=2\\2z=6x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\z=3\end{matrix}\right.\)
Vậy \(Min_B=1\) khi \(x=y=1;z=3\).
\(Toru\)

a: Xét ΔBAC có AM là phân giác
nên \(\dfrac{BM}{MC}=\dfrac{AB}{AC}\)
=>\(\dfrac{BM}{MC}=\dfrac{a}{b}\)
=>\(\dfrac{BM}{a}=\dfrac{MC}{b}\)
mà BM+MC=BC=a
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BM}{a}=\dfrac{MC}{b}=\dfrac{BM+MC}{a+b}=\dfrac{a}{a+b}\)
=>\(BM=\dfrac{a\cdot a}{a+b}=\dfrac{a^2}{a+b}\)
Xét ΔBCA có CN là phân giác
nên \(\dfrac{BN}{NA}=\dfrac{BC}{CA}\)
=>\(\dfrac{BN}{NA}=\dfrac{a}{b}\)
=>\(\dfrac{BN}{NA}=\dfrac{BM}{MC}\)
Xét ΔBAC có \(\dfrac{BN}{NA}=\dfrac{BM}{MC}\)
nên MN//AC
b: Xét ΔBAC có MN//AC
nên \(\dfrac{MN}{AC}=\dfrac{BM}{BC}\)
=>\(\dfrac{MN}{b}=\dfrac{a^2}{a+b}:a=\dfrac{a}{a+b}\)
=>\(MN=\dfrac{a\cdot b}{a+b}\)

a: 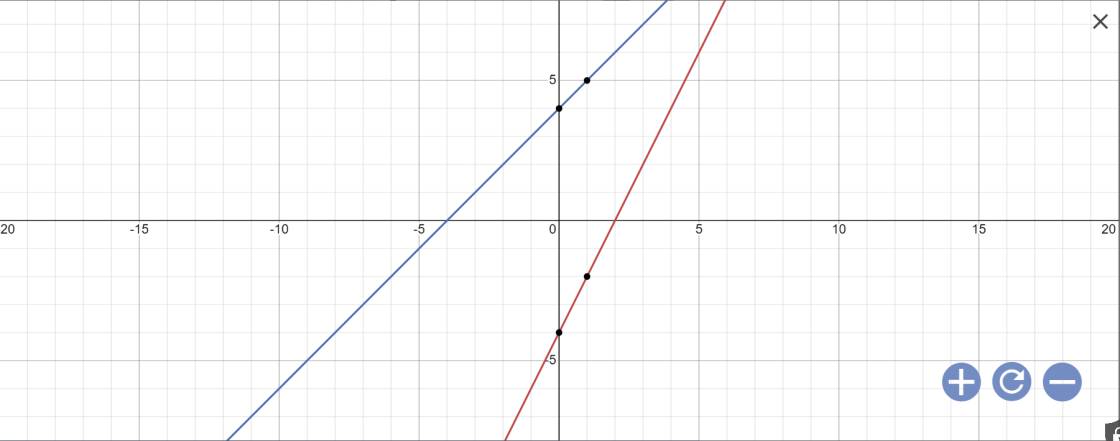
b: Phương trình hoành độ giao điểm là:
2x-4=x+4
=>2x-x=4+4
=>x=8
Thay x=8 vào y=x+4, ta được:
y=8+4=12
Vậy: Q(8;12)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: N(0;-4)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=0+4=4\end{matrix}\right.\)
Vậy: M(0;4)
M(0;4); N(0;-4); Q(8;12)
\(MN=\sqrt{\left(0-0\right)^2+\left(-4-4\right)^2}=8\)
\(MQ=\sqrt{\left(8-0\right)^2+\left(12-4\right)^2}=\sqrt{8^2+8^2}=8\sqrt{2}\)
\(NQ=\sqrt{\left(8-0\right)^2+\left(12+4\right)^2}=\sqrt{8^2+16^2}=8\sqrt{5}\)
Xét ΔMNQ có \(cosMNQ=\dfrac{NM^2+NQ^2-MQ^2}{2\cdot NM\cdot NQ}=\dfrac{256}{2\cdot8\cdot8\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
=>\(sinMNQ=\sqrt{1-\left(\dfrac{2}{\sqrt{5}}\right)^2}=\dfrac{1}{\sqrt{5}}\)
Diện tích ΔMNQ là:
\(S_{MNQ}=\dfrac{1}{2}\cdot NM\cdot NQ\cdot sinMNQ\)
\(=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{5}}\cdot8\cdot8\sqrt{5}=\dfrac{64}{2}=32\)

a: Để \(f\left(x\right)=\dfrac{2}{\left|x\right|-2}\) có nghĩa thì \(\left|x\right|-2\ne0\)
=>\(\left|x\right|\ne2\)
=>\(x\in R\backslash\left\{2;-2\right\}\)
b: Để \(f\left(x\right)=\dfrac{1}{2-x}+\dfrac{1}{x+3}\) có nghĩa thì \(\left\{{}\begin{matrix}2-x\ne0\\x+3\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\ne2\\x\ne-3\end{matrix}\right.\)

\(E=2\left(x^2+4xy+4y^2\right)+3y^2-4x-2y+6\)
\(=2\left(x+2y\right)^2-4\left(x+2y\right)+2+3y^2+6y+3+1\)
\(=2\left(x+2y-1\right)^2+3\left(y+1\right)^2+1\ge1\)
\(E_{min}=1\) khi \(\left\{{}\begin{matrix}x+2y-1=0\\y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
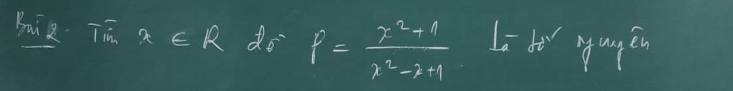
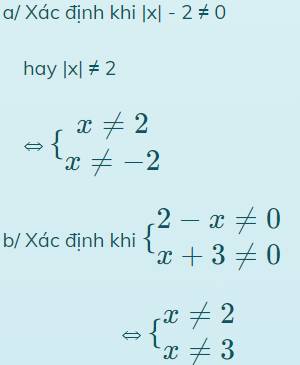
\(B=\dfrac{-\left(2x^2+3\right)+2x^2+x+5}{2x^2+3}=-1+\dfrac{2\left(x+\dfrac{1}{4}\right)^2+\dfrac{39}{8}}{2x^2+3}>-1\)
\(B=\dfrac{2x^2+3-2x^2+x-1}{2x^2+3}=1-\dfrac{2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}}{2x^2+3}< 1\)
\(\Rightarrow-1< B< 1\)
Mà B nguyên \(\Rightarrow B=0\)
\(\Rightarrow x+2=0\Rightarrow x=-2\)