2 ô tô đi từ A -> B cách nhau 200km biết vận tốc ô tô 1 nhanh hơn ô tô 2 là 10km/h nên ô tô 1 đến trước ô tô 2 là 1h . tính vận tốc của mỗi xe
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


$-\frac32-2x+\frac34=-2$
$\Rightarrow -\frac32-2x=-2-\frac34$
$\Rightarrow -\frac32-2x=-\frac{11}{4}$
$\Rightarrow 2x=-\frac32-(-\frac{11}{4})$
$\Rightarrow 2x=\frac54$
$\Rightarrow x=\frac54:2$
$\Rightarrow x=\frac58$

a: \(\left(\dfrac{1}{2}x^5-3x^2\right):x^2-x\left(\dfrac{1}{2}x^2+5\right)+2x\left(x-2\right)\left(x+2\right)-\left(x^3-27\right):\left(x-3\right)\)
\(=\dfrac{1}{2}x^3-3-\dfrac{1}{2}x^3-5x+2x\left(x^2-4\right)-\dfrac{\left(x-3\right)\left(x^2+3x+9\right)}{x-3}\)
\(=-5x-3+2x^3-8x-x^2-3x-9\)
\(=2x^3-x^2-16x-12\)
b: \(\left(7x^3-2x^2\right):\left(-2x^2\right)+\left(\dfrac{5}{4}x^2-3x\right):x-\dfrac{1}{2}x\left(x-1\right)\left(2x+1\right)\)
\(=\dfrac{-7}{2}x+1+\dfrac{5}{4}x-3-\dfrac{1}{2}x\left(2x^2+x-2x-1\right)\)
\(=-\dfrac{9}{4}x-2-\dfrac{1}{2}x\left(2x^2-x-1\right)\)
\(=-\dfrac{9}{4}x-2-x^3+\dfrac{1}{2}x^2+\dfrac{1}{2}x\)
\(=-x^3+\dfrac{1}{2}x^2-\dfrac{7}{4}x-2\)



b1: \(\dfrac{1}{-3}=\dfrac{-1}{3}=\dfrac{-10}{30}\)
\(\dfrac{-1}{4}=\dfrac{-10}{40}\)
=>3 số hữu tỉ xen giữa là \(-\dfrac{10}{31};-\dfrac{10}{33};-\dfrac{10}{37}\)
b2: \(\dfrac{-3}{7}=\dfrac{-3\cdot5}{7\cdot5}=\dfrac{-15}{35}=\dfrac{-150}{350};\dfrac{-2}{5}=\dfrac{-2\cdot7}{5\cdot7}=\dfrac{-14}{35}=-\dfrac{140}{350}\)
=>3 số hữu tỉ xen giữa là \(-\dfrac{149}{350};-\dfrac{147}{350};-\dfrac{145}{350}\)

a) Ta có MH//AC \(\left(\perp AB\right)\) nên \(\Delta BMH\sim\Delta BAC\)
\(\Rightarrow\dfrac{BM}{BA}=\dfrac{MH}{AC}\) \(\Rightarrow BM.AC=BA.MH\)
Tam giác ABH vuông tại H có đường cao HM
\(BA.MH=HB.HA\)
Tương tự, ta có: \(CN.AB=HC.HA\)
Cộng theo vế 2 hệ thức trên, ta được:
\(BA.MH+CN.AB=HB.HA+HC.HA=HA\left(HB+HC\right)=AH.BC\)
Ta có đpcm.
b) Tam giác ABH vuông tại H có đường cao HM nên \(AM.BM=MH^2\).
Tương tự, ta có \(AN.CN=HN^2\)
Do đó \(VT=AM.BM+AN.CN=MH^2+HN^2\)
Dễ thấy tứ giác AMHN là hình chữ nhật nên \(MH^2+HN^2=MN^2=AH^2\)
Tam giác ABC vuông tại A có đường cao AH nên \(AH^2=BH.CH\)
Từ đó suy ra \(VT=BH.CH=VP\)
Vậy đẳng thức được chứng minh.
c) Xét hệ trục tọa độ Axy với A là gốc tọa độ, \(Ax\equiv AC,Ay\equiv AB\)
Khi đó đặt \(B\left(0;b\right)\), \(C\left(c;0\right)\)
Khi đó phương trình đường thẳng \(BC:y=-\dfrac{b}{c}x+b\)
\(\Rightarrow\) Phương trình đường thẳng \(AH:y=\dfrac{c}{b}x\)
Khi đó hoành độ của điểm H chính là nghiệm của pt hoành độ giao điểm của AH và BC: \(\dfrac{c}{b}x_0=-\dfrac{b}{c}x_0+b\)
\(\Leftrightarrow\left(\dfrac{c}{b}+\dfrac{b}{c}\right)x_0=b\)
\(\Leftrightarrow\left(\dfrac{c^2+b^2}{bc}\right)x_0=b\)
\(\Leftrightarrow x_0=\dfrac{cb^2}{b^2+c^2}\)
\(\Rightarrow y_0=\dfrac{c}{b}x_0=\dfrac{c}{b}.\dfrac{cb^2}{b^2+c^2}=\dfrac{bc^2}{b^2+c^2}\)
Vậy \(H\left(\dfrac{cb^2}{b^2+c^2},\dfrac{bc^2}{b^2+c^2}\right)\)
Vì M là hình chiếu của H lên trục Oy \(\Rightarrow M\left(0,\dfrac{bc^2}{b^2+c^2}\right)\)
Tương tự \(\Rightarrow N\left(\dfrac{cb^2}{b^2+c^2},0\right)\)
Khi đó \(BM=BA-MA=b-\dfrac{bc^2}{b^2+c^2}=\dfrac{b^3+bc^2-bc^2}{b^2+c^2}=\dfrac{b^3}{b^2+c^2}\)
\(CN=CA-NA=c-\dfrac{cb^2}{b^2+c^2}=\dfrac{cb^2+c^3-cb^2}{b^2+c^2}=\dfrac{c^3}{b^2+c^2}\)
\(\Rightarrow\dfrac{BM}{CN}=\dfrac{\dfrac{b^3}{b^2+c^2}}{\dfrac{c^3}{b^2+c^2}}=\dfrac{b^3}{c^3}=\left(\dfrac{b}{c}\right)^3=\left(\dfrac{AB}{AC}\right)^3\)
\(\Rightarrow\sqrt[3]{\dfrac{MB}{NC}}=\dfrac{AB}{AC}\) (đpcm)

Ta có: \(x+y=\dfrac{a}{m}+\dfrac{b}{m}=\dfrac{a+b}{m}\)
\(\Rightarrow\dfrac{1}{2}\left(x+y\right)=\dfrac{1}{2}\cdot\dfrac{a+b}{m}=\dfrac{a+b}{2m}\)
\(\Rightarrow\dfrac{1}{2}\left(x+y\right)=z\)
\(\Rightarrow\dfrac{x+y}{2}=z\)
=> `z` là trung bình cộng của `x` và `y`
=> `z` nằm giữa `x` và `y`
Mà: `x<y`
=> `x<z<y`
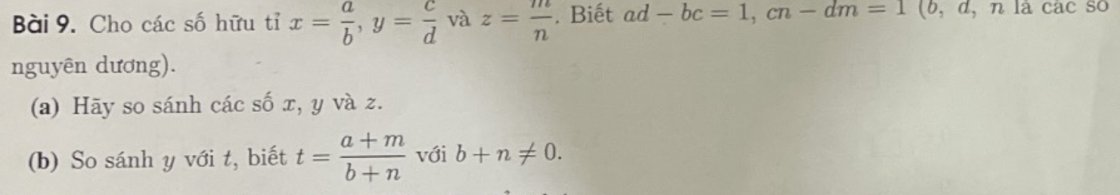 mn lm giup e vs
mn lm giup e vs

Gọi x (km/h) là vận tốc của ô tô 1 (x > 10)
Vận tốc của ô tô 2 là: x - 10 (km/h)
Thời gian ô tô 1 đi từ A đến B:
200x - 200x + 2000 = x² - 10x
x² - 10x - 2000 = 0
x² - 50x + 40x - 2000 = 0
(x² - 50x) + (40x - 2000) = 0
x(x - 50) + 40(x - 50) = 0
(x - 50)(x + 40) = 0
x - 50 = 0 hoặc x + 40 = 0
*) x - 50 = 0
x = 50 (nhận)
*) x + 40 = 0
x = -40 (loại)
Vậy vận tốc của xe ô tô 1 là 50 km/h, vận tốc của xe ô tô 2 là 50 - 10 = 40 km/h