1+2+3+......+x=36
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(\left(1+\dfrac{1}{10}\right)\cdot\left(1+\dfrac{1}{11}\right)\cdot\left(1+\dfrac{1}{12}\right)\cdot...\cdot\left(1+\dfrac{1}{119}\right)\cdot\left(1+\dfrac{1}{120}\right)\)
\(=\dfrac{11}{10}\cdot\dfrac{12}{11}\cdot\dfrac{13}{12}\cdot...\cdot\dfrac{120}{119}\cdot\dfrac{121}{120}\)
\(=\dfrac{11\cdot12\cdot13\cdot...\cdot120\cdot121}{10\cdot11\cdot12\cdot...\cdot119\cdot120}\)
\(=\dfrac{121}{10}\)
b) \(\left(1+\dfrac{2}{5}\right)\cdot\left(1+\dfrac{2}{7}\right)\cdot\left(1+\dfrac{2}{9}\right)\cdot...\cdot\left(1+\dfrac{2}{97}\right)\cdot\left(1+\dfrac{2}{99}\right)\)
\(=\dfrac{7}{5}\cdot\dfrac{9}{7}\cdot\dfrac{11}{9}\cdot...\cdot\dfrac{99}{97}\cdot\dfrac{101}{99}\)
\(=\dfrac{7\cdot9\cdot11\cdot...\cdot99\cdot101}{5\cdot7\cdot9\cdot...\cdot97\cdot99}\)
\(=\dfrac{101}{5}\)

b) \(B=\dfrac{7}{2\cdot5}+\dfrac{7}{5\cdot8}+...+\dfrac{7}{26\cdot29}\)
\(B=7\cdot\left(\dfrac{1}{2\cdot5}+\dfrac{1}{5\cdot8}+...+\dfrac{7}{26\cdot29}\right)\)
\(B=\dfrac{7}{3}\cdot\left(\dfrac{3}{2\cdot5}+\dfrac{3}{5\cdot8}+...+\dfrac{3}{26\cdot29}\right)\)
\(B=\dfrac{7}{3}\cdot\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{26}-\dfrac{1}{29}\right)\)
\(B=\dfrac{7}{3}\cdot\left(\dfrac{1}{2}-\dfrac{1}{29}\right)\)
\(B=\dfrac{7}{3}\cdot\dfrac{27}{58}\)
\(B=\dfrac{63}{58}\)

a)
Tổng số bài kiểm tra lớp 6A là:
\(8:\dfrac{1}{5}=40\left(bài\right)\)
b) Số bài loại yếu lớp 6A chiếm số phần trong tổng số bài kiểm tra là:
\(1-\left(\dfrac{3}{10}+\dfrac{1}{4}\right)=\dfrac{9}{20}\)
Số bài loại yếu lớp 6A là:
\(40\cdot\dfrac{9}{20}=18\left(bài\right)\)
Đáp số:a) 40 bài b) 18 bài

\(\dfrac{x}{9}\cdot\dfrac{-7}{8}+\dfrac{x}{9}:\dfrac{-8}{17}=\dfrac{5}{7}\)
\(\dfrac{x}{9}\cdot\dfrac{-7}{8}+\dfrac{x}{9}\cdot\dfrac{17}{-8}=\dfrac{5}{7}\)
\(\dfrac{x}{9}\left(\dfrac{-7}{8}+\dfrac{17}{-8}\right)=\dfrac{5}{7}\)
\(\dfrac{x}{9}\cdot\left(-3\right)=\dfrac{5}{7}\)
\(\dfrac{x}{9}=-\dfrac{5}{21}\)
\(x=\dfrac{5\cdot9}{-21}\)
\(x=\dfrac{-15}{7}\)

a)
Điều kiện xác định: \(2n\ne4\Rightarrow n\ne2\)
Để A là phân số thì \(2n\in Z\Rightarrow n\in Z\)
Vậy mọi \(n\in Z,n\ne2\) thì A là phân số.
b)
\(A=\dfrac{2n+2}{2n-4}\)
\(A=\dfrac{2n-4+6}{2n-4}\)
\(A=1+\dfrac{6}{2n-4}\)
\(\Rightarrow2n-4\inƯ\left(6\right)\)
\(Ư\left(6\right)=\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
Ta loại các ước số lẻ.
| 2n-4 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| n | loại | loại | 3 | 1 | loại | loại | 5 | 1 |
Vậy \(n\in\left\{1;-1;3;5\right\}\)

\(\dfrac{5}{6}+\dfrac{11}{12}+\dfrac{19}{20}+\dfrac{29}{30}+\dfrac{41}{42}+\dfrac{55}{56}+\dfrac{71}{72}+\dfrac{89}{90}\)
\(=\left(1-\dfrac{1}{6}\right)+\left(1-\dfrac{1}{12}\right)+\left(1-\dfrac{1}{20}\right)+\left(1-\dfrac{1}{30}\right)+\left(1-\dfrac{1}{42}\right)+\left(1-\dfrac{1}{56}\right)+\left(1-\dfrac{1}{72}\right)+\left(1-\dfrac{1}{90}\right)\)
\(=8-\left(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\right)\)
\(=8-\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}\right)\)
\(=8-\left(\dfrac{3-2}{2\cdot3}+\dfrac{4-3}{3\cdot4}+\dfrac{5-4}{4\cdot5}+\dfrac{6-5}{5\cdot6}+\dfrac{7-6}{6\cdot7}+\dfrac{8-7}{7\cdot8}+\dfrac{9-8}{8\cdot9}+\dfrac{10-9}{9\cdot10}\right)\)
\(=8-\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\right)\)
\(=8-\left(\dfrac{1}{2}-\dfrac{1}{10}\right)\)
\(=8-\dfrac{4}{10}\)
\(=\dfrac{80}{10}-\dfrac{4}{10}=\dfrac{76}{10}=\dfrac{38}{5}\)

\(A=\dfrac{3}{2^2}+\dfrac{8}{3^2}+...+\dfrac{2023^2-1}{2023^2}\)
\(A=\dfrac{2^2-1}{2^2}+\dfrac{3^2-1}{3^2}+...+\dfrac{2023^2-1}{2023^2}\)
\(A=\left(\dfrac{2^2}{2^2}-\dfrac{1}{2^2}\right)+\left(\dfrac{3^2}{3^2}-\dfrac{1}{3^2}\right)+...+\left(\dfrac{2023^2}{2023^2}-\dfrac{1}{2023^2}\right)\)
\(A=1-\dfrac{1}{2^2}+1-\dfrac{1}{3^2}+...+1-\dfrac{1}{2023^2}\)
\(A=2022-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2023^2}\right)\)
Mà:
\(\dfrac{1}{2\cdot2}+\dfrac{1}{3\cdot3}+...+\dfrac{1}{2023\cdot2023}< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{2022\cdot2023}\)
Hay:
\(\dfrac{1}{2\cdot2}+\dfrac{1}{3\cdot3}+...+\dfrac{1}{2023\cdot2323}< 1-\dfrac{1}{2023}< 1\)
Nên:
\(\dfrac{1}{2\cdot2}+\dfrac{1}{3\cdot3}+...+\dfrac{1}{2023\cdot2323}< 1\)
Vậy A không phải là số tự nhiên.

\(\dfrac{12}{-15}=\dfrac{12:-3}{-15:-3}=\dfrac{-4}{5}\)
Ta có:
Mẫu số chung 2 phân số: 95
\(\dfrac{-4}{5}=\dfrac{-4\cdot19}{5\cdot19}=\dfrac{-76}{95}\)
\(\dfrac{-15}{19}=\dfrac{-15\cdot5}{19\cdot5}=\dfrac{-75}{95}\)
Vì \(-76< -75\) nên\(\dfrac{-76}{95}< \dfrac{-75}{95}\)
Vậy \(\dfrac{12}{-15}< \dfrac{-15}{19}\)
Rút gọn:
\(\dfrac{12}{-15}=\dfrac{12:3}{-15:3}=\dfrac{4}{-5}\)
Ta có:
\(\dfrac{4}{-5}\) và \(\dfrac{15}{-19}\) (Đổi \(\dfrac{-15}{19}=\dfrac{15}{-19}\))
Quy đồng 2 phân số:
Mẫu số chung: \(95\).
Ta có:
\(\dfrac{4}{-5}=\dfrac{4\cdot\left(-19\right)}{-5\cdot\left(-19\right)}=\dfrac{-76}{95};\dfrac{15}{-19}=\dfrac{15\cdot\left(-5\right)}{-19\cdot\left(-5\right)}=\dfrac{-75}{95}\)
Mà \(\dfrac{76}{95}>\dfrac{75}{95}\Rightarrow\dfrac{-76}{95}< \dfrac{-75}{95}\)
Vậy \(\dfrac{12}{-15}< \dfrac{-15}{19}\)
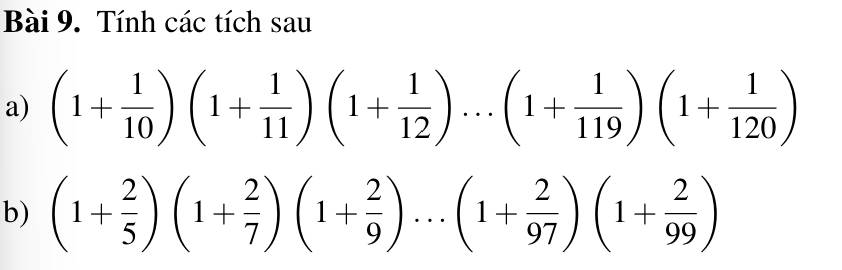
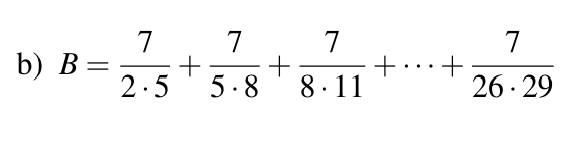
`1+2+3+...+x=36`
`⇒ [(x-1):1+1]×(x+1):2=36`
`⇒ (x-1+1)×(x+1):2=36`
`⇒x×(x+1)=36×2`
`⇒x^2+x=72`
`⇒x^2+x-72=0`
`⇒x^2-8x+9x-72=0`
`⇒x(x-8) + 9(x-8)=0`
`⇒(x-8)(x+9)=0`
TH1: `x-8=0`
`⇒x=8`
TH2: `x+9=0`
`⇒x=-9`
Vậy: ....
bn nói cụ thể hơn nha
X là số mấy bn ko ghi ra là số mấy thì bọn mình làm sao biết mà giải đc