cho hai tia Om và On là hai tia đối nhau biết moa=70° a)tính mOn b)vẽ Ot là tia phân giác tOn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(y=\dfrac{x+1}{x-2}\)
\(y'=-\dfrac{3}{\left(x-2\right)^2}< 0\forall x\inℝ\ \left\{2\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
b) \(y=\dfrac{2x+1}{x-1}\)
\(y'=-\dfrac{3}{\left(x-1\right)^2}< 0\forall x\inℝ\ \left\{1\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;1\right)\) và \((1;+\infty)\)

TA CÓ:a:5 dư 3 suy ra:a+2 chia hết cho 5
suy ra a+17 chia hết cho 5 (1)
a:7 dư 4 suy ra a+3 chia hết cho 7
suy ra a+17 chia hết cho 7 (2)
Từ (1) và (2) suy ra a+17 thuộc BC của 7 và 5
mà a nhỏ nhất nên a+17 thuộc BCNN của 7 và 5=35
suy ra a=35-17=18
Vậy a=18
TICK CHO MIK VỚI NHÉ

Số lít dầu trong 1 hũ là 36:12=3(lít)
Số lít mật ong còn lại là:
3x(12-3)=27(lít)

Đổi: 2 giờ 30 phút = 150 phút và 2 giờ 20 phút = 140 phút
Tỉ số thời gian máy bay thứ nhất so với máy bay thứ hai là: \(\dfrac{150}{140}=\dfrac{15}{14}\)
Cùng một quãng đường AB, thời gian và vận tốc là 2 đại lượng tỉ lệ nghịch
Do đó nên tỉ số vận tốc máy bay thứ nhất so với máy bay thứ hai là: \(\dfrac{14}{15}\)
Coi vận tốc máy bay thứ nhất có giá trị 14 phần, vận tốc máy bay thứ hai có giá trị 15 phần
Hiệu số phần bằng nhau: 15-14=1 (phần)
Vận tốc máy bay thứ nhất: 1:1x14=14 (km/p) = 840 (km/giờ)
Vận tốc máy bay thứ hai: 14+1=15(km/p)=900(km/giờ)
Một phút máy bay thứ nhất bay chậm hơn máy bay thứ hai 1km tức một giờ máy bay thứ nhất chậm hơn máy bay thứ hai 60 km . Nói cách khác là vận tốc của hai máy bay có hiệu là 60km/h
Thời gian máy bay thứ nhất bay là : 2 giờ 30 phút = 5/2giờ
Thời gian máy bay thứ hai bay là : 2 giờ 20 phút = 7/3giờ
Do cùng quãng đường bay nên tỉ số vận tốc hai máy bay tỉ lệ nghịch với tỉ số thời gian .
Ta có tỉ lệ :
Vận tốc máy bay thứ nhất/Vận tốc máy bay thứ hai = Thời gian máy bay hai bay/thời gian máy bay nhất bay
= 7/3:5/2= 14/15
Vẽ sơ đồ hiệu số phần bằng nhau là : 15 - 14 = 1 (phần)
Hiệu hai vận tốc là 60km/giờ.
Vậy máy bay thứ nhất bay :
60:1𝑥14=840( km/h )
Máy bay thứ hai bay là :
60:1𝑥15=900( km/h )

Cách 1:
Gọi số phải tìm là: \(\overline{ab}\) (\(a\inℕ^∗;b\inℕ;a,b\le9\))
Theo bài ra, ta có:
\(b\times8=\overline{ab}\\ b\times8=\overline{a0}+b\\ b\times8-b=a\times10\\ b\times7=a\times10\\ b\times7:10=a\\ b\times0,7=a\)
Thử lần lượt b từ 0 đến 9, nếu giá trị nào cho a là STN khác 0 và a bé hơn hoặc bằng 9 thì nhận
Kết quả: Không có giá trị nào thỏa mãn. Vậy không tìm được số thỏa mãn đề bài
Cách 2: Tương tự đến \(b\times7=\overline{a0}\)
Nhận thấy các số từ 0 đến 9 không có số nào nhân với 7 ra được số có tận cùng là 0
( Số 0 bị loại do 0 x 7 = 0 không phải số có 2 chữ số )

Bài 5:
x-y-3=0
=>x-y=3
\(M=x^3-x^2y-3x^2+xy-y^2-4y+x+2021\)
\(=x^2\left(x-y\right)-3x^2+y\left(x-y\right)-4y+x+2021\)
\(=3x^2-3x^2+3y-4y+x+2021\)
=x-y+2021
=3+2021
=2024
Bài 4:
x=2999 nên x+1=3000
\(F\left(x\right)=x^{99}-3000x^{98}+3000x^{97}-...+3000x-1\)
\(=x^{99}-x^{98}\left(x+1\right)+x^{97}\left(x+1\right)-...+x\left(x+1\right)-1\)
\(=x^{99}-x^{99}-x^{98}+x^{98}+x^{97}-...+x^2+x-1\)
=x-1
=2998
Bài 3:
a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
BA=BD
Do đó: ΔBAM=ΔBDM
=>MA=MD
Xét ΔMAN vuông tại A và ΔMDC vuông tại D có
MA=MD
\(\widehat{AMN}=\widehat{DMC}\)(hai góc đối đỉnh)
Do đó: ΔMAN=ΔMDC
=>MN=MC
=>ΔMNC cân tại M
b: Ta có: ΔMAN=ΔMDC
=>AN=DC
Ta có: BA+AN=BN
BD+DC=BC
mà BA=BD và AN=DC
nên BN=BC
=>B nằm trên đường trung trực của NC(1)
Ta có: MN=MC
=>M nằm trên đường trung trực của NC(2)
Ta có: IN=IC
=>I nằm trên đường trung trực của NC(3)
Từ (1),(2),(3) suy ra B,M,I thẳng hàng

Ta có:
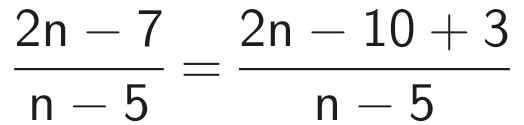
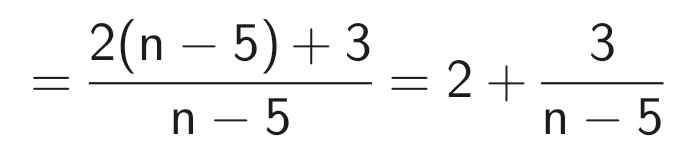
Để M nguyên thì 3 ⋮ (n - 5)
⇒ n - 5 ∈ Ư(3) = {-3; -1; 1; 3}
⇒ n ∈ {2; 4; 6; 8}
Vậy n {2; 4; 6; 8} thì M nguyên
TH1
=> |x-3| = x - 3 = 2x + 4
=> x - 2x = 4 + 3
=> -x = 7 <=> x = -7
x < 0
=> |x-3| = -x + 3 = 2x + 4
=> -x - 2x = 4-3
=> -3x = 1
=> x= -1/3

a: ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
Xét ΔDHA vuông tại H và ΔDAB vuông tại A có
\(\widehat{HDA}\) chung
Do đó: ΔDHA~ΔDAB
=>\(\dfrac{DH}{DA}=\dfrac{AH}{AB}=\dfrac{DA}{DB}\)
=>\(\dfrac{DH}{6}=\dfrac{AH}{8}=\dfrac{6}{10}=\dfrac{3}{5}\)
=>\(DH=6\cdot\dfrac{3}{5}=3,6\left(cm\right);AH=8\cdot\dfrac{3}{5}=4,8\left(cm\right)\)
b: \(\dfrac{DH}{DA}=\dfrac{DA}{DB}\)
=>\(DA^2=DH\cdot DB\)
mà DA=BC
nên \(BC^2=DH\cdot DB\)
c: Xét ΔBME vuông tại M và ΔFMD vuông tại M có
\(\widehat{MBE}=\widehat{MFD}\left(=90^0-\widehat{ADB}\right)\)
Do đó: ΔBME~ΔFMD
e: Xét ΔFDB có
FM,BA là các đường cao
FM cắt BA tại E
Do đó: E là trực tâm của ΔFDB
=>DE\(\perp\)FB
mà DE\(\perp\)KB
và FB,KB có điểm chung là B
nên F,K,B thẳng hàng
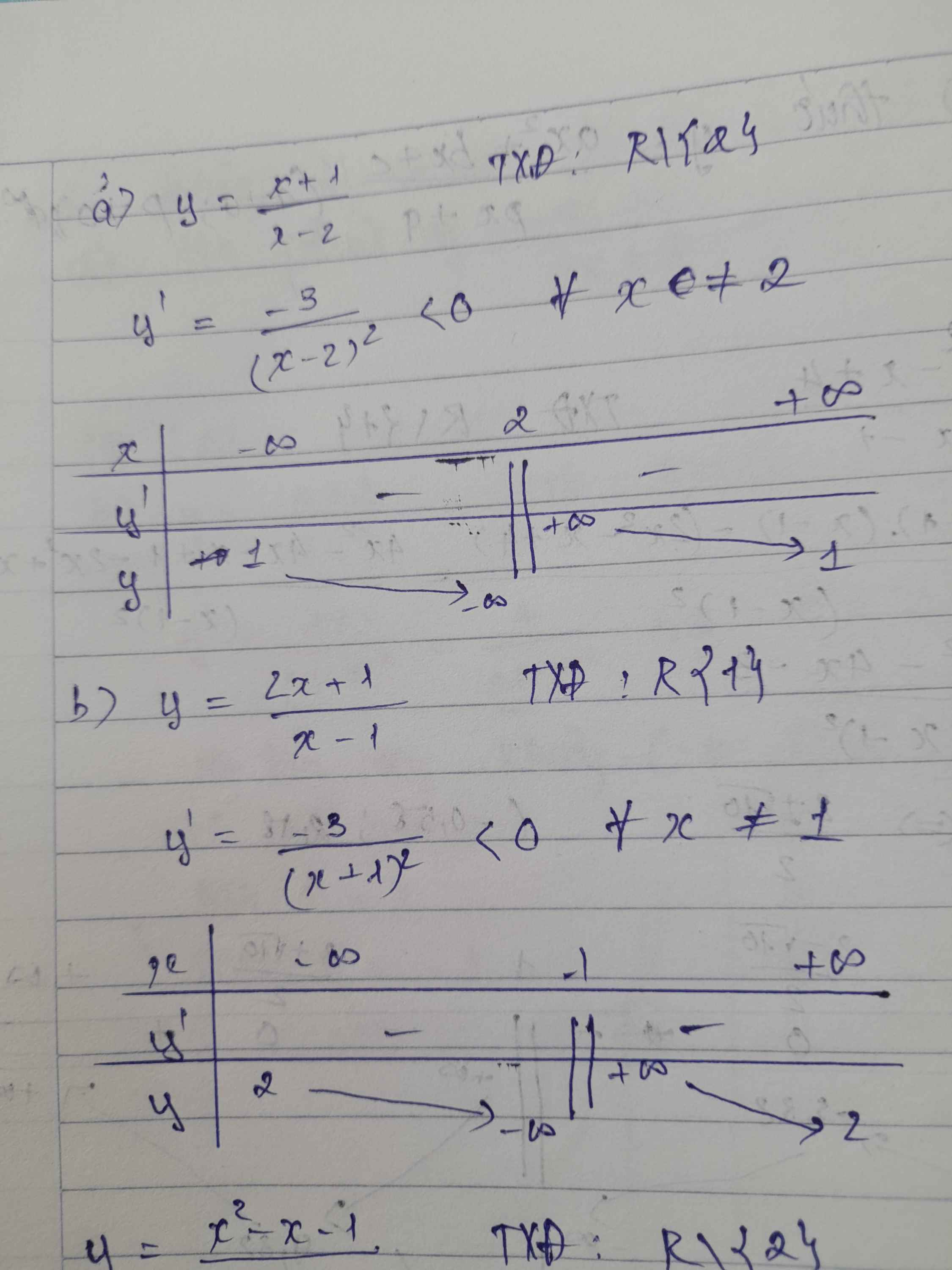


Thầy nghĩ là em ghi sai đề cả 2 câu a và b.
Em xem lại đề nhé!