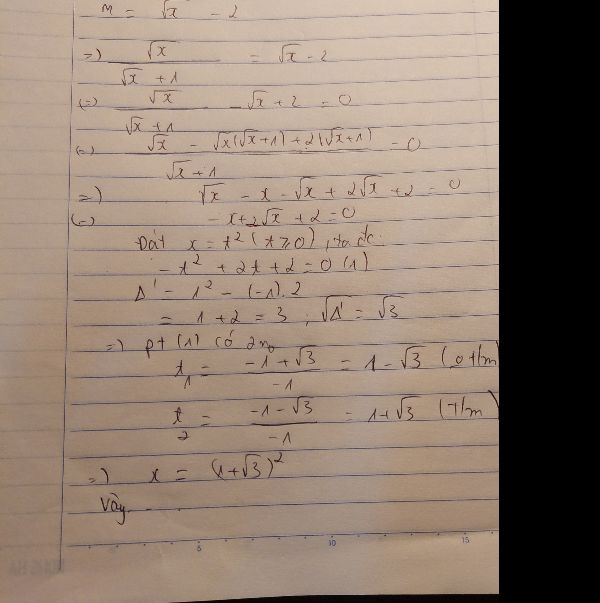Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=\frac{\sqrt{x}}{\sqrt{x}+1}\left(x\ge0\right)\)
Khi \(M=\sqrt{x}-2\)
\(\Rightarrow\frac{\sqrt{x}}{\sqrt{x}+1}=\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow\sqrt{x}=x+\sqrt{x}-2\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=x-\sqrt{x}-2\)
\(\Leftrightarrow x-\sqrt{x}-\sqrt{x}-2=0\)
\(\Leftrightarrow x-2\sqrt{x}+1-3=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=3\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=\left(\pm\sqrt{3}\right)^2\)
\(\Leftrightarrow\sqrt{x}-1=\pm\sqrt{3}\)
\(\Leftrightarrow\sqrt{x}=\pm\sqrt{3}+1\)
\(\Leftrightarrow\orbr{\begin{cases}x=\left(\sqrt{3}+1\right)^2\\x=\left(-\sqrt{3}+1\right)^2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3+2\sqrt{3}+1\\1-2\sqrt{3}+3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4+2\sqrt{3}\\x=4-2\sqrt{3}\end{cases}}\)
Vậy \(x\in\left\{4\pm2\sqrt{3}\right\}\)khi \(M=\sqrt{x}-2\)


\(\sqrt{3x^2-12x+21}+\sqrt{5x^2-20x+24}=-2x^2+8x-3\)
\(\left(\sqrt{3x^2-12x+21}-3\right)+\left(\sqrt{5x^2-20x+24}-2\right)=-2x^2+8x-8\)
\(\frac{3x^2-12x+21-9}{\sqrt{3x^2-12x+21}+3}+\frac{5x^2-20x+24-4}{\sqrt{5x^2-20x+24}+3}=\left(x-2\right)\left(4-2x\right)\)
\(\frac{3x^2-12x+12}{\sqrt{3x^2-12x+21}+3}+\frac{5x^2-20x+20}{\sqrt{5x^2-20x+24}+3}=\left(x-2\right)\left(4-2x\right)\)
\(\frac{\left(x-2\right)\left(3x-6\right)}{\sqrt{3x^2-12x+21}+3}+\frac{\left(x-2\right)\left(5x-10\right)}{\sqrt{5x^2-20x+24}+3}=\left(x-2\right)\left(4-2x\right)\)
\(\left(x-2\right)\left(\frac{3x-6}{\sqrt{3x^2-12x+21}+3}+\frac{5x-10}{\sqrt{5x^2-20x+24}}-4+2x\right)=0\)
\(\orbr{\begin{cases}x=2\left(TM\right)\\\frac{3x-6}{\sqrt{3x^2-12x+21}+3}+\frac{5x-10}{\sqrt{5x^2-20x+24}}-4+2x\ne0\left(KTM\right)\end{cases}}\)
vậy pt có nghiệm duy nhất là 2
Mà bạn ơi, tại sao cái về sau khác 0 được vậy bạn ? Sao mình không đặt (x-2)^2 luôn nhỉ? Dù sao cũng cảm ơn ha!