
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 31:
Ta có: \(4=2x+xy\ge2\sqrt{2x.xy}=2\sqrt{2}\sqrt{A}\)
suy ra \(A\le\frac{4^2}{2^2.2}=2\).
Dấu \(=\)khi \(\hept{\begin{cases}2x=xy\\2x+xy=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\).
Câu 10:
ĐK: \(x\inℝ\).
Ta có:
\(VT=\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+21}\)
\(=\sqrt{3x^2+6x+3+4}+\sqrt{5x^2+10x+5+16}\)
\(=\sqrt{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+16}\)
\(\ge\sqrt{4}+\sqrt{16}=2+4=6\).
Dấu \(=\)khi \(x+1=0\Leftrightarrow x=-1\).
\(VP=5-2x-x^2=6-\left(x^2+2x+1\right)=6-\left(x+1\right)^2\le6\)
Dấu \(=\)khi \(x+1=0\Leftrightarrow x=-1\).
Do đó nghiệm của phương trình đã cho là \(x=-1\).

a, ta có x=9
\(\Rightarrow\)\(A=\frac{\sqrt{9}+1}{\sqrt{9}-1}\)
\(=\frac{3+1}{3-1}=2\)
b,
\(B=\left(\frac{\sqrt{x}+1}{\sqrt{x}-1}-\frac{\sqrt{x}-1}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\left(\frac{\left(\sqrt{x}+1\right)^2}{x-1}-\frac{\left(\sqrt{x}-1\right)^2}{x-1}\right):\frac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\left(\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{x-1}\right):\frac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\frac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x+1}\right)}{x-\sqrt{x}}\)
\(=\frac{\sqrt{x}-x}{x-\sqrt{x}}\)
\(=-1\)
mik làm còn thiếu nhé (mik làm hơi tắt nếu ko hiểu có thể hỏi lại)

\(A=\frac{x-2\sqrt{x}+9}{\sqrt{x}-3}\)
Thay x = 3 vào A ta được : \(A=\frac{3-2\sqrt{3}+9}{\sqrt{3}-3}=\frac{12-2\sqrt{3}}{\sqrt{3}-3}=\frac{\left(12-2\sqrt{3}\right)\left(\sqrt{3}+3\right)}{3-9}\)
\(=\frac{12\sqrt{3}+36-6-6\sqrt{3}}{-6}=-2\sqrt{3}-5+\sqrt{3}=-5-\sqrt{3}\)




1, \(\sqrt{3x-6}=3\)đk : x >= 2
\(\Leftrightarrow3x-6=9\Leftrightarrow x=5\)
3, \(\sqrt{2x+1}=\sqrt{x}\)đk : \(\hept{\begin{cases}x\ge-\frac{1}{2}\\x\ge0\end{cases}}\Leftrightarrow x\ge0\)
\(\Leftrightarrow2x+1=x\Leftrightarrow x=-1\)( loại )
5, \(\sqrt{4\left(x+2\right)^2}=8\Leftrightarrow2\left|x+2\right|=8\Leftrightarrow\left|x+2\right|=4\)
TH1 : \(x+2=4\Leftrightarrow x=2\)
TH2 : \(x+2=-4\Leftrightarrow x=-6\)
7, \(\sqrt{x-1}=2-x\)đk : \(\hept{\begin{cases}x-1\ge0\\2-x\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge1\\x\le2\end{cases}}\Leftrightarrow1\le x\le2\)
\(\Leftrightarrow x-1=x^2-4x+4\Leftrightarrow x^2-5x+5=0\)
\(\Leftrightarrow x_1=\frac{5+\sqrt{5}}{2}\left(ktm\right);x_2=\frac{5-\sqrt{5}}{2}\left(tm\right)\)


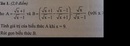

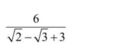
 câu 2 b) ,c) làm sao v m.n
câu 2 b) ,c) làm sao v m.n