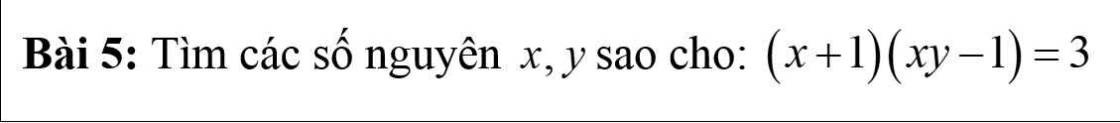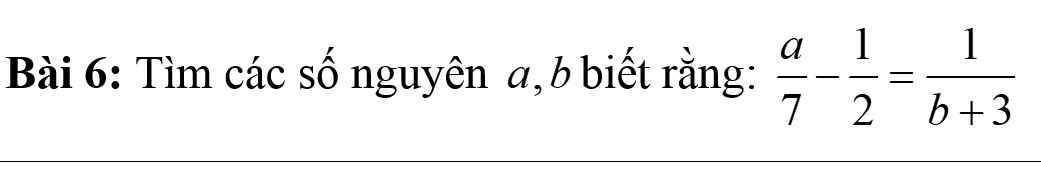150 ⋮ \(x\); \(x\in\) Z

\(x\) \(\in\) Ư(150)

150 = 2.3.5²

\(x\in\) Ư(150) = {1; 2; 3; 5; 6; 10; 15; 25; 30; 50; 75; 150}

Đề lỗi hiển thị rồi. Bạn xem lại nhé.

Muốn tính diện tích tích hình bình hành, ta lấy: Đáy x Chiều cao

Công thức: \(S=\dfrac{a.h}{2}\) (a là đáy, h là chiều cao)

Đáy × chiều cao 

Lời giải:

$A=2^0-2^1+2^2-2^3+2^4-...-2^{99}+2^{100}$

$2A=2^1-2^2+2^3-2^4+2^5-...-2^{100}+2^{101}$

$\Rightarrow A+2A=2^{101}-2^0$

$\Rightarrow 3A=2^{101}-1$

$\Rightarrow A=\frac{2^{101}-1}{3}$

tổng hai độ dài đáy nhân chiều cao chia cho hai

Chu vi hình thang = Đáy lớn + Đáy bé x chiều cao : 2

a) \(A=-x\left(x-2\right)+2x-8=-x^2+2x+2x-8\\ =-x^2+4x-8\\ =-\left(x^2-4x+4\right)+4-8\\ =-\left(x-2\right)^2-4\)

Vì : \(\left(x-2\right)^2\ge0\forall x\)

\(=>-\left(x-2\right)^2\le0\)

\(=>A\le-4\)

Dấu = xảy ra khi : \(\left(x-2\right)^2=0=>x=2\)

Vậy GTLN bt A là : -4 tại x = 2

b) \(B=-x^2+6x-11\\ =-\left(x^2-6x+9\right)+9-11\\ =-\left(x-3\right)^2-2\le-2\forall x\)

Dấu = xảy ra khi : \(\left(x-3\right)^2=0=>x=3\)

Vậy GTLN của B là : -2 tại x = 3

Bài 5:

Với $x,y$ là số nguyên thì $x+1, xy-1$ cũng là số nguyên. Mà tích của chúng bằng 3 nên ta có các TH sau:

TH1: $x+1=1, xy-1=3\Rightarrow x=0; xy=3$ (vô lý - loại) 

TH2: $x+1=-1, xy-1=-3\Rightarrow x=-2; xy=-2\Rightarrow y=1$ (thỏa mãn) 

TH3: $x+1=3; xy-1=1\Rightarrow x=2; xy=2\Rightarrow y=1$ (thỏa mãn)

TH4: $x+1=-3; xy-1=-1\Rightarrow x=-4; xy=0$ (vô lý -loại)

Vậy......

Bài 6:

$\frac{a}{7}-\frac{1}{2}=\frac{1}{b+3}$

$\Rightarrow \frac{2a-7}{14}=\frac{1}{b+3}$

$\Rightarrow (2a-7)(b+3)=14$

Với $a,b$ nguyên thì $2a-7, b+3$ cũng là số nguyên. Mà $(2a-7)(b+3)=14$ và $2a-7$ là số nguyên lẻ nên ta các TH sau:

TH1: $2a-7=1; b+3=14\Rightarrow a=4; b=11$ (thỏa mãn) 

TH2: $2a-7=-1; b+3=-14\Rightarrow a=3; b=-17$ (thỏa mãn) 

TH3: $2a-7=7; b+3=2\Rightarrow a=7; b=-1$ (thỏa mãn) 

TH4: $2a-7=-7; b+3=-2\Rightarrow a=0; b=-5$ (thỏa mãn)