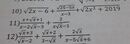Giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a,Sửa đề : \(\left(\frac{\sqrt{x}}{3+\sqrt{x}}+\frac{x+9}{9-x}\right):\left(\frac{3\sqrt{x}+1}{x-3\sqrt{x}}-\frac{1}{\sqrt{x}}\right)\)
\(=\left[\frac{\sqrt{x}}{3+\sqrt{x}}+\frac{x+9}{\left(3-\sqrt{x}\right).\left(3+\sqrt{x}\right)}\right]:\left[\frac{3\sqrt{x}+1}{\sqrt{x}.\left(\sqrt{x}-3\right)}-\frac{\sqrt{x}-3}{\sqrt{x}.\left(\sqrt{x}-3\right)}\right]\)
\(=\frac{\sqrt{x}.\left(3-\sqrt{x}\right)+x+9}{\left(3+\sqrt{x}\right).\left(3-\sqrt{x}\right)}:\frac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}.\left(\sqrt{x}-3\right)}\)
\(=\frac{\sqrt{x}.\left(3-\sqrt{x}\right)+x+9}{\left(3+\sqrt{x}\right).\left(3-\sqrt{x}\right)}.\frac{\sqrt{x}.\left(\sqrt{x}-3\right)}{2\sqrt{x}+4}\)
\(=\frac{\left[\sqrt{x}.\left(3-\sqrt{x}\right)+x+9\right].\sqrt{x}}{-\left(3+\sqrt{x}\right).\left(2\sqrt{x}+4\right)}=\frac{\left(3\sqrt{x}+9\right).\sqrt{x}}{-\left(3+\sqrt{x}\right).\left(2\sqrt{x}+4\right)}=\frac{-3\sqrt{x}}{2\sqrt{x}+4}\)
b, Với \(C< -1\)ta có : \(\frac{-3\sqrt{x}}{2\sqrt{x}+4}< -1\Leftrightarrow\frac{-3\sqrt{x}}{2\sqrt{x}+4}+1< 0\)
\(\Leftrightarrow\frac{-3\sqrt{x}+2\sqrt{x}+4}{2\sqrt{x}+4}< 0\Leftrightarrow\frac{4-\sqrt{x}}{2\sqrt{x}+4}< 0\)
Vì x > 0 nên \(\sqrt{x}>0\)khi đó : \(2\sqrt{x}+4>0\)
\(\Rightarrow4-\sqrt{x}< 0\Leftrightarrow\sqrt{x}>4\Leftrightarrow x>16\)
Vậy với \(x>16\)thì \(C< -1\)


Để hàm ssoo đã cho là hàm số bậc nhất thì
| a | \(\frac{m}{2}\ne0\Leftrightarrow m\ne0\) |
| b | \(3m+1\ne0\Leftrightarrow m\ne-\frac{1}{3}\) |
| c | \(\hept{\begin{cases}\sqrt{5-m}\ne0\\5-m\ge0\end{cases}\Leftrightarrow m< 5}\) |

hàm số đồng biến khi x tăng thì y tăng
ta xét với mọi \(x_1< x_2\) ta có :
\(\Rightarrow y_1=2x_1-3< 2x_2-3=y_2\)
vậy hàm số đã cho đồng biến trên R