Đây là toán nâng cao chuyên đề hai tỉ số trong đó có một đại lượng không đổi. Cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

                               Giải:

Vì người ta thêm vào hai ngăn mỗi ngăn 40 quyển nên hiệu số sách hai ngăn không đổi.

Số sách ngăn một lúc đầu là:

         7 : (7 - 3) = \(\dfrac{7}{4}\) ( hiệu số sách hai ngăn)

Số sách ngăn một lúc sau là:

        29 : (29 - 17) = \(\dfrac{29}{12}\)

Phân số chỉ 40 quyển sách là:

     \(\dfrac{29}{12}\) - \(\dfrac{7}{4}\)  = \(\dfrac{2}{3}\) (hiệu số sách hai ngăn)

Hiệu số sách hai ngăn là:

       40 ; \(\dfrac{2}{3}\) = 60 (quyển)

Số sách ngăn một lúc đầu là:

       60 x \(\dfrac{7}{4}\) = 105 (quyển)

Số sách ngăn hai lúc đầu là:

       105 - 60 = 45 (quyển)

Tổng số sách hai ngăn lúc sau khi chuyển là:

     105 + 45 + 40 x 2 = 230 (quyển)

Đáp số: 230 quyển. 

   Olm chào em, hiện tại câu hỏi của em chưa hiển thị đấy có thể là do file mà em tải lên bị lỗi nên đã không hiển thị trên diễn đàn. Em nên viết đề bài trực tiếp trên Olm. Như vậy em sẽ không mắc phải lỗi file đề như vậy. Điều này giúp em nhanh chóng nhận được sự trợ giúp từ cộng đồng olm. Cảm ơn em đã đồng hành cùng Olm.

Giá 5 hộp bút là: 

`5 xx 35 = 175` (nghìn đồng)

Giá 6 gói bim bim là: 

`6 xx 10 = 60 ` (nghìn đồng) 

Giá 9 kẹo mút là: 

`9 xx 3 = 27` (nghìn đồng)

Cô phải trả số tiền là: 

`175 + 60 + 27 = 262` (nghìn đồng)

Đáp số: ....

Nếu đề là \(\left(\dfrac{a+b}{b+c}+\dfrac{b-c}{b-a}\right).\dfrac{a-2b+3c}{a+c}\) thì có đúng đâu em

Em cứ thay thử \(a=1;b=2,c=\sqrt{3}\) thỏa mãn \(a^2+2b^2=3c^2\) vào biểu thức là thấy

Kết quả ko phải 1 số nguyên dương

nhưng c có thể bằng \(-\sqrt{3}\) mà

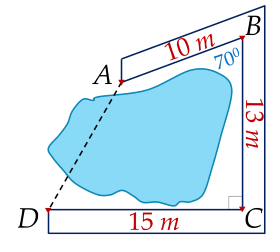
`DE = DB . sinB = 10. sin70^o ~~ 9,4 (m) `

`=> AF ~~ 15 - 9,4~~ 5,6 (m) `

`ΔAFD` vuông tại `F `

`=> AD = sqrt{AF^2 + DF^2} = sqrt{AF^2 + EC^2} = sqrt{5,6^2 + 13^2} ~~14,15 (m)`

Vậy ....

Cho A = (10⁷ + 10⁸ + 10⁹)

CM A : 222

Ta có: A = 10⁷ + 10⁸ + 10⁹

          A = 10⁷.(1 + 10 + 10²)

           A = 10⁷.(1 + 10 + 100)

           A = 10⁷.(11 + 100)

          A  =10⁷.111

         A = 10.10⁶.111

         A = 2.5.10⁶.111

         A = (2.111).5.10⁶

        A = 222.5.10⁶ ⋮ 222 (đpcm)

a) Nhiệt độ t (⁰C) tuần tới tại Tokyo là:

t > -5

b) Gọi x (tuổi) là tuổi của người điều khiển xe máy điện. Ta có bất đẳng thức:

x ≥ 16

c) Gọi z (đồng) là mức lương tối thiểu trong một giờ làm việc của người lao động. Ta có bất đẳng thức:

z ≥ 20000

d) y là số dương nên ta có bất đẳng thức:

y > 0

a, t>5

b,x≥16

c,mức lương tối thiểu≤20 000đ

d, y>0

a) ĐKXĐ: x ≠ -5

Phương trình đã cho trở thành:

(x + 6).2 + 3.(x + 5) = 2.2(x + 5)

2x + 12 + 3x + 15 = 4x + 20

5x - 4x = 20 - 12 - 15

x = -7 (nhận)

Vậy S = {-7}

b) x + 3y = -2

x = -2 - 3y (1)

5x + 8y = 11 (2)

Thế (1) vào (2), ta được:

5(-2 - 3y) + 8y = 11

-10 - 15y + 8y = 11

-7y = 11 + 10

-7y = 21

y = 21 : (-7)

y = -3

Thế y = -3 vào (1), ta được:

x = -2 - 3.(-3) = 7

Vậy S = {(7; -3)}

Gọi vận tốc lúc về của người đó là x(km/h)

(Điều kiện: x>0)

Vận tốc lúc đi là x+10(km/h)

Thời gian người đó đi từ A đến B là \(\dfrac{60}{x+10}\left(giờ\right)\)

Thời gian người đó đi từ B về A là \(\dfrac{60}{x}\left(giờ\right)\)

Thời gian về nhiều hơn thời gian đi là 30p=0,5 giờ nên ta có:

\(\dfrac{60}{x}-\dfrac{60}{x+10}=0,5\)

=>\(\dfrac{60x+600-60x}{x\left(x+10\right)}=0,5\)

=>\(x\left(x+10\right)=\dfrac{600}{0,5}=1200\)

=>\(x^2+10x-1200=0\)

=>(x+40)(x-30)=0

=>\(\left[{}\begin{matrix}x+40=0\\x-30=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-40\left(loại\right)\\x=30\left(nhận\right)\end{matrix}\right.\)

Vậy: Vận tốc lúc về của người đó là 30km/h

1) sin35⁰ = cos(90⁰ - 35⁰) = cos55⁰

Vậy sin35⁰ = cos55⁰

tan35⁰ = cot(90⁰ - 35⁰) = cot55⁰

Vậy tan35⁰ = cot55⁰

2) ∆ABC vuông tại A (gt)

⇒ AB = BC.cosB

= 20.cos36⁰

≈ 16,18 (cm)