
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Vì $ƯCLN(a,b)=21$ nên đặt $a=21x, b=21y$ với $x,y$ là stn, $x,y$ nguyên tố cùng nhau.
Ta có:
$BCNN(a,b)=21xy=420\Rightarrow xy=20$ (1)
$a+21=b$
$\Rightarrow 21x+21=21y$
$\Rightarrow x+1=y$ (2)
Từ $(1); (2)$ và $x,y$ là 2 số nguyên tố cùng nhau nên $x=4, y=5$
$\Rightarrow a=21x=21.4=84; b=21y=21.5=105$


Lời giải:
Gọi $d=ƯCLN(2n+5, 8n+24)$
$\Rightarrow 2n+5\vdots d; 8n+24\vdots d$
$\Rightarrow 8n+24-4(2n+5)\vdots d$
$\Rightarrow 4\vdots d$ (1)
Vì $2n+5\vdots d$, mà $2n+5$ lẻ nên $d$ lẻ (2)
Từ $(1); (2)\Rightarrow d=1$
$\Rightarrow 2n+5, 8n+24$ nguyên tố cùng nhau.
$\Rightarrow BCNN(2n+5, 8n+24)=(2n+5)(8n+24)$

Lời giải:
Đặt $6a+4=2^m, a+2=2^n$ với $m,n$ là số tự nhiên, $m>n$
$\Rightarrow 6.2^n-2^m=8$
$2^{n+1}(3-2^{m-n-1})=8$
$2^n(3-2^{m-n-1})=4$
$\Rightarrow 2^n$ là ước của 4.
$\Rightarrow n=0,1,2$
Nếu $n=0$ thì: $3-2^{m-1}=4\Rightarrow 2^{m-1}=-1$ (loại)
Nếu $n=1$ thì: $a+2=2^1=2\Rightarrow a=0$ (loại do $a$ nguyên dương)
Nếu $n=2$ thì $a+2=2^2=4\Rightarrow a=2$ (tm)

Tích của 6 số bất kì là 1 số âm thì nhiều nhất là 5 số dương và 1 số âm.
Bỏ 1 số âm đó đi ta được 78 số nguyên vậy ta chia được 13 cặp số có tích là một số âm.
⇒ Tích của 13 cặp là số nguyên âm.
Mà ở đây ta lại có thêm một số nguyên âm ⇒ Vậy nên tích của 79 số đó là số dương (ĐPCM)

Lời giải:
** Bổ sung điều kiện $x,y$ là các số nguyên.
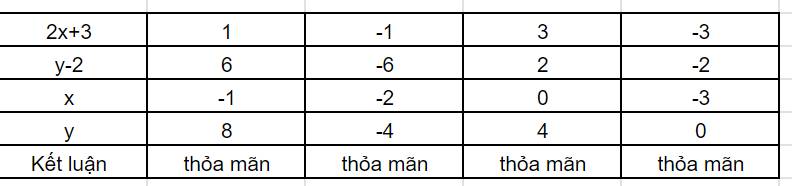
Với $x,y$ nguyên thì $y-2, 2x+3$ cũng là số nguyên.
Mà $(y-2)(2x+3)=6$ và $2x+3$ là số nguyên lẻ nên ta có bảng sau:

722\(x-6\) = 49
Nếu 2\(x\) - 6 ≤ 0 thì 720 ≤ 1 < 49 (loại)
Nếu 2\(x\) - 6 ≥ 0 ⇒ 72\(^{2x-6}\) là số chẵn ≠ 49 là số lẻ (loại)
Vậy không có giá trị nguyên nào của \(x\) thỏa mãn đề bài

Lời giải:
$3xy-2x+5y=9$
$x(3y-2)+5y=9$
$3x(3y-2)+15y=27$
$3x(3y-2)+5(3y-2)=17$
$(3x+5)(3y-2)=17$
Do $x,y$ nguyên nên $3x+5, 3y-2$ cũng là số nguyên. Ta có bảng sau: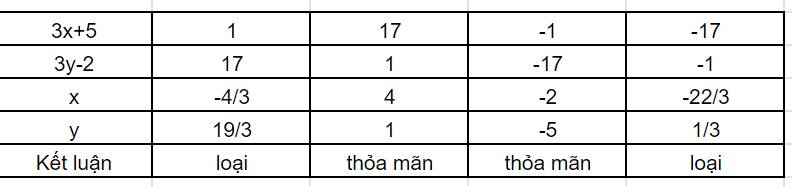
1.
Giả sử cửa hàng huy động được a xe 5 tấn và b xe 3 tấn.
$5a+3b=25$
$3b=25-5a\vdots 5\Rightarrow b\vdots 5$
$3b=25-5a< 25$ do $a>0$
$\Rightarrow b< 8,3...$
Mà $b\vdots 5$ và $b>0$ nên $b=5$
Khi đó: $a=\frac{25-3b}{5}=\frac{25-3.5}{5}=2$
Vậy có 2 xe 5 tấn và 5 xe 3 tấn.
2.
Do $ƯCLN(a,b)=20$ nên đặt $a=20x, b=20y$ với $x,y$ là số tự nhiên, $x,y$ nguyên tố cùng nhau.
Do $a> b$ nên $x>y$.
$a+b=140$
$\Rightarrow 20x+20y=140$
$\Rightarrow x+y=140:20=7$
Mà $x,y$ nguyên tố cùng nhau và $x> y$ nên $x=7, y=1$ hoặc $x=5, y=2$
$\Rightarrow (a,b)=(140, 20), (100, 40)$