Cho tam giác ABC cân tại A . Trên cạnh AB lấy điểm D , trên tia đối của tia CA lấy điểm E sao cho BD = CE . Qua D và E kẻ các đường thẳng vuông góc với BC lần lượt tại M và N . a) Chứng minh rằng: BM = CN . b) Gọi I là giao điểm của BC và DE . Chứng minh DE =2ID. c) Kẻ AH vuông góc với BC tại H . Đường thẳng đi qua I và vuông góc với DE cắt AH tại K . Tính số đo góc DBK.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
B4: Cho tam giác ABC = tam giác MNP. Biết AB+BC=7cm;MN-NP=3cm;MP=4cm. Tính các cạnh của hai tam giác


xét hai tam giác ABH và ACH (H= 90') ta có: góc B = C : AC=AB => tam giác ABH=ACH ( cạnh nên BH=HC ( cặp cạnh tương ứng) xét hai tam giác BEH (E= 90') và CDH (D= 90') ta có: BH = CH : góc B=C => tam giác BEH=CDH
bạn ơi mik cần chứng minh song song, chứ ko phải chứng minh tam giác ;-;

a)
Theo đề ra: \(x\) và \(y\) hai đại lượng tỉ lệ thuận nên:
\(y=k.x\left(k\ne0\right)\)
\(\Rightarrow40=k.8\)
\(\Rightarrow k=5\)
Vậy hệ số tỉ lệ \(k\) của \(y\) đối với \(x\) là 5.
b)
\(y=5.x\)
c)
Trường hợp 1: \(x=20\)
\(\Rightarrow y=5.20=100\)
Trường hợp 2: \(x=5\)
\(\Rightarrow y=4.5=20\).

b)Theo đề bài,ta có:
\(\dfrac{2x}{3y}=-\dfrac{1}{3}\)
\(\Rightarrow-6x=3y\)
\(\Rightarrow\dfrac{x}{3}=-\dfrac{y}{6}=\dfrac{2x}{6}=-\dfrac{3y}{18}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{2x}{6}=-\dfrac{3y}{18}=\dfrac{2x+3y}{6+\left(-18\right)}=\dfrac{7}{12}\)
\(\Rightarrow x=\dfrac{7}{12}\cdot3=\dfrac{7}{4}\)
\(y=\dfrac{7}{12}\cdot-6=-\dfrac{7}{2}\)

a) Đề là chứng minh \(\dfrac{a^2+c^2}{b^2+c^2}=\dfrac{a}{b}\) à bạn?
Ta có: \(\dfrac{a}{c}=\dfrac{c}{b}\)
\(\Rightarrow ab=c^2\)
\(\Rightarrow\dfrac{a^2+c^2}{b^2+c^2}=\dfrac{a^2+ab}{b^2+ab}=\dfrac{a\left(a+b\right)}{b\left(a+b\right)}=\dfrac{a}{b}\)
\(\Rightarrowđpcm\)
b)
Ta có: \(\dfrac{a}{c}=\dfrac{c}{d}\)
\(\Rightarrow c^2=ab\)
\(\Rightarrow\dfrac{b^2-a^2}{a^2+c^2}=\dfrac{b^2-a^2}{a^2+ab}=\dfrac{\left(b-a\right)\left(b+a\right)}{a\left(a+b\right)}=\dfrac{b-a}{a}\)
\(\Rightarrowđpcm.\)
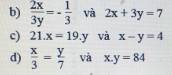
giúp tớ vớii