a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)

a) xét tam giác AOB và tam giác COD, ta có :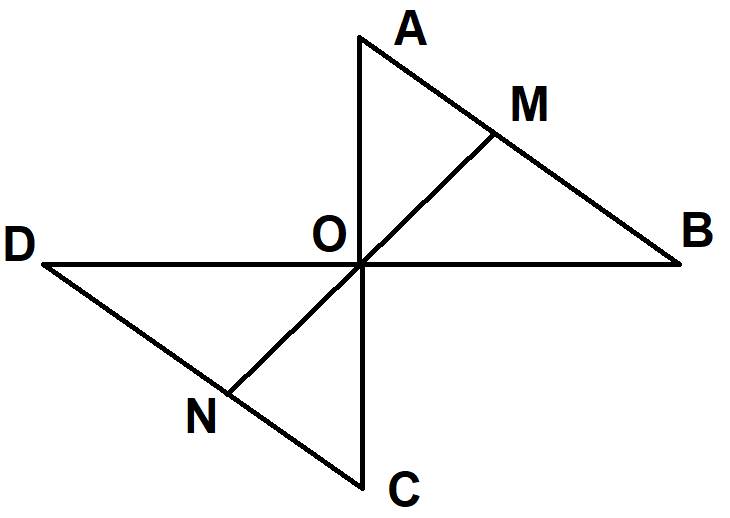
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)

\(4^x-5+4^x-3=68\\ \Rightarrow4^x+4^x-5-3=68\\ \Leftrightarrow2\times4^x-5-3=68\\ \Rightarrow2\times4^x-8=68\\ 2\times4^x=68+8\\ 2\times4^x=76\\ \Rightarrow\dfrac{2\times4^x}{2}=\dfrac{76}{2}=38\\ \Leftrightarrow x=\dfrac{In\left(38\right)}{2In\left(2\right)}\)

\(4^{x-5}+4^{x-3}=68\)

\(\dfrac{4^x}{1024}+\dfrac{4^x}{64}=68\)

\(\dfrac{17.4^x}{1024}=68\)

\(17.4^{x-5}=68\)

\(4^{x-5}=4\)

\(x-5=1\)

\(x=6\)

Bổ sung điều kiện $x$ nguyên

Lời giải:

Ta có:

\(C=\frac{x^2+1}{x-1}=\frac{x(x-1)+(x-1)+2}{x-1}=x+1+\frac{2}{x-1}\)

Với $x$ nguyên, để $C$ nguyên thì $\frac{2}{x-1}$ phải là số nguyên. 

Điều này xảy ra khi $x-1$ là ước của $2$

$\Rightarrow x-1\in\left\{1; -1; 2;-2\right\}$

$\Rightarrow x\in\left\{2; 0; 3; -1\right\}$

Câu 1:

ΔABC có:

AB = AC; góc B = 60°(theo bài ra)

⇒ΔABC là tam giác đều

Câu 2: Muốn so sanh các dữ liệu, ta nên dùng biểu đồ hình quạt tròn là hợp lí nhất.

Câu 3:

a) -Số trận thắng của đội bóng thuộc dữ liệu số.

- Từ năm 2017 đến năm 2020 số trận thắng có xu hướng tăng.

b)

                                          \(Bài\text{ }giải\)

                \(a.Giá\text{ }của\text{ }mỗi\text{ }chiếc\text{ }tivi\text{ }trong\text{ }tháng\text{ }9\text{ }là:\)

               \(80000000-8000000\cdot5\%=7600000\left(đồng\right)\)

\(b.Giá\text{ }của\text{ }mỗi\text{ }chiếc\text{ }tivi\text{ }trong\text{ }tháng\text{ }10\text{ }ít\text{ }hơn\text{ }trong\text{ }tháng\text{ }9\text{ }là:\)

                    \(7600000-6840000=760000\left(đồng\right)\)

\(Tháng\text{ }10,\text{ }siêu\text{ }thị\text{ }đã\text{ }giảm\text{ }giá\text{ }số\text{ }phần\text{ }trăm\text{ }cho\text{ }một\text{ }chiếc\text{ }tivi\text{ }so\text{ }với\text{ }tháng\text{ }9\text{ }là:\)

                          \(7600000:760000=10\%\)

\(\dfrac{a}{2016}=\dfrac{b}{2017}=\dfrac{c}{2018}=\dfrac{a-c}{2016-2018}=\dfrac{a-b}{2016-2017}=\dfrac{b-c}{2017-2018}\)

\(\rightarrow\dfrac{a-c}{-2}=\dfrac{a-b}{-1}=\dfrac{b-c}{-1}\)

\(\rightarrow a-c=2\cdot\left(a-b\right)=2\cdot\left(b-c\right)\)

\(\rightarrow\left(a-c\right)^3=\left[2\cdot\left(a-b\right)\right]^2\cdot2\cdot\left(b-c\right)\)

\(\Rightarrow\left(a-c\right)^3=8\cdot\left(a-b\right)^2\cdot\left(b-c\right)\)

\(3x=2y=>y=\dfrac{3}{2}x\)

Thay \(y=\dfrac{3}{2}x;z=3x\) vào `x+y+z=99` có:

    \(x+\dfrac{3}{2}x+3x=99=>x=18\)

\(=>\)$\begin{cases} y=\dfrac{3}{2}.18=27\\z=3.18=54 \end{cases}$