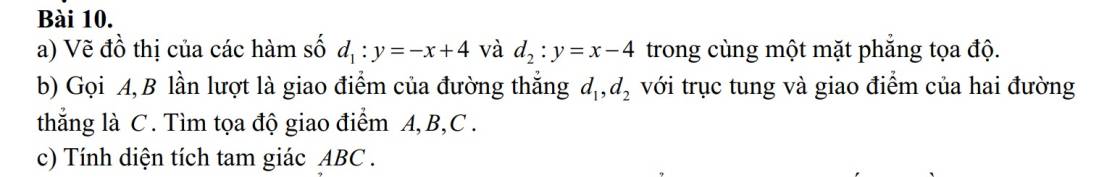
help me !!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xác suất thực nghiệm của biến cố "Thẻ lấy ra ghi số 7" là:
\(\dfrac{6}{30}=\dfrac{1}{5}\)
b: Gọi A là biến cố "Thẻ rút ra là số nguyên tố"
=>A={2;3;5;7;11;13}
=>n(A)=6
=>\(P_A=\dfrac{6}{15}=\dfrac{2}{5}\)
=>Khi số lần rút thẻ ngày càng lớn thì xác suất thực nghiệm của biến cố A ngày càng gần với 2/5

a: \(x^2+5x+\dfrac{25}{4}=x^2+2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2=\left(x+\dfrac{5}{2}\right)^2\)
b: \(16x^2-8x+1=\left(4x\right)^2-2\cdot4x\cdot1+1^2=\left(4x-1\right)^2\)
c: \(4x^2+12xy+9y^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2=\left(2x+3y\right)^2\)
d: \(\left(x+3\right)\left(x+4\right)\left(x+5\right)\left(x+6\right)+1\)
\(=\left(x^2+9x+18\right)\left(x^2+9x+20\right)+1\)
\(=\left(x^2+9x\right)^2+38\left(x^2+9x\right)+360+1\)
\(=\left(x^2+9x\right)^2+2\cdot\left(x^2+9x\right)\cdot19+19^2\)
\(=\left(x^2+9x+19\right)^2\)

1: Xét ΔDIN vuông tại I và ΔDKP vuông tại K có
\(\widehat{IDN}=\widehat{KDP}\)(hai góc đối đỉnh)
Do đó: ΔDIN~ΔDKP
2: Xét ΔMIN vuông tại I và ΔMKP vuông tại K có
\(\widehat{IMN}=\widehat{KMP}\)
Do đó: ΔMIN~ΔMKP
=>\(\dfrac{MI}{MK}=\dfrac{MN}{MP}\)
=>\(MI\cdot MP=MN\cdot MK\)

\(\dfrac{\left(x-2\right)^2}{3}-\dfrac{\left(2x-3\right)\left(2x+3\right)}{8}+\dfrac{\left(x-4\right)^2}{6}=0\)
=>\(\dfrac{8\left(x-2\right)^2-3\left(2x-3\right)\left(2x+3\right)+4\left(x-4\right)^2}{24}=0\)
=>\(8\left(x^2-4x+4\right)-3\left(4x^2-9\right)+4\left(x^2-8x+16\right)=0\)
=>\(8x^2-32x+32-12x^2+27+4x^2-32x+64=0\)
=>-64x+123=0
=>\(x=\dfrac{123}{64}\)

a: (2m-4)x+2-m=0
=>x(2m-4)=m-2
TH1: m=2
Phương trình sẽ trở thành \(x\left(2\cdot2-4\right)=2-2\)
=>0x=0(luôn đúng)
=>Phương trình có vô số nghiệm
TH2: \(m\ne2\)
Phương trình sẽ tương đương với \(x=\dfrac{m-2}{2m-4}=\dfrac{1}{2}\)
b: \(\left(m+1\right)x=\left(3m^2-1\right)x+m-1\)
=>\(\left(m+1\right)x-\left(3m^2-1\right)x=m-1\)
=>\(x\left(m+1-3m^2+1\right)=m-1\)
=>\(x\left(-3m^2+m+2\right)=m-1\)
=>\(x\left(-3m^2+3m-2m+2\right)=m-1\)
=>\(x\cdot\left(m-1\right)\left(-3m-2\right)=m-1\)
TH1: m=1
Phương trình sẽ trở thành \(x\left(1-1\right)\left(-3\cdot1-2\right)=1-1\)
=>0x=0(luôn đúng)
=>Phương trình có vô số nghiệm
TH2: m=-2/3
Phương trình sẽ trở thành:
\(x\left(-\dfrac{2}{3}-1\right)\left(-3\cdot\dfrac{-2}{3}-2\right)=\dfrac{-2}{3}-1\)
=>0x=-5/3(vô lý)
=>Phương trình vô nghiệm
TH3: \(m\notin\left\{1;-\dfrac{2}{3}\right\}\)
Phương trình sẽ tương đương với \(x=\dfrac{m-1}{\left(m-1\right)\left(-3m-2\right)}=\dfrac{-1}{3m+2}\)
c: \(ax+2m=a+x\)
=>ax-x=a-2m
=>x(a-1)=a-2m
TH1: a=1
Phương trình sẽ trở thành:
x(1-1)=1-2m
=>0x=1-2m
-Nếu \(m=\dfrac{1}{2}\) thì 0x=1-2*1/2=0
=>Phương trình có vô số nghiệm
Nếu \(m\ne\dfrac{1}{2}\) thì phương trình vô nghiệm
TH2: a<>1
Phương trình sẽ tương đương với \(x=\dfrac{a-2m}{a-1}\)

a: \(3x+\left(-5+x\right)=7-\left(5x-4\right)\)
=>3x-5+x=7-5x+4
=>4x-5=-5x+11
=>9x=16
=>\(x=\dfrac{16}{9}\)
b: Đề thiếu vế phải rồi bạn
c: \(2\left(x+5\right)-9x=12-4\left(2x-3\right)\)
=>2x+10-9x=12-8x+12
=>-7x+10=-8x+24
=>-7x+8x=24-10
=>x=14
d: \(x-\left(3x+1\right)=-\left(x+1\right)+21\)
=>x-3x-1=-x-1+21
=>-2x-1=-x+20
=>-2x+x=20+1
=>-x=21
=>x=-21

Lời giải:
Gọi đa thức trên là $A$
$A=a^2b^2(a-b)-b^2c^2[(a-b)+(c-a)]+a^2c^2(c-a)$
$=a^2b^2(a-b)-b^2c^2(a-b)+a^2c^2(c-a)-b^2c^2(c-a)$
$=(a-b)(a^2b^2-b^2c^2)+(c-a)(a^2c^2-b^2c^2)$
$=(a-b)b^2(a^2-c^2)+(c-a)c^2(a^2-b^2)$
$=(a-b)b^2(a-c)(a+c)+(c-a)c^2(a-b)(a+b)$
$=(a-b)(a-c)[b^2(a+c)-c^2(a+b)]$
$=(a-b)(a-c)(b^2a+b^2c-ac^2-bc^2)$
$=(a-b)(a-c)[a(b^2-c^2)+bc(b-c)]$
$=(a-b)(a-c)(b-c)(ab+bc+ac)$
Lần sau bạn lưu ý, gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.
a)
b) Hàm số y=-x+4 cắt Oy tại \(\left(0;4\right)\) \(\Rightarrow A\left(0;4\right)\)
Hàm số y=x-4 cắt Oy tại \(\left(0;-4\right)\) \(\Rightarrow B\left(0;-4\right)\)
Ta có pt hoành độ giao điểm của y=-x+4 và y=x-4 là:
\(-x+4=x-4\Leftrightarrow x=4\)
\(\Rightarrow y=4-4=0\)
\(\Rightarrow C\left(4;0\right)\)
c) Ta có: \(A\left(0;4\right)\Rightarrow OA=4\)
\(B\left(0;-4\right)\Rightarrow OB=4\)
\(C\left(0;4\right)\Rightarrow OC=4\)
BC = OA + OB = 4 + 4 = 8
\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot4\cdot8=16\) (đvdt)