chiều nay mik phải nộp r cứu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: \(\widehat{xBy}=\widehat{xAz}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên By//Az
b: Ta có: \(\widehat{ABC}+\widehat{xBC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABC}+60^0=180^0\)
=>\(\widehat{ABC}=120^0\)
AC là phân giác của góc zAB
=>\(\widehat{BAC}=\dfrac{\widehat{xAB}}{2}=30^0\)
Xét ΔBAC có \(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^0\)
=>\(\widehat{BCA}+120^0+30^0=180^0\)
=>\(\widehat{BCA}=30^0\)
c: Ta có: BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=60^0\)
Xét ΔDBA có \(\widehat{DBA}+\widehat{DAB}=60^0+30^0=90^0\)
nên ΔBDA vuông tại D
=>BD\(\perp\)AC

AE//BD
=>\(\widehat{BAE}+\widehat{ABD}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{BAE}+90^0=180^0\)
=>\(\widehat{BAE}=90^0\)
Ta có: AE//BD
=>\(\widehat{AED}+\widehat{BDE}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{BDE}+55^0=180^0\)
=>\(\widehat{BDE}=125^0\)

a: a\(\perp\)HK
b\(\perp\)HK
Do đó: a//b
b: Ta có: \(\widehat{BAH}+45^0=180^0\)
=>\(\widehat{BAH}=180^0-45^0=135^0\)
Ta có: a//b
=>\(\widehat{BAH}+\widehat{ABK}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{ABK}+135^0=180^0\)
=>\(\widehat{ABK}=45^0\)

Số phần quả bóng còn lại so với tổng số bóng ban đầu là:
\(1-\dfrac{1}{7}-\dfrac{1}{5}=1-\dfrac{12}{35}=\dfrac{23}{35}\)

\(\left(x-1\right)+\left(x-2\right)+...+\left(x-20\right)=150\\ x-1+x-2+...+x-20=150\\ \left(x+x+...+x\right)-\left(1+2+...+20\right)\\ 20\cdot x-\left[\left(20-1\right):1+1\right]\cdot\left(20+1\right):2=150\\ 20\cdot x-20\cdot21:2=150\\ 20\cdot x-210=150\\ 20\cdot x=150+210\\ 20\cdot x=360\\ x=360:20\\ x=18\)

Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}ab\cdot sinC=\dfrac{1}{2}\cdot7\cdot23\cdot sin130^o=61,7\) (đvdt)

Bài 14:
Số bao đường ở mỗi kho ban đầu là:
168:3=56(bao)
Số bao đường ở mỗi kho sau đó là:
56+16=72(bao)
Số bao đường đã bán hết là:
72x2=144(bao)

a: Ta có: \(\widehat{xOy}=\widehat{mOn}\)(hai góc đối đỉnh)
mà \(\widehat{xOy}=50^0\)
nên \(\widehat{mOn}=50^0\)
Ta có: \(\widehat{xOy}+\widehat{mOy}=180^0\)(hai góc kề bù)
=>\(\widehat{mOy}+50^0=180^0\)
=>\(\widehat{mOy}=130^0\)
Ta có: \(\widehat{xOn}=\widehat{mOy}\)(hai góc đối đỉnh)
mà \(\widehat{mOy}=130^0\)
nên \(\widehat{xOn}=130^0\)
b: Oa là phân giác của góc xOy
=>\(\widehat{yOa}=\dfrac{\widehat{xOy}}{2}=25^0\)
Ta có: Ob là phân giác của góc yOm
=>\(\widehat{yOb}=\dfrac{\widehat{yOm}}{2}=65^0\)
Ta có: \(\widehat{aOb}=\widehat{aOy}+\widehat{bOy}=25^0+65^0=90^0\)
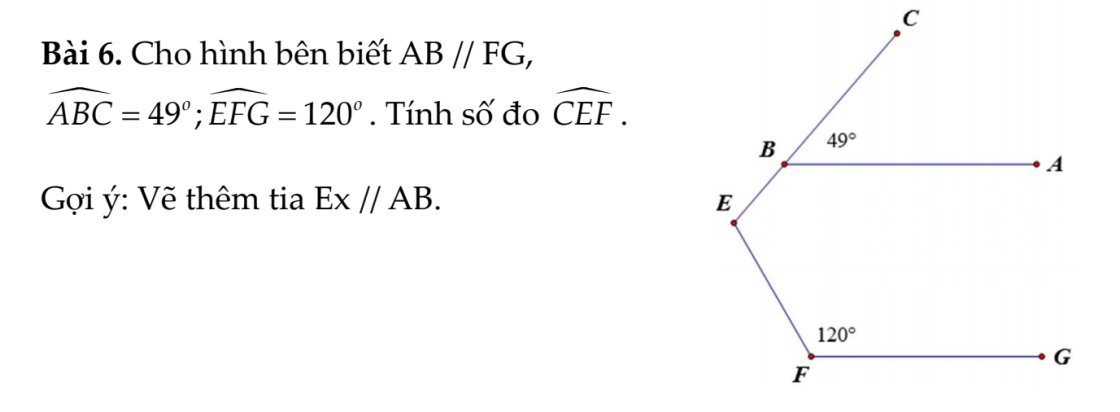
Kẻ Ex//AB(Ex và AB nằm trên cùng mặt phẳng bờ chứa tia BE)
Ta có: Ex//AB
AB//FG
Do đó: Ex//FG
Ex//AB
=>\(\widehat{BEx}=\widehat{CBA}\)(hai góc đồng vị)
=>\(\widehat{xEB}=49^0\)
Ta có: Ex//FG
=>\(\widehat{xEF}+\widehat{EFG}=180^0\)
=>\(\widehat{xEF}=180^0-120^0=60^0\)
\(\widehat{BEF}=\widehat{xEB}+\widehat{xEF}=49^0+60^0=109^0\)