Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu chính xác biểu thức bạn viết nhé.

  Olm chào em, chúc mừng em đã biết vận dụng cách làm của diễn đàn vào các dạng toán tương tự khi đi thi để đạt kết quả cao. Chững tỏ chất lượng câu trả lời trên diễn đàn Olm là rất chuẩn em nhỉ.

1: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có

\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)

Do đó: ΔHFB~ΔHEC

=>\(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)

=>\(\dfrac{HF}{HB}=\dfrac{HE}{HC}\)

=>\(HF\cdot HC=HB\cdot HE\)

2: Xét ΔHFE và ΔHBC có

\(\dfrac{HF}{HB}=\dfrac{HE}{HC}\)

\(\widehat{FHE}=\widehat{BHC}\)(hai góc đối đỉnh)

Do đó: ΔHFE~ΔHBC

=>\(\widehat{HFE}=\widehat{HBC}\)

3) Do \(\Delta HFE\sim\Delta HBC\) có các đường cao tương ứng là HK, HD nên \(\Delta HKF\sim\Delta HDB\)

 \(\Rightarrow\dfrac{FK}{BD}=\dfrac{HF}{HB}\)

Mà \(\dfrac{HF}{HB}=\dfrac{HF}{HC}\) (do \(\Delta HFE\sim\Delta HBC\)) nên \(\dfrac{FK}{BD}=\dfrac{HE}{HC}\) (đpcm)

Mặt khác, ta có \(\Delta HEK\sim\Delta HCD\) nên \(\dfrac{KE}{CD}=\dfrac{HE}{HC}\)

Từ đó \(\dfrac{FK}{BD}=\dfrac{KE}{CD}\) \(\Rightarrow\dfrac{FK}{KE}=\dfrac{BD}{DC}\)

Lại có KJ//EC nên \(\dfrac{FK}{KE}=\dfrac{FJ}{JC}\). Do đó \(\dfrac{BD}{DC}=\dfrac{FJ}{JC}\).

Áp dụng định lý Thales đảo \(\Rightarrow\) DJ//BF hay DJ//BA.

Mà \(CF\perp BA\) nên \(DJ\perp CF\) (đpcm)

1: Thay m=5 vào (d1), ta được:

\(y=\left(5-3\right)x-4=2x-4\)

Vẽ đồ thị

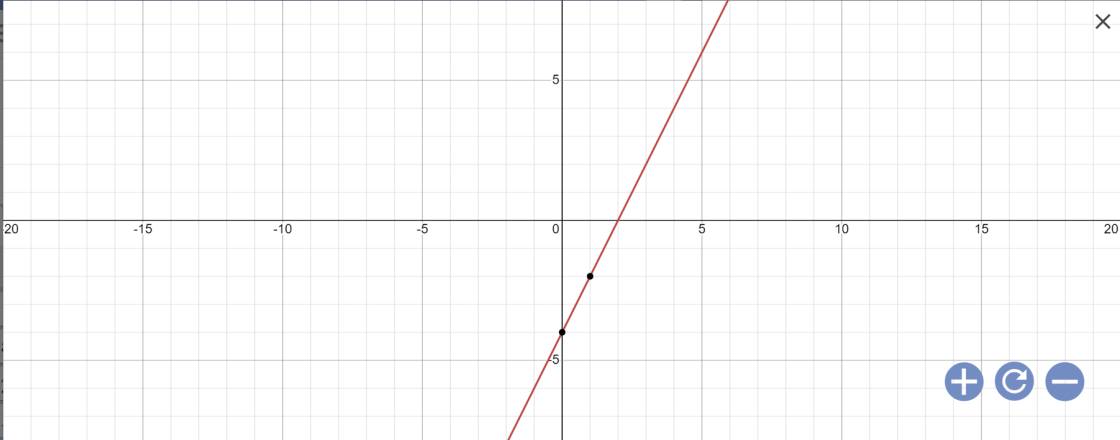
2: Tọa độ giao điểm của (d1) với trục Ox là:

\(\left\{{}\begin{matrix}y=0\\\left(m-3\right)x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{4}{m-3}\end{matrix}\right.\)

Để x<0 thì \(\dfrac{4}{m-3}< 0\)

=>m-3<0

=>m<3

mà m là số tự nhiên

nên \(m\in\left\{0;1;2\right\}\)

Gọi số sản phẩm đội đó phải hoàn thành theo kế hoạch là x(sản phẩm)

(Điều kiện: \(x\in Z^+\))

Số sản phẩm thực tế đội đó làm được là x+20(sản phẩm)

Thời gian dự kiến hoàn thành là \(\dfrac{x}{20}\left(ngày\right)\)

Thời gian thực tế hoàn thành là \(\dfrac{x+20}{30}\left(ngày\right)\)

Thực tế hoàn thành trước kế hoạch 2 ngày nên ta có:

\(\dfrac{x}{20}-\dfrac{x+20}{30}=2\)

=>\(\dfrac{3x-2\left(x+20\right)}{60}=2\)

=>x-40=120

=>x=160(nhận)

Vậy: Theo kế hoạch, đội phải hoàn thành 160 sản phẩm

1: Thay x=3 vào A, ta được:

\(A=\dfrac{2\cdot3}{3-1}=\dfrac{6}{2}=3\)

2: \(B=\dfrac{x}{x-1}-\dfrac{3}{x+1}-\dfrac{2}{x^2-1}\)

\(=\dfrac{x}{x-1}-\dfrac{3}{x+1}-\dfrac{2}{\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{x\left(x+1\right)-3\left(x-1\right)-2}{\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{x^2+x-3x+3-2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-2x+1}{\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{x+1}\)

3: \(A\cdot B=x\)

=>\(x=\dfrac{x-1}{x+1}\cdot\dfrac{2x}{x-1}=\dfrac{2x}{x+1}\)

=>\(x\left(x+1\right)=2x\)

=>\(x\left(x-1\right)=0\)

=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=1\left(loại\right)\end{matrix}\right.\)

Bạn có thể chụp hình rõ hơn không? Đề mờ quá.

Câu 1:

a: Khi x=3 thì \(A=\dfrac{3-6}{3+2}=\dfrac{-3}{5}\)

b: \(B=\dfrac{6}{x-2}+\dfrac{x}{x+2}-\dfrac{8}{x^2-4}\)

\(=\dfrac{6}{x-2}+\dfrac{x}{x+2}-\dfrac{8}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{6\left(x+2\right)+x\left(x-2\right)-8}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{6x+12+x^2-2x-8}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)

c: \(P=A\cdot B=\dfrac{x+2}{x-2}\cdot\dfrac{x-6}{x+2}=\dfrac{x-6}{x-2}\)

P=3/2

=>\(\dfrac{x-6}{x-2}=\dfrac{3}{2}\)

=>\(3\left(x-2\right)=2\left(x-6\right)\)

=>3x-6=2x-12

=>x=-6(nhận)

Câu 2:

a: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{18^2+24^2}=30\left(cm\right)\)

b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔBHA~ΔBAC

Câu 1

Gọi x (km) là độ dài quãng đường AB (x > 0)

Thời gian đi từ A đến B: x/40 (h)

Thời gian đi từ B về A: x/50 (h)

36 phút = 3/5 h

Theo đề bài, ta có phương trình:

x/40 + x/50 + 3/5 = 6

5x + 4x + 40.3 = 200.6

9x + 120 = 1200

9x = 1200 - 120

9x = 1080

x = 1080 : 9

x = 120 (nhận)

Vậy quãng đường AB dài 120 km

Câu 2. Em xem lại đề nhé

a: ΔABC vuông tại A

mà AD là đường trung tuyến

nên DA=DB=DC

ΔDAB có DA=DB

nên ΔDAB cân tại D

=>\(\widehat{DAB}=\widehat{DBA}\)

mà \(\widehat{DAB}+\widehat{DFA}=90^0\)(ΔDAF vuông tại D)

và \(\widehat{DBA}+\widehat{DCA}=90^0\)(ΔABC vuông tại A)

nên \(\widehat{DFA}=\widehat{DCA}\)

Xét ΔAEF vuông tại A và ΔABC vuông tại A có

\(\widehat{AFE}=\widehat{ACB}\)

Do đó: ΔAEF~ΔABC

b: Xét ΔDBF và ΔDEC có

\(\widehat{DFB}=\widehat{DCE}\)

\(\widehat{BDF}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó ΔDBF~ΔDEC

=>\(\dfrac{DB}{DE}=\dfrac{DF}{DC}\)

=>\(DB\cdot DC=DE\cdot DF\)

=>\(DC^2=DE\cdot DF\)

=))

Lời giải:
Áp dụng BĐT Cauchy có:

$\frac{a^3}{b}+ab\geq 2\sqrt{\frac{a^3}{b}.ab}=2a^2$

$\frac{b^3}{c}+bc\geq 2b^2$

$\frac{c^3}{a}+ac\geq 2c^2$

$\Rightarrow \frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}+ab+bc+ac\geq 2(a^2+b^2+c^2)(1)$

Cũng áp dụng BĐT Cauchy ta dễ thấy:
$a^2+b^2+c^2\geq ab+bc+ac(2)$

Từ $(1); (2)\Rightarrow \frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\geq 2(a^2+b^2+c^2)-(ab+bc+ac)\geq a^2+b^2+c^2+ab+bc+ac-(ab+bc+ac)=a^2+b^2+c^2$
Ta có đpcm

Dấu "=" xảy ra khi $a=b=c$

Lần sau bạn lưu ý gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu của bạn hơn nhé.