
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 11
\(x=3y\) và y = 5\(x\) thay y = 5\(x\) vào \(x\) = 3y ta có: \(x\) = 3.5\(x\)
⇒ \(x\) = 15\(x\) ⇒ \(x-15x\) = 0 ⇒ \(-14\)\(x\) = 0 ⇒ \(x=0\)
Thay \(x\) = 0 vào y = 5\(x\) ta được: y= 5.0 = 0
Vậy \(x=3\)y; y = 5\(x\) thì y = 0

LB
Lê Bá Bảo nguyên
CTVHS
8 tháng 11
em chỉ thử làm thôi ạ:
Tương tự như thế vậy xuống 100m thì tăng 0,6 độ C và xuống 1000m thì tăng 6 độ C

27 tháng 10
Bài tập 3
tin tức và đã quyết định xin chào nộp đơn xin việc
Nhóm chúng tôi cần người giúp việc trẻ (18-25)
trại dành cho trẻ 10-14 tuổi. Nhiệm vụ bao gồm
hỗ trợ các trò chơi và các hoạt động khác,
Herpers phải nói được tiếng Anh hoặc tiếng Pháp và
có thể làm việc bất cứ lúc nào, kể cả một số
ings, từ ngày 5 đến ngày 25 tháng 7. Áp dụng một cách dí dỏm cho Ben Carroll
Trong khi 120-150 wont khi nộp đơn xin việc.

LN
Lưu Nguyễn Hà An
CTVHS
20 tháng 10
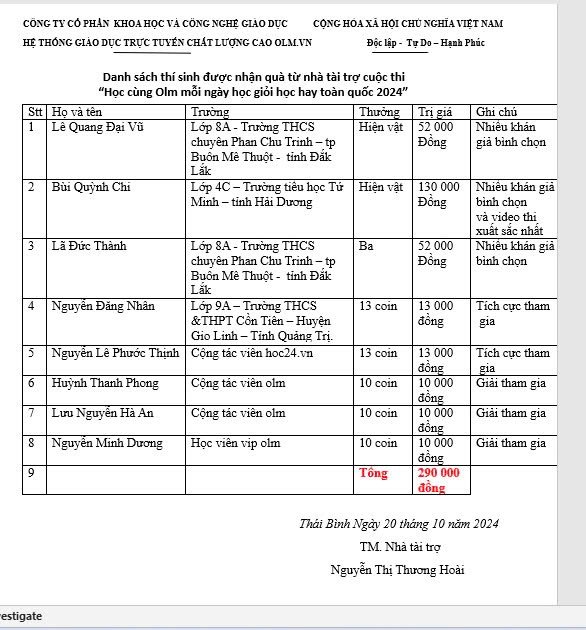
Em đăng ký nhận quà nhà tài trợ cuộc thi học cùng Olm mỗi ngày học giỏi học hay
LN
Lưu Nguyễn Hà An
CTVHS
20 tháng 10
Em đăng ký nhận coin từ nhà tài trợ cuộc thi học cùng Olm mỗi ngày học giỏi học hay.

NT
Nguyễn Tuấn Tú
CTVHS
7 tháng 10
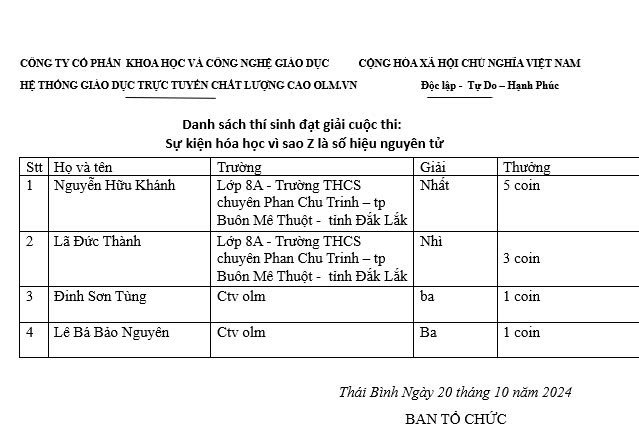
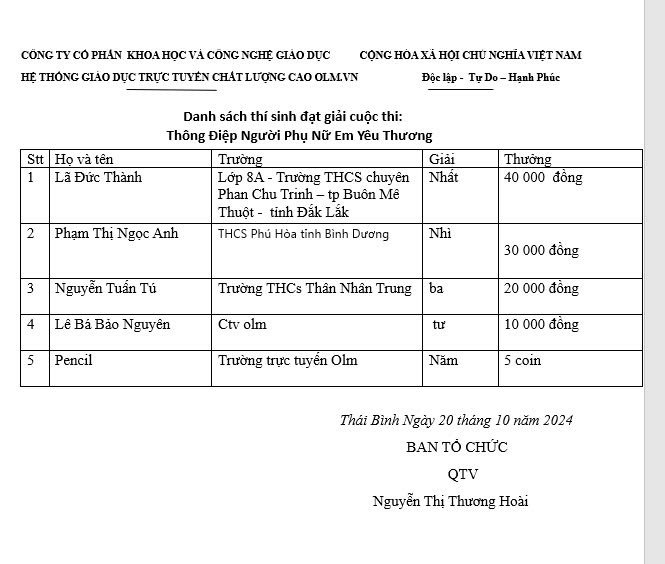
Em đăng ký nhận thưởng sự kiện: "Viết quan điểm của em về bạo lực học đường"

Ta có \(\sqrt{2+2\cos2x}=\sqrt{2+2\left(2\cos^2x-1\right)}=\sqrt{4\cos^2x}=2\left|\cos x\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|,\forall x\inℝ\) (1)
Đặt \(g\left(x\right)=f\left(x\right)-\left|\cos x\right|\)
Khi đó (1) \(\Leftrightarrow\left[f\left(x\right)-\left|\cos x\right|\right]+\left[f\left(-x\right)-\left|\cos x\right|\right]=0\)
\(\Leftrightarrow g\left(x\right)+\left[f\left(-x\right)-\left|\cos\left(-x\right)\right|\right]=0\) (do \(\cos x\) là hàm chẵn)
\(\Leftrightarrow g\left(x\right)+g\left(-x\right)=0\)
\(\Leftrightarrow g\left(x\right)=-g\left(-x\right)\)
\(\Leftrightarrow g\left(x\right)\) là hàm lẻ
Khi đó \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ. Thử lại, ta thấy:
(1) \(\Leftrightarrow f\left(x\right)+f\left(-x\right)=g\left(x\right)+\left|\cos x\right|+g\left(-x\right)+\left|\cos\left(-x\right)\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|\), thỏa mãn
Vậy \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ bất kì có tập xác định là \(ℝ\)
\(\Rightarrow I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}f\left(x\right)dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left[g\left(x\right)+\left|\cos x\right|\right]dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}g\left(x\right)dx+\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\) (do \(g\left(x\right)\) là hàm lẻ)
\(I=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-\cos x\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\cos xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-\cos x\right)dx\)
\(I=-\sin x|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+\sin x|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-\sin x|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\)
\(I=6\)