Ôn tập chương II SVIP

Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M, N.

Tứ giác DMCN là hình gì?

Chọn phương án trả lời chính xác nhất:

Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M, N.

Các điểm O, P, Q lần lượt là trung điểm của AB, AC, BC.

Chọn tên đoạn thẳng thích hợp:

+) DM.

+) MN $\perp$

+) MN $\perp$

+) MN là tiếp tuyến chung của

Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài tại DE, D ϵ (O), E ϵ (O'). Kẻ tiếp tuyến chung trong tại A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O'I và AE.

a) Tứ giác AMIN là

b) IM.

c) OO' là tiếp tuyến của đường tròn đường kính

Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB.

a) (O) và (O')

b) Kẻ dây DE của (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là

Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB. Kẻ dây DE của (O) vuông góc với AC tại trung điểm H của AC. Gọi K là giao điểm của BD và (O'). Chứng minh E, C, K thẳng hàng.

Sắp xếp các dòng sau theo thứ tự hợp lý:

Bài giải:

• ⇒ E, C, K thẳng hàng.
• Mặt khác, CE // AD (các cạnh đối của hình thoi).
• Do đó, qua C dó CK // AD và CE // AD nên các đường thẳng CK và CE trùng nhau.
• Dễ thấy tam giác ADB và tam giác CKB vuông nên AD $\perp$ DB và CK $\perp$ DB ⇒ AD // CK.

Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB. Kẻ dây DE của (O) vuông góc với AC tại trung điểm H của AC. Gọi K là giao điểm của BD và (O'). Chứng minh KH là tiếp tuyến của (O').

Sắp xếp các dòng sau theo thứ tự hợp lý:

Bài giải:

• Từ (1) và (2) suy ra: $\widehat{\text{HKC}}+\widehat{\text{O'KC}}=\widehat{\text{HEC}}+\widehat{\text{ECH}}=90^o$.
• Do đó HK là tiếp tuyến của (O').
• Tam giác vuông DKE có trung tuyến KH nên DH = KH = HE ⇒ $\widehat{\text{HKC}}=\widehat{\text{HEC}}$ (1)
• Suy ra $\widehat{\text{HKO'}}=\widehat{\text{HKC}}+\widehat{\text{O'KC}}=90^o$.
• Tam giác O'KC cân tại O' nên $\widehat{\text{O'KC}}=\widehat{\text{OCK}}=\widehat{\text{ECH}}$ (2)

Cho hai đường tròn (O ; R) và (O' ; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB và AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.

Tứ giác BDCE là

Cho hai đường tròn (O ; R) và (O' ; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB và AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC. Gọi là I giao điểm của EC và đường tròn (O'). Chứng minh D, A, I thẳng hàng.

Sắp xếp các dòng sau theo thứ tự hợp lý:

Bài giải:

• Ta thấy các tam giác ABD và tam giác AIC vuông nên AD $\perp$ BD và AI $\perp$ IC (hay AI $\perp$ EC).
• Các đường thẳng AD và AI cùng đi qua A và vuông góc với BD nên A, D, I thẳng hàng.
• Mặt khác, BD // EC (các cạnh đối của hình thoi), suy ra AI $\perp$ BD.

Cho hai đường tròn (O ; R) và (O' ; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB và AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC. Gọi là I giao điểm của EC và đường tròn (O'). Chứng minh KI là tiếp tuyến của (O').

Sắp xếp các dòng sau theo thứ tự hợp lý:

Bài giải:

• Do đó, $\widehat{\text{KIO'}}=\widehat{\text{KIA}}+\widehat{\text{O'IA}}=90^o.$ Suy ra KI là tiếp tuyến của đường tròn (O').
• Do đó, $\widehat{\text{KIA}}=\widehat{\text{KDA}}$. (1)
• Tam giác O'IA cân tại O' nên $\widehat{\text{O'IA}}=\widehat{\text{O'AI}}=\widehat{\text{DAK}}$. (2)
• Tam giác vuông DIE có IK là đường trung tuyến ứng với cạnh huyền nên IK = KD = KE.
• Từ (1) và (2) suy ra $\widehat{\text{KIA}}+\widehat{\text{O'IA}}=\widehat{\text{KDA}}+\widehat{\text{DAK}}=90^o$.

Hình vẽ

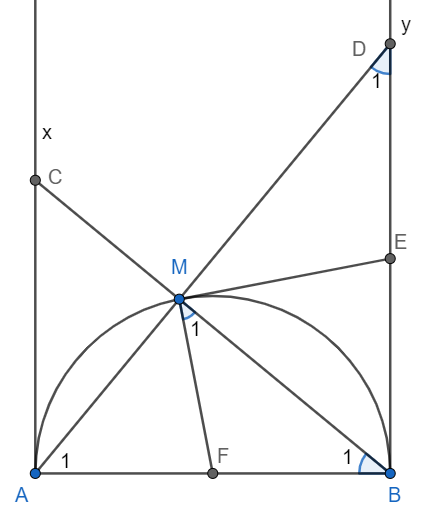
Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, vẽ các tia tiếp tuyến Ax và By với nửa đường tròn. Gọi M là điểm thuộc nửa đường tròn, D là giao điểm của AM và By, C là giao điểm của BM và Ax, E là trung điểm của BD. Chứng minh rằng ME là tiếp tuyến của nửa đường tròn.

Sắp xếp các dòng sau theo thứ tự hợp lý:

Bài giải:

• Vậy ME là tiếp tuyến của nửa đường tròn.
• Tam giác EBM cân nên $\widehat{M_2}=\widehat{B_2}$.
• Suy ra ME $\perp$ OM tại M.
• Suy ra $\widehat{M_1}+\widehat{M_2}=\widehat{B_1}+\widehat{B_2}=90^o$.