Bài học cùng chủ đề
- Đường thẳng song song với mặt phẳng
- Một số dạng toán về đường thẳng song song với mặt phẳng
- Đường thẳng song song với mặt phẳng
- Tìm thiết diện của mặt phẳng với khối chóp
- Bài tập mẫu: Chứng minh đường thẳng song song với mặt phẳng
- Bài tập mẫu: Dựng mặt phẳng song song với đường thẳng
- Bài tập mẫu: Thiết diện
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập mẫu: Dựng mặt phẳng song song với đường thẳng SVIP
Cho hình chóp S.ABC. Gọi M là trung điểm AC. Mặt phẳng $(\alpha)$ đi qua M và song song với SA;BC. Tìm thiết diện tạo bởi $(\alpha)$ và hình chóp, Thiết diện là hình gì?
Hướng dẫn giải:
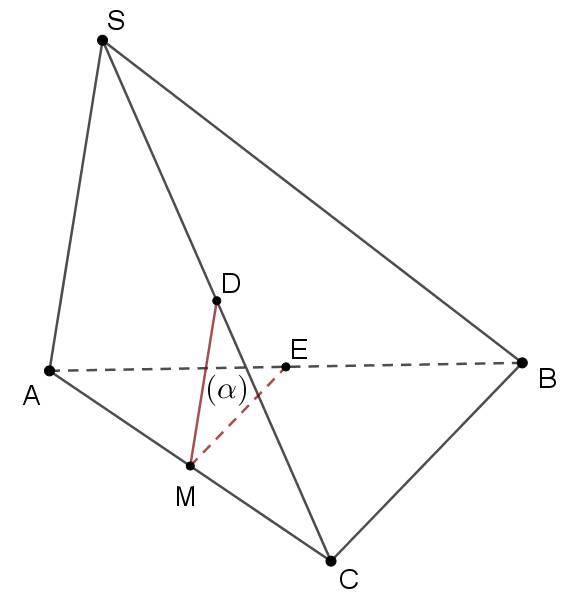
Trong (ABC): Kẻ ME song song với BC (E thuộc AB).
Trong (SAC): Kẻ MD song song với SA (D thuộc SC).
Vậy ($\alpha$) trùng với (MDE).
Trong (SBC): Kẻ DF song song với BC.
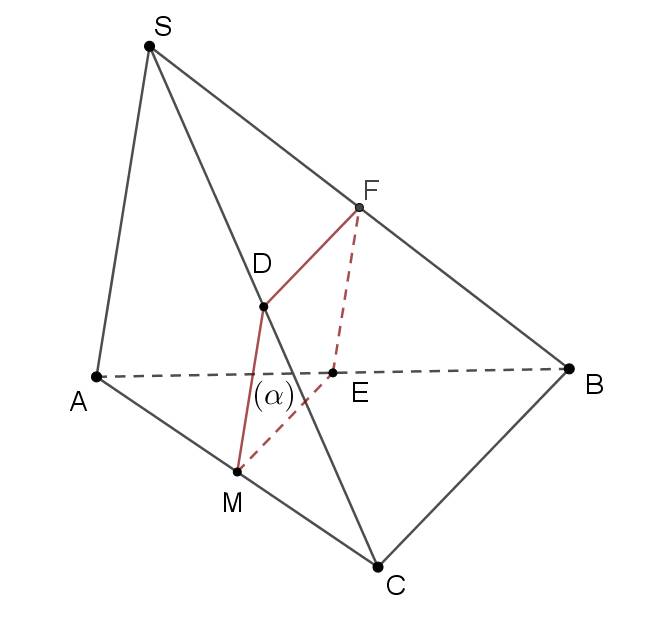
Vậy thiết diện cần tìm là hình thang MDFE (DF//BC//ME).
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên AB. Một mặt phẳng ($\alpha$) đi qua M và song song với SA và BC; ($\alpha$) cắt SB, SC, CD lần lượt tại N,P và Q.
a) Tứ giác MNPQ là hình gì?
b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định khi điểm M di động.
Hướng dẫn giải:
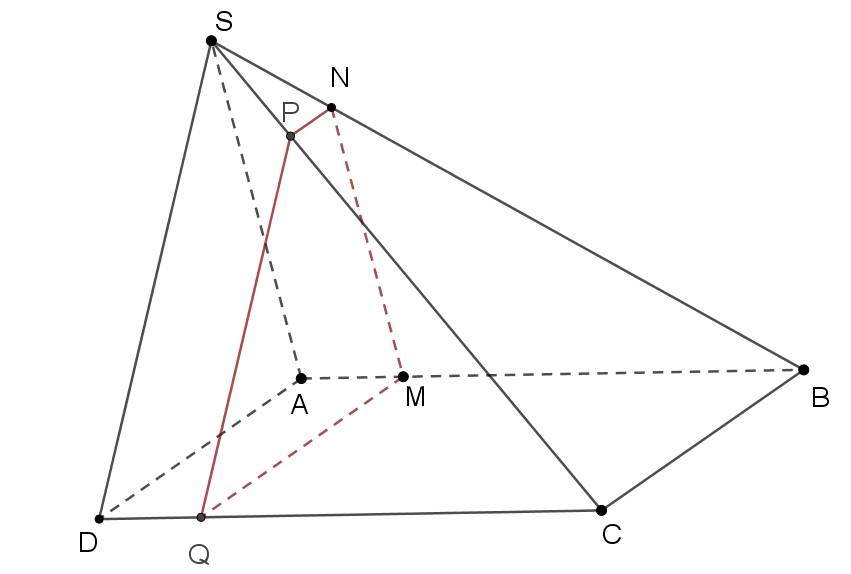
a) Trong (SAB): MN // SA (N $\in$ SB)
Trong (ABCD): MQ // BC (Q $\in$ DC).
Trong (SBC): NP // BC (P $\in$ SB).
Ta có MNPQ là hình thang do NP // MQ (// BC).
b) Nhận thấy khi M di động thì MN luôn nằm trong (SAB) và PQ luôn nằm trong (SDC), do đó giao điểm I của hai đường thẳng MN và PQ sẽ luôn nằm trên giao tuyến của (SAB) và (SDC).
