Bài tập tự luận: Chứng minh đẳng thức vectơ. Chứng minh ba điểm thẳng hàng SVIP

Hướng dẫn giải:

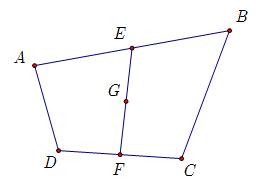
a) $\overrightarrow{A C}+\overrightarrow{B D}=\overrightarrow{A D}+\overrightarrow{B C}=2 \overrightarrow{E F}$

- $\overrightarrow{A C}+\overrightarrow{B D}=2 \overrightarrow{E F}(1)$.
Do $E$ là trung điểm $A B$ nên $2 \overrightarrow{O E}=\overrightarrow{O A}+\overrightarrow{O B}$ với $O$ là một điểm tùy ý.

Do $F$ là trung điểm $C D$ nên $2 \overrightarrow{O F}=\overrightarrow{O C}+\overrightarrow{O D}$ với $O$ là một điểm tùy ý.

(1) $\Leftrightarrow \overrightarrow{O C}-\overrightarrow{O A}+\overrightarrow{O D}-\overrightarrow{O B}=2 \overrightarrow{O F}-2 \overrightarrow{O E}$
$\begin{aligned}&\Leftrightarrow \overrightarrow{O C}-\overrightarrow{O A}+\overrightarrow{O D}-\overrightarrow{O B}=(\overrightarrow{O C}+\overrightarrow{O D})-(\overrightarrow{O A}+\overrightarrow{O B}) \\&\Leftrightarrow(\underbrace{\overrightarrow{O C}-\overrightarrow{O C}}_{\overrightarrow{0}})+(\underbrace{\overrightarrow{O D}-\overrightarrow{O D}}_{\overrightarrow{0}})-(\underbrace{\overrightarrow{O B}-\overrightarrow{O B}}_{\overrightarrow{0}})+(\underbrace{\overrightarrow{O A}-\overrightarrow{O A}}_{\overrightarrow{0}})=\overrightarrow{0} \Rightarrow \text { ĐPCM. }\end{aligned}$
$\overrightarrow{A D}+\overrightarrow{B C}=2 \overrightarrow{E F}(2)$

Do $E$ là trung điểm $A B$ nên $2 \overrightarrow{O E}=\overrightarrow{O A}+\overrightarrow{O B}$ với $O$ là một điểm tùy ý.

Do $F$ là trung điểm $C D$ nên $2 \overrightarrow{O F}=\overrightarrow{O C}+\overrightarrow{O D}$ với $O$ là một điểm tùy ý.

$(2) \Leftrightarrow \overrightarrow{O D}-\overrightarrow{O A}+\overrightarrow{O C}-\overrightarrow{O B}=2 \overrightarrow{O F}-2 \overrightarrow{O E}$
$\Leftrightarrow \overrightarrow{O D}-\overrightarrow{O A}+\overrightarrow{O C}-\overrightarrow{O B}=(\overrightarrow{O C}+\overrightarrow{O D})-(\overrightarrow{O A}+\overrightarrow{O B})$
$\Leftrightarrow(\underbrace{\overrightarrow{O C}-\overrightarrow{O C}}_{\overrightarrow{0}})+(\underbrace{\overrightarrow{O D}-\overrightarrow{O D}}_{\overrightarrow{0}})-(\underbrace{\overrightarrow{O B}-\overrightarrow{O B}}_{\overrightarrow{0}})+(\underbrace{\overrightarrow{O A}-\overrightarrow{O A}}_{\overrightarrow{0}})=\overrightarrow{0} \Rightarrow \text { ĐPCM. }$
b) $\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}+\overrightarrow{G D}=\overrightarrow{0}$ (3).

Do $E$ là trung điểm $A B$ nên $2 \overrightarrow{O E}=\overrightarrow{O A}+\overrightarrow{O B}$ với $O$ là một điểm tùy ý.

Do $F$ là trung điểm $C D$ nên $2 \overrightarrow{O F}=\overrightarrow{O C}+\overrightarrow{O D}$ với $O$ là một điểm tùy ý.

$(3) \Leftrightarrow(2 \overrightarrow{G E}-\overrightarrow{G B})+\overrightarrow{G B}+\overrightarrow{G C}+(2 \overrightarrow{G F}-\overrightarrow{G C})=\overrightarrow{0}$
$\Leftrightarrow 2 \overrightarrow{G E}+2 \overrightarrow{G F}=\overrightarrow{0} \Leftrightarrow 2(\underbrace{\overrightarrow{G E}+\overrightarrow{G F}}_{\overrightarrow{0}})=\overrightarrow{0} \Rightarrow \text { ĐPCM. }$

Hướng dẫn giải:

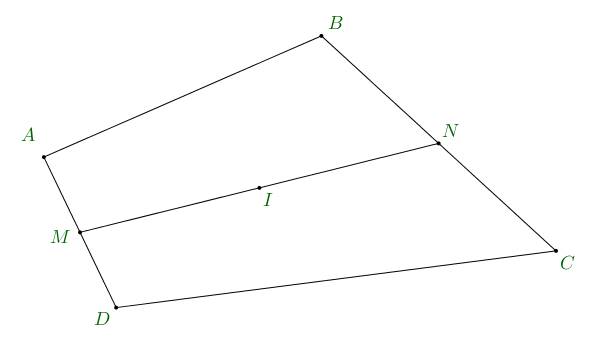
a) Chứng minh rằng $\overrightarrow{M N}=\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{D C})=\dfrac{1}{2}(\overrightarrow{A C}+\overrightarrow{D B})$.

- Chứng minh $\overrightarrow{M N}=\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{D C})$.

Vì $M$ là trung điểm của $A D$ nên $\overrightarrow{M A}+\overrightarrow{M D}=\overrightarrow{0}$.

Vì $N$ là trung điểm của $B C$ nên $\overrightarrow{B N}+\overrightarrow{C N}=\overrightarrow{0}$.
Áp dụng quy tắc ba điểm, ta có:

$\left\{\begin{array}{l}\overrightarrow{M N}=\overrightarrow{M A}+\overrightarrow{A B}+\overrightarrow{B N} \\ \overrightarrow{M N}=\overrightarrow{M D}+\overrightarrow{DC}+\overrightarrow{C N}\end{array}\right.$ $\Rightarrow 2 \overrightarrow{M N}=(\overrightarrow{M A}+\overrightarrow{M D})+\overrightarrow{A B}+\overrightarrow{C D}+(\overrightarrow{B N}+\overrightarrow{C N})=\overrightarrow{0}+\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{0}=\overrightarrow{A B}+\overrightarrow{C D} .$ $\Rightarrow \overrightarrow{M N}=\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{D C}) .$

- Chứng minh $\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{D C})=\dfrac{1}{2}(\overrightarrow{A C}+\overrightarrow{D B}) .$ $\{\overrightarrow{A B}=\overrightarrow{A C}+\overrightarrow{C B}=\overrightarrow{D B}=\overrightarrow{C D}+\overrightarrow{B C}=\overrightarrow{A C}+\overrightarrow{D B}+\overrightarrow{C B}+\overrightarrow{B C}=\overrightarrow{A C}+\overrightarrow{D B} \Rightarrow .$

Vậy: $\overrightarrow{M N}=\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{D C})=\dfrac{1}{2}(\overrightarrow{A C}+\overrightarrow{D B})$.

b) Gọi $I$ là trung điểm của $M N$. Chứng minh rằng: $\overrightarrow{I A}+\overrightarrow{I B}+\overrightarrow{I C}+\overrightarrow{I D}=\overrightarrow{0}$.

Áp dụng hệ thức trung điểm, ta có:

$\left\{\begin{array}{l}\overrightarrow{I A}+\overrightarrow{I D}=2 \overrightarrow{I M} \\\overrightarrow{I B}+\overrightarrow{I D}=2 \overrightarrow{I N}\end{array} \Rightarrow \overrightarrow{I A}+\overrightarrow{I D}+\overrightarrow{I B}+\overrightarrow{I D}=2(\overrightarrow{I M}+\overrightarrow{I N})=   2.\overrightarrow{0}=\overrightarrow{0} .\right.$

Hướng dẫn giải:

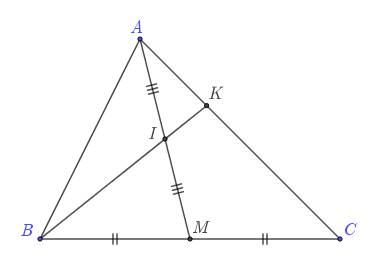
$=\dfrac{1}{2} \overrightarrow{B A}+\dfrac{1}{4} \overrightarrow{B C}=\dfrac{1}{2}(\overrightarrow{B K}+\overrightarrow{K A})+\dfrac{1}{4}(\overrightarrow{B K}+\overrightarrow{K C})=\dfrac{3}{4} \overrightarrow{B K}+\dfrac{1}{2} \overrightarrow{K A}+\dfrac{1}{4} \overrightarrow{K C}$
Mà $A K=\dfrac{1}{3} A C$ nên $K C=2 K A$ suy ra $\overrightarrow{K C}=-2 \overrightarrow{K A} \Leftrightarrow \overrightarrow{K C}+2 \overrightarrow{K A}=\overrightarrow{0} \Leftrightarrow \dfrac{1}{4} \overrightarrow{K C}+\dfrac{1}{2} \overrightarrow{K A}=\overrightarrow{0}.$
Do đó $\overrightarrow{B I}=\dfrac{3}{4} \overrightarrow{B K}+\overrightarrow{0}=\dfrac{3}{4} \overrightarrow{B K}$. Vậy ba điểm $B, I, K$ thẳng hàng.

Hướng dẫn giải:

Ta có $\overrightarrow{B C}+\overrightarrow{M A}=\overrightarrow{0} \Leftrightarrow \overrightarrow{M A}=-\overrightarrow{B C}$ nên $M A / / B C$.
Do đó $M \notin A C$ (1).
Ta có $\overrightarrow{A B}-\overrightarrow{N A}-3 \overrightarrow{A C}=\overrightarrow{0}$
$\Leftrightarrow \overrightarrow{A B}-(\overrightarrow{N M}+\overrightarrow{M A})-3 \overrightarrow{A C}=\overrightarrow{0}$
$\Leftrightarrow \overrightarrow{A B}-\overrightarrow{N M}-\overrightarrow{M A}-3 \overrightarrow{A C}=\overrightarrow{0}$
$\Leftrightarrow \overrightarrow{N M}=\overrightarrow{A B}-\overrightarrow{M A}-3 \overrightarrow{A C}$
$\Leftrightarrow \overrightarrow{N M}=\overrightarrow{A B}+\overrightarrow{B C}-3 \overrightarrow{A C}=\overrightarrow{A C}-3 \overrightarrow{A C}=-2 \overrightarrow{A C}$ (2).
Từ $(1),(2)$ ta có $M N / / A C$.

Hướng dẫn giải:

a) Tính $\overrightarrow{I J} ; \overrightarrow{I K}$ theo $\overrightarrow{A B} ; \overrightarrow{A C}$.
Ta có: $\overrightarrow{I J}=\overrightarrow{I C}+\overrightarrow{C J}=-\overrightarrow{B C}-\dfrac{1}{3} \overrightarrow{A C}=-(\overrightarrow{B A}+\overrightarrow{A C})-\dfrac{1}{3} \overrightarrow{A C}=\overrightarrow{A B}-\dfrac{4}{3} \overrightarrow{A C}$.
$\overrightarrow{I K}=\overrightarrow{I B}+\overrightarrow{B K}=-2 \overrightarrow{B C}-\dfrac{1}{2} \overrightarrow{A B}=-2(\overrightarrow{B A}+\overrightarrow{A C})-\dfrac{1}{2} \overrightarrow{A B}=\dfrac{3}{2} \overrightarrow{A B}-2 \overrightarrow{A C} .$
b) Chứng minh ba điểm $I, J, K$ thẳng hàng.
Theo câu a: $\left\{\begin{array}{l}\overrightarrow{I J}=\overrightarrow{A B}-\dfrac{4}{3} \overrightarrow{A C} \\ \overrightarrow{I K}=\dfrac{3}{2} \overrightarrow{A B}-2 \overrightarrow{A C}\end{array} \Leftrightarrow\left\{\begin{array}{l}\overrightarrow{I J}=\overrightarrow{A B}-\dfrac{4}{3} \overrightarrow{A C} \\ \overrightarrow{I K}=\dfrac{3}{2}\left(\overrightarrow{A B}-\dfrac{2}{4} \overrightarrow{A C}\right)\end{array} \Rightarrow \overrightarrow{I K}=\dfrac{3}{2} \overrightarrow{I J} .\right.\right.$ $\Rightarrow I, J, K$ thẳng hàng.

Hướng dẫn giải:

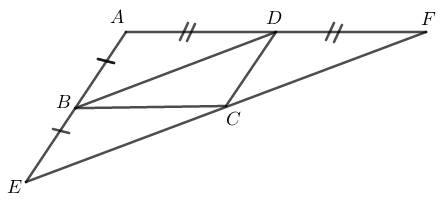
a) Ba điểm $F, C, E$ thẳng hàng.
Theo đề ra ta có $D$ là trung điểm của đoạn thẳng $A F, B$ là trung điểm của đoạn thẳng $A E$.
Ta có $\overrightarrow{C E}=\overrightarrow{C B}+\overrightarrow{B E}=\overrightarrow{D A}+\overrightarrow{A B}=\overrightarrow{F D}+\overrightarrow{D C}=\overrightarrow{F C}$ nên ba điểm $F, C, E$ thẳng hàng..
b) Các tứ giác $B D C E, B D F C$ là hình bình hành.
Ta có $\left\{\begin{array}{l}B E / / D C \\ B E=D C\end{array} \Rightarrow B D C E\right.$ là hình bình hành.
Ta có $\left\{\begin{array}{l}D F / / B C \\ D F=B C\end{array} \Rightarrow B D F C\right.$ là hình bình hành.

Hướng dẫn giải:

Ta có $\left\{\begin{array}{l}\overrightarrow{I A}+3 \overrightarrow{I C}=\overrightarrow{0} \\ \overrightarrow{J A}+2 \overrightarrow{J B}+3 \overrightarrow{J C}=\overrightarrow{0}\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}\overrightarrow{I A}+3 \overrightarrow{I C}=\overrightarrow{0} \\ (\overrightarrow{J I}+\overrightarrow{I A})+2(\overrightarrow{J I}+\overrightarrow{I B})+3(\overrightarrow{J I}+\overrightarrow{I C})=\overrightarrow{0}\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}\overrightarrow{I A}+3 \overrightarrow{I C}=\overrightarrow{0} \\ 6 \overrightarrow{J I}+2 \overrightarrow{I B}+(\overrightarrow{I A}+3 \overrightarrow{I C})=\overrightarrow{0}\end{array}\right.$
$\Rightarrow 6 \overrightarrow{J I}+2 \overrightarrow{I B}=\overrightarrow{0} \Leftrightarrow \overrightarrow{I B}=-3 \overrightarrow{J I} .$
Vậy ba điểm $I, J, B$ thẳng hàng.

Hướng dẫn giải:

Gọi $G, G^{\prime}$ lần lượt là trọng tâm của các $\triangle A B C$ và $\triangle A^{\prime} B^{\prime} C^{\prime}$.
Khi đó $\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}=\overrightarrow{0}$ và $\overrightarrow{G^{\prime} A^{\prime}}+\overrightarrow{G^{\prime} B^{\prime}}+\overrightarrow{G^{\prime} C^{\prime}}=\overrightarrow{0}$.
Ta đạ̄t: $\dfrac{A A^{\prime}}{A B}=\dfrac{B B^{\prime}}{B C}=\dfrac{C C^{\prime}}{A C}=k>0 \Rightarrow\left\{\begin{array}{l}\overrightarrow{A A^{\prime}}=k \overrightarrow{A B} \\ \overrightarrow{B B^{\prime}}=k \overrightarrow{B C} . \\ \overrightarrow{C C^{\prime}}=k \overrightarrow{C A}\end{array}\right.$
Do $G$ là trọng tâm của các $\triangle A B C$ nên $\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}=\overrightarrow{0}$
$\begin{aligned}&\Leftrightarrow\left(\overrightarrow{G G^{\prime}}+\overrightarrow{G^{\prime} A^{\prime}}+\overrightarrow{A^{\prime} A}\right)+\left(\overrightarrow{G G^{\prime}}+\overrightarrow{G^{\prime} B^{\prime}}+\overrightarrow{B^{\prime} B}\right)+\left(\overrightarrow{G G^{\prime}}+\overrightarrow{G^{\prime} C^{\prime}}+\overrightarrow{C^{\prime} C}\right)=\overrightarrow{0} \\ &\Leftrightarrow 3 \overrightarrow{G G^{\prime}}+\left(\overrightarrow{G^{\prime}A^{\prime}}+\overrightarrow{G^{\prime}B^{\prime}}+\overrightarrow{G^{\prime} C^{\prime}}\right)-\left(\overrightarrow{A A^{\prime}}+\overrightarrow{B B^{\prime}}+\overrightarrow{C C^{\prime}}\right)=\overrightarrow{0} \\ &\Leftrightarrow 3 \overrightarrow{G G^{\prime}}+\quad-k(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A})=\overrightarrow{0} \\ &\Leftrightarrow 3 \overrightarrow{G G^{\prime}}-k \cdot \overrightarrow{0}=\overrightarrow{0} \\ &\Leftrightarrow 3 \overrightarrow{G G^{\prime}}=\overrightarrow{0} \Leftrightarrow G \equiv G^{\prime} \end{aligned}$

Hướng dẫn giải:

a) Chứng minh ba đường thẳng $A A^{\prime}, B B^{\prime}, C C^{\prime}$ đồng quy tại một điểm $N$.
a) Gọi $O, P, Q$ lần lượt là trung điểm của các cạnh $A A^{\prime}, B B^{\prime}, C C^{\prime}$. Ta có:
$\begin{aligned} &\overrightarrow{M O}=\dfrac{1}{2}\left(\overrightarrow{M A}+\overrightarrow{M A^{\prime}}\right)=\dfrac{1}{2}(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}) \\ &\overrightarrow{M P}=\dfrac{1}{2}\left(\overrightarrow{M B}+\overrightarrow{M B^{\prime}}\right)=\dfrac{1}{2}(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}) \\ &\overrightarrow{M Q}=\dfrac{1}{2}\left(\overrightarrow{M A}+\overrightarrow{M C^{\prime}}\right)=\dfrac{1}{2}(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}) \\ &\Rightarrow \overrightarrow{M O}=\overrightarrow{M P}=\overrightarrow{M Q} \Rightarrow O \equiv P \equiv Q . \end{aligned}$
Do đó ba đường thẳng $A A^{\prime}, B B^{\prime}, C C^{\prime}$ đồng quy tại trung điểm $N(\equiv O \equiv P \equiv Q)$ của mỗi đường.
b)

Chứng minh rằng khi $M$ di động đường thẳng $M N$ luôn đi qua trọng tâm $G$ của $\triangle A B C$.
Vì $G$ là trọng tâm của $\triangle A B C$ nên ta có $\overrightarrow{M G}=\dfrac{1}{3}(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C})$.
Mặt khác $\overrightarrow{M N}=\dfrac{1}{2}(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C})$.
Suy ra $\overrightarrow{M G}=\dfrac{2}{3} \overrightarrow{M N}$. Do đó 3 điểm $M, N, G$ thẳng hàng.
Vậy khi $M$ di động đường thẳng $M N$ luôn đi qua trọng tâm $G$ của $\triangle A B C$.

Hướng dẫn giải:

Vì $G_{1}$ là trọng tâm tam giác $B C A_{1}$ nên $3 \overrightarrow{G G_{1}}=\overrightarrow{G B}+\overrightarrow{G C}+\overrightarrow{G A}_{1}$
Tương tự $G_{2}, G_{3}$ lần lượt là trọng tâm tam giác $A B C_{1}, A C B_{1}$ suy ra $3 \overrightarrow{G G_{2}}=\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C_{1}}$ và $3 \overrightarrow{G G_{3}}=\overrightarrow{G A}+\overrightarrow{G C}+\overrightarrow{G B_{1}}$
Công theo vế với vế các đẳng thức trên ta có
$$
\overrightarrow{G G_{1}}+\overrightarrow{G G_{2}}+\overrightarrow{G G_{3}}=2(\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C})+\left(\overrightarrow{G A_{1}}+\overrightarrow{G B_{1}}+\overrightarrow{G C_{1}}\right)
$$
Mặt khác hai tam giác $A B C$ và $A_{1} B_{1} C_{1}$ có cùng trọng tâm $\mathrm{G}$ nên
$$
\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}=\overrightarrow{0} \text { và } \overrightarrow{G A_{1}}+\overrightarrow{G B_{1}}+\overrightarrow{G C_{1}}
$$
Suy ra $\overrightarrow{G G_{1}}+\overrightarrow{G G_{2}}+\overrightarrow{G G_{3}}=\overrightarrow{0}$

Hướng dẫn giải:

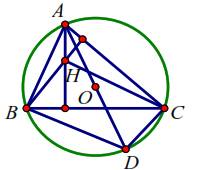
Cho tam giác $A B C$ có trực tâm $\mathrm{H}$, trọng tâm $\mathrm{G}$ và tâm đường tròn ngoại tiếp $\mathrm{O}$. Chứng minh rằng
a) $\overrightarrow{H A}+\overrightarrow{H B}+\overrightarrow{H C}=2 \overrightarrow{H O}$
b) $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O H}$
c) $\overrightarrow{G H}+2 \overrightarrow{G O}=\overrightarrow{0}$
a) Dễ thấy $\overrightarrow{H A}+\overrightarrow{H B}+\overrightarrow{H C}=2 \overrightarrow{H O}$ nếu tam giác $A B C$
vuông thấy $\overrightarrow{H A}+\overrightarrow{H B}+\overrightarrow{H C}=2 \overrightarrow{H O}$ nếu tam giác $A B C$ vuông
Nếu tam giác $A B C$ không vuông gọi $\mathrm{D}$ là điểm đối xứng của A qua $\mathrm{O}$ khi đó
$B H / / D C$ (vì cùng vuông góc với $\mathrm{AC}$ )
$B D / / C H$ (vì cùng vuông góc với $\mathrm{AB}$ )
Suy ra $B D C H$ là hình bình hành, do đó theo quy tắc hình bình hành thì $\overrightarrow{H B}+\overrightarrow{H C}=\overrightarrow{H D}$ (1)

Mặt khác vì $\mathrm{O}$ là trung điểm của $\mathrm{AD}$ nên $\overrightarrow{H A}+\overrightarrow{H D}=2 \overrightarrow{H O}$
Hinh $1.17$
(2)
Từ (1) và (2) suy ra $\overrightarrow{H A}+\overrightarrow{H B}+\overrightarrow{H C}=2 \overrightarrow{H O}$
b) Theo câu a) ta có
$ \begin{aligned} &\overrightarrow{H A}+\overrightarrow{H B}+\overrightarrow{H C}=2 \overrightarrow{H O} \\ &\Leftrightarrow(\overrightarrow{H O}+\overrightarrow{O A})+(\overrightarrow{H O}+\overrightarrow{O B})+(\overrightarrow{H O}+\overrightarrow{O C})=2 \overrightarrow{H O} \\ &\Leftrightarrow \overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O H} \text { đpcm } \end{aligned} $
c) Vì G là trọng tâm tam giác $A B C$ nên $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=3 \overrightarrow{O G}$
Mặt khác theo câu b) ta có $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O H}$
Suy ra $\overrightarrow{O H}=3 \overrightarrow{O G} \Leftrightarrow(\overrightarrow{O G}+\overrightarrow{G H})-3 \overrightarrow{O G}=\overrightarrow{0} \Leftrightarrow \overrightarrow{G H}+2 \overrightarrow{G O}=\overrightarrow{0}$

Hướng dẫn giải:

Cách 1:

Gọi D là chân đường phân giác góc $\mathrm{A}$
Do D là đường phân giác giác trong góc $\mathrm{A}$ nên ta có
$\begin{aligned} &\dfrac{D B}{D C}=\dfrac{c}{b} \Rightarrow \overrightarrow{B D}=\dfrac{c}{b} \overrightarrow{D C} \\ &\Leftrightarrow \overrightarrow{I D}-\overrightarrow{I B}=\dfrac{c}{b}(\overrightarrow{I C}-\overrightarrow{I D}) \\ &\Leftrightarrow(b+c) \overrightarrow{I D}=b \overrightarrow{I B}+c \overrightarrow{I C}(1) \end{aligned}$
Do I là chân đường phân giác nên ta có :
$\begin{aligned} &\dfrac{I D}{I A}=\dfrac{B D}{B A}=\dfrac{C D}{C A}=\dfrac{B D+C D}{B A+C A}=\dfrac{a}{b+c} \\ &\Rightarrow(b+c) \overrightarrow{I D}=-a \overrightarrow{I A}(2) \end{aligned}$
Từ (1) và (2) ta có điều phải chứng minh
Cách 2:

Qua $\mathrm{C}$ dựng đường thẳng song song với $\mathrm{AI}$ cắt $\mathrm{BI}$ tai $\mathrm{B}^{\prime}$;song song với $\mathrm{BI}$ cắt $\mathrm{AI}$ tại A'
Ta có $\overrightarrow{I C}=\overrightarrow{I A^{\prime}}+\overrightarrow{I B^{\prime}}$ (*)
Theo định lý Talet và tính chất đường phân giác trong ta có :
$ \dfrac{I B}{I B^{\prime}}=\dfrac{B A_{1}}{C A_{1}}=\dfrac{c}{b} \Rightarrow \overrightarrow{I B^{\prime}}=-\dfrac{b}{c} \overrightarrow{I B} \text { (1) } $
Tương tự : $\overrightarrow{I A^{\prime}}=-\dfrac{a}{c} \overrightarrow{I A}$ (2)
Từ (1) và (2) thay vào (*) ta có :
$\overrightarrow{I C}=-\dfrac{a}{c} \overrightarrow{I A}-\dfrac{b}{c} \overrightarrow{I B} \Leftrightarrow a \overrightarrow{I A}+b \overrightarrow{I B}+c \overrightarrow{I C}=\overrightarrow{0} $.