Bài toán thực tế ứng dụng tỉ số lượng giác của góc nhọn SVIP

Dùng máy tính cầm tay, tính $\sin 40^\circ 12'$ (làm tròn đến chữ số thập phân thứ ba).

Trả lời:

Dùng máy tính cầm tay, tính $\tan 63^\circ 36'$ (làm tròn đến chữ số thập phân thứ hai).

Trả lời:

Dùng máy tính cầm tay, tính góc $\alpha$ biết $\tan \alpha = 0,78$ (làm tròn đến độ).

Trả lời: $^\circ$

Hình sau mô tả tia nắng mặt trời dọc theo $AB$ tạo với phương nằm ngang trên mặt đất một góc $\alpha = \widehat{ABH}$. Sử dụng máy tính cầm tay, tính số đo góc $\alpha$ (làm tròn kết quả đến hàng đơn vị của độ) biết $AH = 2$ m, $BH = 5$ m.

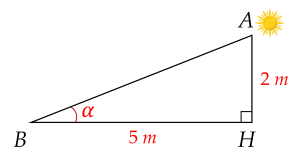
Trả lời: $^\circ$

Tia nắng chiếu qua nóc của một tòa nhà hợp với mặt đất một góc $\alpha$. Cho biết tòa nhà cao $21$ m và bóng của nó trên mặt đất dài $15$ m.

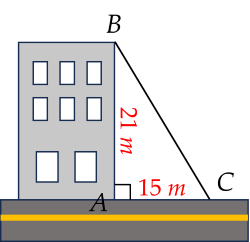
Tính góc $\alpha$ (kết quả làm tròn đến độ).

Trả lời: $^\circ$

Một cái thang $12$ m được đặt vào một bức tường sao cho chân thang cách tường $7$ m (như hình vẽ).

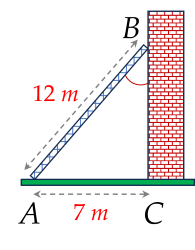
Tính góc tạo bởi thang và tường (làm tròn đến phút).

Trả lời: $^\circ$  phút.

Một máy bay đang bay ở độ cao $12$ km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất. Nếu cách sân bay $320$ km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?

Trả lời: $^\circ$ $^\prime$

Để ước lượng chiều cao của một tháp mà không cần lên đỉnh tháp, người ta sử dụng giác kế, thước cuộn, máy tính cầm tay. Ở hình bên, để đo chiều cao $AD$ của tháp, người ta đặt giác kế tại một điểm quan sát cách chân tháp một khoảng $CD = OB = a$, trong đó chiều cao của điểm đặt giác kế là $OC = b$. Quay thanh giác kế sao cho khi ngắm thanh này ta nhìn thấy đỉnh $A$ của tháp, đọc trên giác kế số đo $\alpha$ của góc $AOB$.

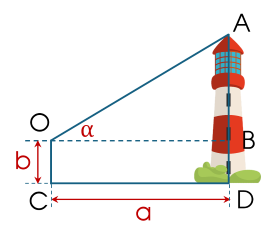
Tính chiều cao của tháp, biết $\alpha = 42^\circ$, $b = 13,81$ m; $a = 90$ m (làm tròn đến hàng phần mười của mét).

Trả lời:  m.