Các góc ở vị trí đặc biệt SVIP

I. HAI GÓC KỀ BÙ

Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.

Hai góc bù nhau là hai góc có tổng số đo bằng $180\degree$.

Hai góc vừa kề nhau, vừa bù nhau được gọi là hai góc kề bù.

Ví dụ: 

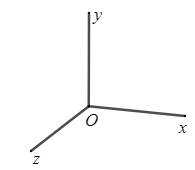
Hình 1

Trong Hình 1, \(\widehat{xOy}\) và \(\widehat{yOz}\) là hai góc kề nhau với cạnh chung là $Oy$, \(\widehat{yOz}\) và \(\widehat{zOx}\) là hai góc kề nhau với cạnh chung là $Oz$, \(\widehat{xOz}\) và \(\widehat{xOy}\) là hai góc kề nhau với cạnh chung là $Ox$.

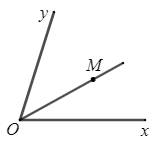
Chú ý: Nếu $M$ là điểm trong của góc $xOy$ thì \(\widehat{xOM}+\widehat{MOy}=\widehat{xOy}\).

2. HAI GÓC ĐỐI ĐỈNH

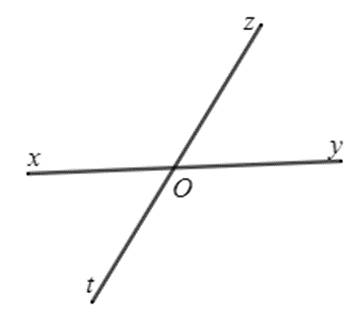
Hình 2

Cho hai đường thẳng $xy$ và $zt$ cắt nhau tại $O$ (Hình 2). Ta gọi $Oy$ là tia đối của tia $Ox$ và gọi tia $Ot$ là tia đối của tia $Oz$.

Ta thấy \(\widehat{xOt}\) và \(\widehat{yOz}\) có chung đỉnh $O$. 

\(\widehat{xOt}\) và \(\widehat{yOz}\) được gọi là hai góc đối đỉnh.

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Chú ý: Khi \(\widehat{xOt}\) và \(\widehat{yOz}\) là hai góc đối đỉnh, ta còn nói: \(\widehat{xOt}\) đối đỉnh với \(\widehat{yOz}\); \(\widehat{yOz}\) đối đỉnh với \(\widehat{xOt}\); \(\widehat{xOt}\) và \(\widehat{yOz}\) đối đỉnh với nhau.

3. TÍNH CHẤT CỦA HAI GÓC ĐỐI ĐỈNH

Ta có tính chất:

Hai góc đối đỉnh thì bằng nhau.

Ví dụ: 

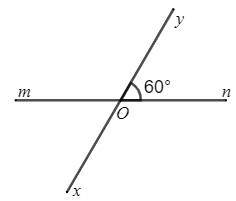
Hình 3

Trong Hình 3 ta có \(\widehat{nOy}\) và \(\widehat{mOx}\) là hai góc đối đỉnh nên \(\widehat{nOy}=\widehat{mOx}=60^0\).

Chú ý: Hai đường thẳng vuông góc

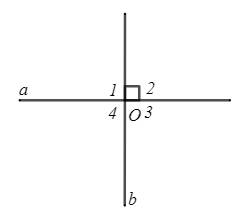
Hai đường thẳng $a$ và $b$ cắt nhau tịa $O$ tạo thành bốn góc $\hat O_1$, $\hat O_2$, $\hat O_3$, $\hat O_4$. Do tính chất của hai góc đối đỉnh hoặc kề bù, ta nhận thấy trong số bốn góc nêu trên, nếu có một góc vuông thì ba góc còn lại cũng là góc vuông. Khi đó ta nói hai đường thẳng $a$ và $b$ vuông góc với nhau và kí hiệu là \(a\perp b\) hoặc \(b\perp a\).