Đề kiểm tra chương IV: Góc và đường thẳng song song SVIP

Hướng dẫn giải:

+ Hai cặp góc so le trong: góc B₁ và góc A₃; góc A₄ và góc B₂ .

+ Bốn cặp góc đồng vị: góc B₁ và góc A₁; góc B₂ và góc A₂; góc B₃ và góc A₃; góc B₄ và góc A₄ .

Hướng dẫn giải:

a) Ta có: $\left\{\begin{aligned} & \widehat{A_{4}}=110^{\circ} \\ & \widehat{B_{2}}=110^{\circ} \\ \end{aligned}\right.  \Rightarrow \widehat{A_{4}}=\widehat{B_{2}}=110^{\circ}$.

Mà hai góc ờ vị trí so le trong $\Rightarrow $ $a // b$.

b) Ta có: $\left\{ \begin{aligned} & c \perp a \\ & a // b \\ \end{aligned}\right. \Rightarrow c \perp b$

c) Vì $a  // b \Rightarrow \widehat{A_{4}}+\widehat{B_{1}}=180^{\circ}$

Mà hai góc ở vị trí trong cùng phía $\Rightarrow \widehat{B_{1}}=180^{\circ}-\widehat{A_{4}}=70^{\circ}$.

Vì $b \perp c$; $e \perp c$ và $b // e$

$\Rightarrow \widehat{B_{2}}=\widehat{C_{2}}=110^{\circ}$ (hai góc ở vị trí đồng vị)

Ta có $\widehat{C_{2}}$ và $\widehat{C_{3}}$ là hai góc kề bù $\Rightarrow \widehat{C_{2}}+\widehat{C_{3}}=180^{\circ}$

$\Rightarrow \widehat{C_{3}}=180^{\circ}-\widehat{C_{2}}=70^{\circ}$.

Hướng dẫn giải:

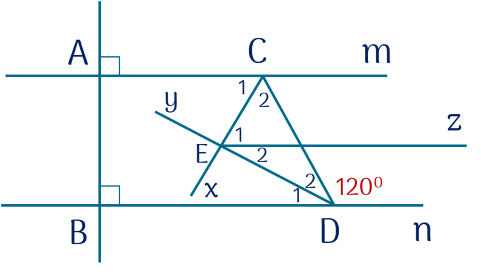
Kẻ tia $Cx$ là tia phân giác của $\widehat{A C D}$ và $Dy$ là tia phân giác của $\widehat{B D C}$, hai tia $Cx$ và $Dy$ cắt nhau tại $E$.

$\widehat{C_1}=\widehat{C_2}=60^{\circ}$ và $\widehat{D_1}=\widehat{D_2}=30^{\circ}$

Kẻ tia $Ez / / m // n$, tính $\widehat{E_1}=60^{\circ}$ và $\widehat{E_2}=30^{\circ}$

Suy ra $\widehat{CED}=90^{\circ}$.