Đề kiểm tra giữa học kì I toán 12 cấu trúc mới mới nhất

Câu 1 (1đ):

Cho hàm số $y=-x^3-3x^2+9x-1$ . Mệnh đề nào sau đây đúng?

Hàm số đồng biến trên khoảng

(-3;\,1).

Hàm số đồng biến trên khoảng

(-\infty;\,-3).

Hàm số đồng biến trên khoảng

(1;\,+\infty).

Hàm số nghịch biến trên khoảng

(-3;\,+\infty).

Câu 2 (1đ):

Cho hàm số $y=f\left(x \right)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của ${f}'\left(x \right)$ như sau:

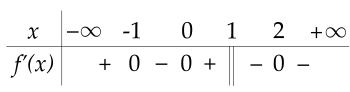
loading...

Số điểm cực đại của hàm số đã cho là

2

.

3

.

1

.

4

.

Câu 3 (1đ):

Cho hàm số $y=f(x)$ có đồ thị là đường cong như hình vẽ:

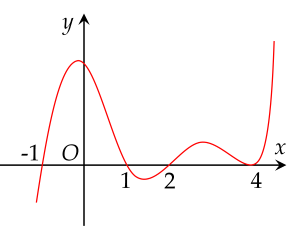
loading...

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

(-\infty ;\,-1)

.

(0;\,1)

.

(1;\,2)

.

(-1;\,1).

Câu 4 (1đ):

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=x+\dfrac{1}{x}$ trên đoạn $\Big[ \dfrac{3}{2};\,3 \Big]$ lần lượt là

\dfrac{16}{3}

,

2

.

\dfrac{10}{3}

,

\dfrac{13}{6}

.

\dfrac{10}{3}

,

2

.

\dfrac{10}{3}

,

\dfrac{5}{2}

.

Câu 5 (1đ):

Cho hàm số $y=f(x )$ có $\underset{x\to +\infty }{\mathop{\lim }}\,f(x )=2$ , $\underset{x\to -\infty }{\mathop{\lim }}\,f(x )=+\infty$ . Khẳng định nào sau đây đúng?

A

Đồ thị hàm số đã cho có một tiệm cận ngang.

B

Đồ thị hàm số đã cho không có tiệm cận ngang

C

Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng

x=2

.

D

Đồ thị hàm số đã cho có hai tiệm cận ngang phân biệt.

Câu 6 (1đ):

Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?

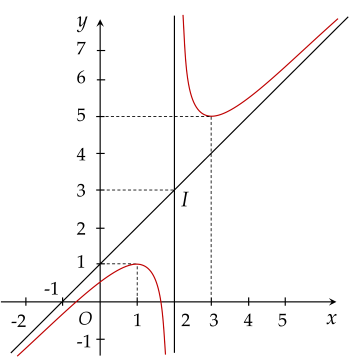
loading...

y=\dfrac{x^{2}-2 x-1}{x-2}

.

y=\dfrac{x^{2}-x-1}{x+2}

.

y=\dfrac{x^{2}-x+1}{x-2}

.

y=\dfrac{x^{2}-x-1}{x-2}

.

Câu 7 (1đ):

Câu 8 (1đ):

Câu 9 (1đ):

Điểm nào sau đây thuộc đồ thị của hàm số $y=x^4-3x^2-5$ ?

Điểm

P(1;3)

.

Điểm

M(-1;-3)

.

Điểm

N(2;-1)

.

Điểm

Q(-2;-9)

.

Câu 10 (1đ):

Định luật vạn vật hấp dẫn của Newton được cho bởi công thức $F=G\dfrac{m_1.m_2}{r^2}$ . Trong đó $F$ là lực hấp dẫn giữa hai vật thể bất kì, $G$ là hằng số hấp dẫn, $m_1,\,m_2$ là khối lượng các vật, $r$ là khoảng cách giữa chúng. Đồ thị của hàm số cho bởi công thức này có tiệm cận đứng là $r=0$ , điều này có nghĩa là khi $r$ dần về $0$ thì lực hấp dẫn sẽ tiến đến

G

.

+\infty

.

C

, với

C

là hằng số nào đó.

0

.

Câu 11 (1đ):

Với giá trị nào dưới đây của $m$ thì hàm số $y=\cos 2x+mx$ đồng biến trên $\mathbb{R}$ ?

m\ge 2

.

m\ge 1

.

m>4

.

m<2

.

Câu 12 (1đ):

Số giá trị nguyên dương của tham số $m$ để đồ thị hàm số $y=\dfrac{x-1}{{{x}^{2}}-8x+m}$ có $3$ đường tiệm cận là

12

.

14

.

16

.

10

.

Câu 13 (1đ):

Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau.

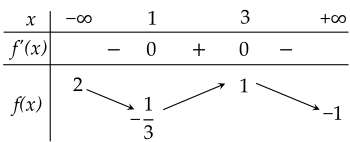
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số có giá trị cực đại bằng $3$ .
b) Hàm số có hai điểm cực trị.
c) Hàm số có giá trị lớn nhất bằng $1$ , nhỏ nhất bằng $-\dfrac{1}{3}$ .
d) Đồ thị hàm số không cắt trục hoành.

Câu 14 (1đ):

Cho hàm số $y=f(x )$ có bảng biến thiên như sau

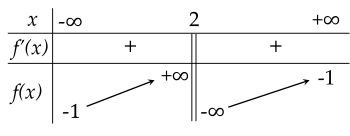
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đồ thị hàm số có đường tiệm cận đứng là $x=2$ .
b) Đồ thị hàm số có đường tiệm cận ngang là $x=-1$ .
c) Tổng số đường tiệm cận của đồ thị hàm số đã cho là $2$ .
d) Hàm số đồng biến trên $\mathbb{R}$ .

Câu 15 (1đ):

Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng $288$ m $^3$ . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là $500\,000$ đồng/m $^2$ . Ba kích thước của bể được mô tả như hình vẽ dưới ( $a$ (m) $>0$ ; $c$ (m) $>0$ ).

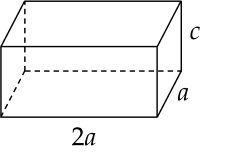
loading...

Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất (Biết độ dày thành bể và đáy bể không đáng kể).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Diện tích các mặt cần xây là $S=2a^2+6ac$ m $^2$ .
b) $2a^2c=280$ .
c) Diện tích các mặt cần xây nhỏ nhất là $216$ m $^2$ .
d) Chi phí thấp nhất để xây dựng bể đó là $108$ triệu đồng.

Câu 16 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

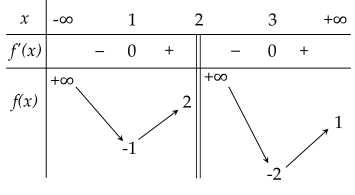
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giá trị nhỏ nhất của hàm số trên $[-2,5 ; 1,5]$ là $-2$ .
b) Hàm số xác định và liên tục trên $\mathbb{R}$ .
c) Điểm cực tiểu của đồ thị hàm số đã cho là $(3;-2)$ .
d) Với $-1\lt m\lt 1$ thì phương trình $f(x)=m$ có $4$ nghiệm phân biệt.

Câu 17 (1đ):

Tại một công ty sản xuất đồ chơi an toàn cho trẻ em, công ty phải chi $40\,000$ USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi $A$ , công ty phải trả $6$ USD cho nguyên liệu ban đầu và nhân công. Gọi $x$ , ( $x \ge 1$ ) là số đồ chơi $A$ mà công ty đã sản xuất và $P(x)$ (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất $x$ đồ chơi $A$ . Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi $A$ là $F(x)=\dfrac{P(x)}{x}$ . Xem $y = F(x)$ là hàm số theo $x$ xác định trên nửa khoảng $\left[ 1;+\infty \right)$ có phương trình đường tiệm cận ngang là $y = b$ . Tính $b$ .

Trả lời:

Câu 18 (1đ):

Biết thể tích $V$ (đơn vị: centimét khối) của $1$ kg nước tại nhiệt độ $T$ , ( $0^\circ$ C $\le T \le 30^\circ$ C) được tính bởi công thức: $V(T) = 999,87 - 0,06426T + 0,0085043T^2 - 0,0000679T^3$ . Thể tích $V(T)$ thấp nhất ở nhiệt độ bao nhiêu? (làm tròn đến hàng đơn vị của đơn vị $^\circ$ C)

Trả lời:

Câu 19 (1đ):

Theo thống kê tại một nhà máy $Z$ , nếu áp dụng tuần làm việc $40$ giờ thì mỗi tuần có $100$ công nhân đi làm và mỗi công nhân làm được $120$ sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm $2$ giờ mỗi tuần thì sẽ có $1$ công nhân nghỉ việc và năng suất lao động giảm $5$ sản phẩm/ $1$ công nhân/ $1$ giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là $P\left( x \right)=\dfrac{95{{x}^{2}}+120x}{4}$ , với $x$ là thời gian làm việc trong một tuần (đơn vị: giờ). Nhà máy cần áp dụng thời gian làm việc mỗi tuần mấy giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?

Trả lời: giờ.

Câu 20 (1đ):

Cho một tấm nhôm hình vuông có cạnh $24$ cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x$ (cm), rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một khối hộp chữ nhật không nắp.

loading...

Tìm $x$ sao cho thể tích khối hộp lớn nhất.

Trả lời:

Câu 21 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ sau:

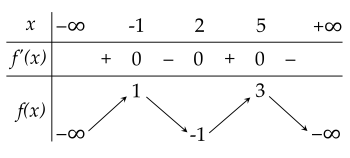
loading...

Phương trình ${f}'\left[5-3f(x)\right]=0$ có bao nhiêu nghiệm thực?

Trả lời:

Câu 22 (1đ):

Cho hàm số $y={f}'(x)$ có đồ thị như hình vẽ.

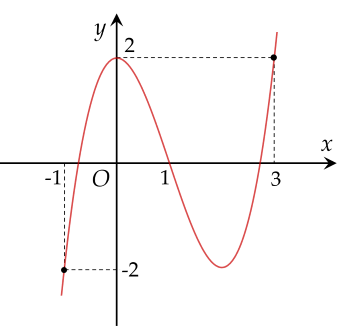
loading...

Hàm số $y=f(x)-\dfrac12(x-1)^2$ nghịch biến trên khoảng $(-\infty ; a)$ . Tìm giá trị nguyên lớn nhất của $a$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP