Đề số 1 - ôn tập chương I: Số tự nhiên (Phần tự luận) SVIP

Hướng dẫn giải:

a. Phân tích theo sơ đồ cây:

Vậy $120 = 2^3.3.5$.​

b. Phân tích theo sơ đồ cột:

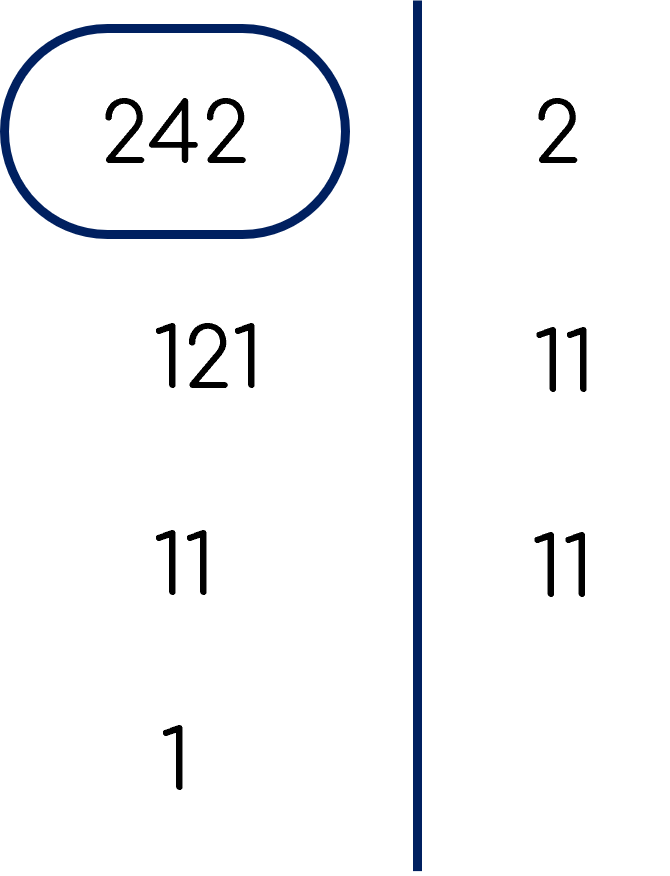
Vậy $242 = 2.11^2$.

Hướng dẫn giải:

Vì mỗi em nhận được phần thưởng như nhau nên số học sinh của tổ 1 là ước chung của $45$ và $36$.

Ta có $45 = 3^2 . 5$ và $36 = 2^2.3^2$.

Suy ra ƯCLN$(45 , 36) = 3^2 = 9$.

Vậy ƯC$(45 , 36) =$ Ư$(9) = \{1; \, 3; \, 9\}$.

Mà số học sinh của mỗi tổ nhiều hơn $5$ nên số học sinh của tố 1 là $9$ em.

Hướng dẫn giải:

Do khi xếp thành hàng $12$, hàng $30$ hay hàng $28$ thì đều vừa đủ hàng nên số học sinh là BC$(12, \, 30, \, 28)$.

Ta có $12 = 2^2 . 3$;

$30 = 2.3.5$;

$28 = 2^2 . 7$.

Suy ra BCNN$(12, \, 30, \, 28) = 2^2.3.5.7 = 420$.

Do đó BC$(12, \, 30, \, 28)$ = B$(420) = \{0; \, 420; \, 840; \, 1 \, 260; \, 1 \, 680; \, 2 \, 100; \, ... \}$.

Mà số học sinh của trường trong khoảng từ $1$ $800$ đến $2$ $500$. Vậy số học sinh của trường đó là $2$ $100$ em.

Hướng dẫn giải:

ƯCLN$(a,b)$ = $12$, ta xét $a = 12.a' (a' \in \mathbb{N})$​;

$b = 12.b' (b' \in \mathbb{N})$​ với $1 < a' < b'$.

Do $12$ là ƯCLN của $a$ và $b$ nên ƯCLN$(a', b') = 1$.

Ta có: 

$180$ ⋮ $\left(12.a'\right)\Rightarrow \left(180:12\right)$ ⋮ $a'\Rightarrow 15$ ⋮ $a'$.

$180$ ⋮ $\left(12.b'\right)\Rightarrow \left(180:12\right)$ ⋮ $b'\Rightarrow 15$ ⋮ $b'$.

Suy ra $a', b'$ là hai ước nguyên tố cùng nhau của $15$.

Dễ thấy, $a' = 3; \, b' = 5$ thỏa mãn điều kiện trên với $1 < a' < b'$ và ƯCLN$(a', b') = 1$.

Vậy $a = 12.3 = 36$ và $b = 12.5 = 60$.