Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 2 (Phần tự luận 7 điểm) SVIP
Tính bằng cách hợp lý (nếu có)
a) ${A}= \dfrac{15}{12}+ \dfrac{5}{13}+ \dfrac{-3}{12}+ \dfrac{-18}{13}$
b) ${B}= \dfrac{11}{15} \cdot \dfrac{-19}{13}+ \dfrac{-7}{13} \cdot \dfrac{11}{15}$
c) ${C}=2022^{0}-\Big( \dfrac{1}{7}\Big)^5 \cdot 7^5$
Hướng dẫn giải:
a) ${A}= \dfrac{15}{12}+ \dfrac{5}{13}+ \dfrac{-3}{12}+ \dfrac{-18}{13}$
$= \Big( \dfrac{15}{12}+\dfrac{-3}{12} \Big) + \Big( \dfrac{5}{13} + \dfrac{-18}{13} \Big)$
$= \Big( \dfrac{12}{12}\Big) + \Big( \dfrac{-13}{13} \Big)$
$= 1 + (-1)=0$
b) ${B}= \dfrac{11}{15} \cdot \dfrac{-19}{13}+ \dfrac{-7}{13} \cdot \dfrac{11}{15}$
$= \dfrac{11}{15} \cdot \Big( \dfrac{-19}{13} + \dfrac{-7}{13} \Big)$
$= \dfrac{11}{15} \cdot ( -2 )$
$= \dfrac{-22}{15}$
c) ${C}=2022^{0}-\Big( \dfrac{1}{7}\Big)^5 \cdot 7^5$
$=1-\dfrac{1}{7^5} \cdot 7^5$
$=1-1 = 0$
Tìm $x$, biết:
$a)$ $\dfrac{7}{4} x- \dfrac{3}{2}=- \dfrac{4}{5}$
$b)$ $\Big(x- \dfrac{1}{4}\Big)^2= \dfrac{5}{36}-\Big( \dfrac{1}{3}\Big)^2$
$c)$ $- x + \dfrac{3}{2}=x+\dfrac{3}{5}$
Hướng dẫn giải:
$a)$ $\dfrac{7}{4} \cdot x- \dfrac{3}{2}=- \dfrac{4}{5}$
$ \dfrac{7}{4} \cdot x = - \dfrac{4}{5} + \dfrac{3}{2}$
$ \dfrac{7}{4} \cdot x = \dfrac{7}{10}$
$ x = \dfrac{7}{10} :\dfrac{7}{4}$
$ x = \dfrac{2}{5}$
$b)$ $\Big(x- \dfrac{1}{4}\Big)^2= \dfrac{5}{36}-\Big( \dfrac{1}{3}\Big)^2$
$\Big(x- \dfrac{1}{4}\Big)^2= \dfrac{5}{36}-\dfrac{1}{9}$
$\Big(x- \dfrac{1}{4}\Big)^2= \dfrac{1}{36}$
$x- \dfrac{1}{4}= \dfrac{1}{6}$ hoặc $x- \dfrac{1}{4}= -\dfrac{1}{6}$
$x= \dfrac{5}{12}$ hoặc $x= \dfrac{1}{12}$
$c)$ $-x + \dfrac{3}{2}=x+\dfrac{3}{5}$
$-x -x =\dfrac{3}{5}- \dfrac{3}{2}$
$-2x =-\dfrac{9}{10}$
$x =\dfrac{9}{20}$
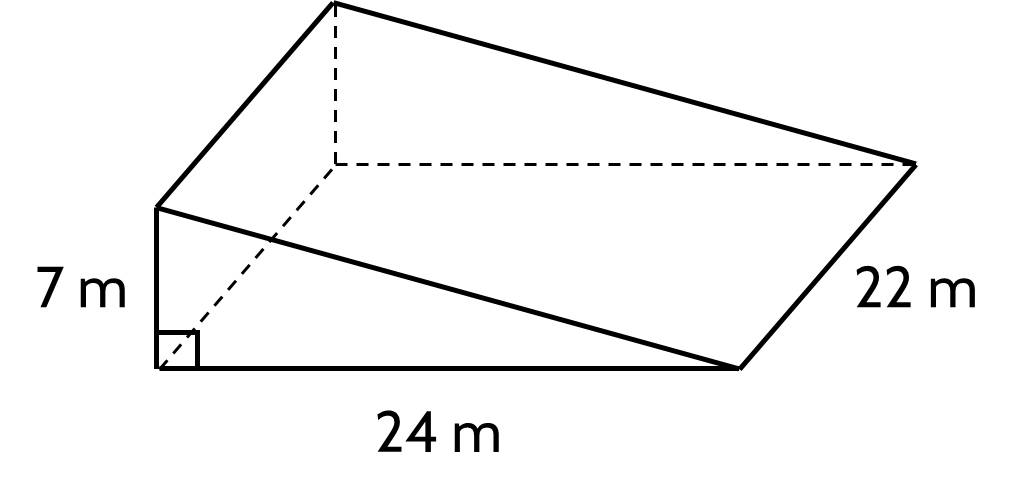
Để làm đường dẫn lên cầu bắc qua một con kênh, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như hình vẽ. Hãy tính thể tích của khối bê tông.
Hướng dẫn giải:
Diện tích đáy của tam giác là:
$\dfrac{1}{2}.7.24 = 84$ ($m^2$)
Thể tích của khối bê tông là:
$84 . 22 = 1\,848$ ($m^3$)
Một cửa hàng có $120$ kg đường và bán hết trong $3$ ngày. Ngày thứ nhất cửa hàng bán được $25 \%$ số đường. Ngày thứ hai cửa hàng bán được $\dfrac{4}{9}$ số đường còn lại. Tính khối lượng đường bán ra trong ngày thứ ba.
Hướng dẫn giải:
Ngày thứ nhất bán được số kg đường là:
$120 . 25\% = 30$ (kg đường)
Sau ngày thứ nhất, số đường còn lại là:
$120 - 30 = 90$ (kg)
Ngày thứ hai bán được số kg đường là:
$90.\dfrac{4}{9}=40$ (kg)
Ngày thứ ba bán được số kg đường là:
$120 - 30 - 40=50$ (kg)
Đáp số: $50$ kg.
Cho $S=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\ldots . .+\dfrac{1}{3^{2\,021}}+\dfrac{1}{3^{2\,022}}$.
Chứng minh $S<\dfrac{1}{2}$.
Hướng dẫn giải:
Ta có $3S=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...++\dfrac{1}{3^{2\,021}}$.
$3S-S =\Big( 1+\dfrac{1}{3}+\dfrac{1}{3^2}+...++\dfrac{1}{3^{2\,021}} \Big) - \Big( \dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\ldots . .+\dfrac{1}{3^{2\,021}}+\dfrac{1}{3^{2\,022}} \Big)$
$=1 - \dfrac{1}{3^{2\,022}}$
$3S-S=1 - \dfrac{1}{3^{2\,022}}$
$S=\dfrac{1}{2} - \dfrac{1}{2.3^{2\,022}}$
Vậy $S<\dfrac{1}{2}$.
