Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 5 (thời gian: 90 phút) SVIP
(2,0 điểm) Giải các phương trình sau:
a) $4x-5=0$;
b) $2x+1=7-x$;
c) $(x+2)(x-3)=0$;
d) \(\dfrac{x-3}{x+1}=\dfrac{x^2}{x^2-1}\).
Hướng dẫn giải:
a) \(3x-12=0\Leftrightarrow3x=12\Leftrightarrow x=4\).
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{4\right\}\).
b) \(2x+1=7-x\Leftrightarrow2x+x=7-1\Leftrightarrow3x=6\Leftrightarrow x=2\).
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{2\right\}\).
c) \(\left(x-2\right)\left(2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{-\dfrac{3}{2};2\right\}\).
d) \(\dfrac{x-3}{x+1}=\dfrac{x^2}{x^2-1}\) (đk: \(x\ne\pm1\))
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{x^2}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow\left(x-3\right)\left(x-1\right)=x^2\)
\(\Leftrightarrow x^2-4x+3=x^2\)
\(\Leftrightarrow-4x+3=0\)
\(\Leftrightarrow x=\dfrac{3}{4}\) (thỏa mãn)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{\dfrac{3}{4}\right\}\).
(2,0 điểm) Cho phương trình \(m^2x+6\left(x+1\right)=m\left(5x+3\right)\) ($m$ là tham số) (1)
a) Giải phương trình (1) khi $m=1$.
b) Tìm $m$ để phương trình (1) có một nghiệm duy nhất thỏa mãn biểu thức \(A=\dfrac{x^2+2x+3}{x^2+2}\) đạt giá trị nhỏ nhất.
Hướng dẫn giải:
a) Thay $m=1$ vào phương trình (1) ta được:
\(x+6\left(x+1\right)=5x+3\)
\(\Leftrightarrow x+6x+6=5x+3\)
\(\Leftrightarrow2x=-3\)
\(\Leftrightarrow x=\dfrac{-3}{2}\).
Vậy với $m=1$ phương trình đã cho có tập nghiệm là \(S=\left\{-\dfrac{3}{2}\right\}\).
b) Ta có:
\(A=\dfrac{x^2+2x+3}{x^2+2}=\dfrac{\dfrac{1}{2}\left(x^2+2\right)+\dfrac{1}{2}\left(x^2+4x+4\right)}{x^2+2}=\dfrac{1}{2}+\dfrac{1}{2}.\dfrac{\left(x+2\right)^2}{x^2+2}\ge\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(x+2=0\Leftrightarrow x=-2\).
Vậy giá trị nhỏ nhất của \(A\) là \(\dfrac{1}{2}\) đạt tại \(x=-2\).
Ta cần tìm $m$ để phương trình (1) có nghiệm duy nhất $x=-2$.
Thế $x=-2$ vào phương trình (1) ta được:
\(m^2.\left(-2\right)+6\left(-2+1\right)=m\left[5.\left(-2\right)+3\right]\)
\(\Leftrightarrow2m^2-7m+6=0\)
\(\Leftrightarrow2m^2-3m-4m+6=0\)
\(\Leftrightarrow m\left(2m-3\right)-2\left(2m-3\right)=0\)
\(\Leftrightarrow\left(m-2\right)\left(2m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\2m-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=\dfrac{3}{2}\end{matrix}\right.\).
Với \(m=2\) phương trình (1) trở thành:
\(4x+6\left(x+1\right)=2\left(5x+3\right)\)
\(\Leftrightarrow0x=0\).
Phương trình này có vô số nghiệm (loại).
Với \(m=\dfrac{3}{2}\) phương trình (1) trở thành:
\(\dfrac{9}{4}x+6\left(x+1\right)=\dfrac{3}{2}\left(5x+3\right)\)
\(\Leftrightarrow\dfrac{3}{4}x=-\dfrac{3}{2}\Leftrightarrow x=-2\) (thỏa mãn).
Vậy \(m=\dfrac{3}{2}\) thỏa mãn ycbt.
(2,0 điểm) Giải bài toán sau bằng cách lập phương trình
Một xe máy đi từ $A$ đến $B$ với vận tốc $40 \mathrm{~km} / \mathrm{h}$. Đến $B$ người đó nghỉ $10$ phút rồi quay về $A$ với vận tốc $30 \mathrm{~km} / \mathrm{h}$. Biết thời gian tổng cộng hết $3$ giờ $40$ phút. Tính quãng đường $AB$.
Hướng dẫn giải:
Gọi độ dài quãng đường $AB$ là $x$ ($\mathrm{km}$), $x>0$.
Thời gian xe máy đi từ $A$ đến $B$ là \(\dfrac{x}{40}\) giờ.
Thời gian xe máy đi từ $B$ về $A$ là \(\dfrac{x}{30}\) giờ.
Tổng thời gian đi của người đó là:
$3$ giờ $40$ phút $-10$ phút $=3$ giờ $30$ phút $=3,5$ giờ.
Ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{30}=3,5\Leftrightarrow30x+40x=3,5.40.30\Leftrightarrow x=60\) (thỏa mãn)
Vậy độ dài quãng đường $AB$ là $60 \mathrm{~km}$.
(3,0 điểm) Cho hình chữ nhật $MNPQ$ có $MN =8 \mathrm{~cm}$, $MQ=6 \mathrm{~cm}$. Gọi $K$ là chân đường vuông góc kẻ từ $N$ xuống $MP$, phân giác của góc $MQP$ cắt $MP$ ở $I$.
a) Chứng minh: $\triangle KMN \backsim \triangle QPM$.
b) Tính $MK$, $KN$.
c) Chứng minh $MI.MK=PI.KN$.
Hướng dẫn giải:
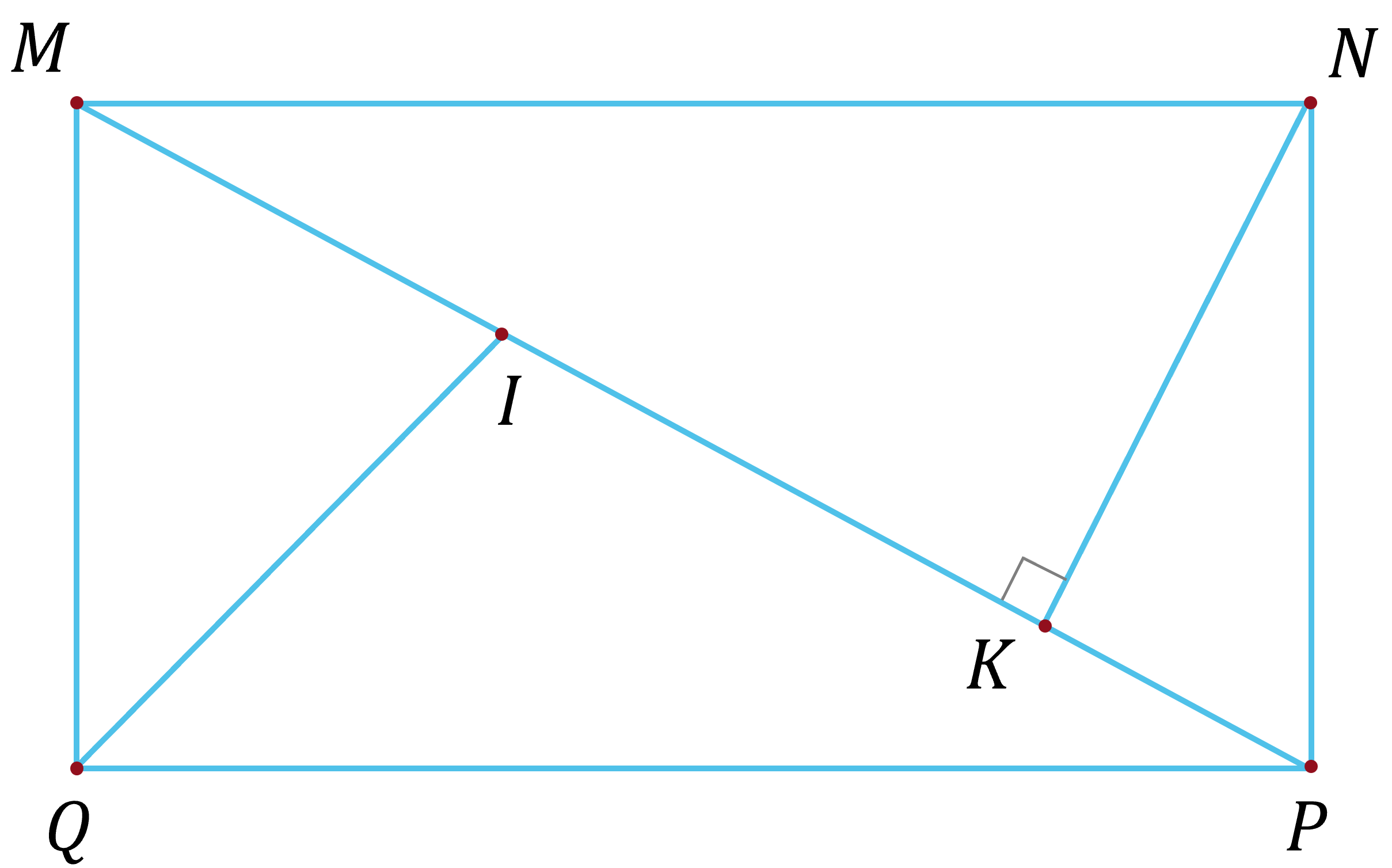
a) Chứng minh: $\triangle KMN \backsim \triangle QPM$
Xét $\triangle KMN$ và $\triangle QPM$ có:
$\widehat{MKN} = \widehat{MQP} =90^\circ$
$\widehat{KMN} = \widehat{QPM}$ ($MN \parallel PQ$, hai góc so le trong)
suy ra $\triangle KMN \backsim \triangle QPM$ (g.g)
b) Tính $MK$, $KN$
Sử dụng định lí Pythagoras dễ dàng tính được $MP =10 \mathrm{~cm}$.
Vì $\triangle KMN \backsim \triangle QPM$ do đó
\(\dfrac{KM}{QP}=\dfrac{MN}{PM}=\dfrac{KN}{QM}\) hay \(\dfrac{KM}{8}=\dfrac{KN}{6}=\dfrac{8}{10}\)
suy ra $KM=6,4 \mathrm{~cm}$; $KN=4,8 \mathrm{~cm}$.
c) Chứng minh $MI.MK=PI.KN$
Ta có: \(\dfrac{KN}{QM}=\dfrac{KM}{QP}\Leftrightarrow\dfrac{KN}{KM}=\dfrac{QM}{QP}\).
Lại có $QI$ là đường phân giác trong tam giác $QPM$ suy ra \(\dfrac{IM}{IP}=\dfrac{QM}{QP}\).
Do đó \(\dfrac{KN}{KM}=\dfrac{IM}{IP}\Leftrightarrow MI.MK=PI.KN\).
(1,0 điểm)
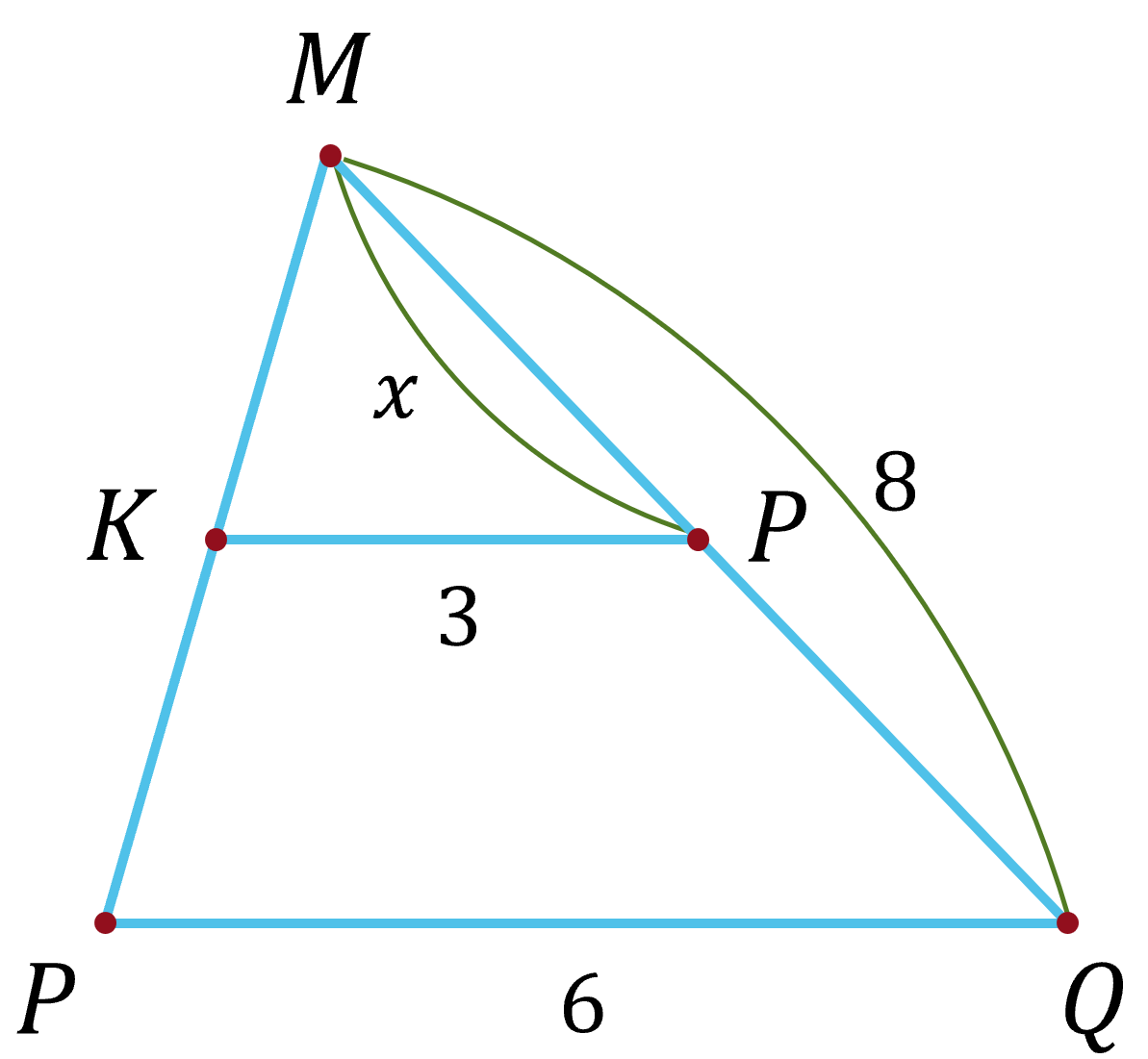
a) Cho $KP \parallel NQ$. Tính độ dài $x$ trong hình dưới đây.
b) Cho hình thang $ABCD$ ($AB \parallel CD$). Điểm $E$ thuộc cạnh $AD$, điểm $F$ thuộc cạnh $BC$ sao cho \(\dfrac{DE}{DA}=\dfrac{BF}{BC}=\dfrac{1}{3}\). Gọi $M$, $N$ theo thứ tự là giao điểm của $EF$ với $BD$, $AC$. Chứng minh rằng $EM=NF$.
Hướng dẫn giải:
a) Vì $KP \parallel NQ$ nên \(\dfrac{3}{6}=\dfrac{x}{8}\Leftrightarrow x=4\).
b) Chứng minh $EM=NF$
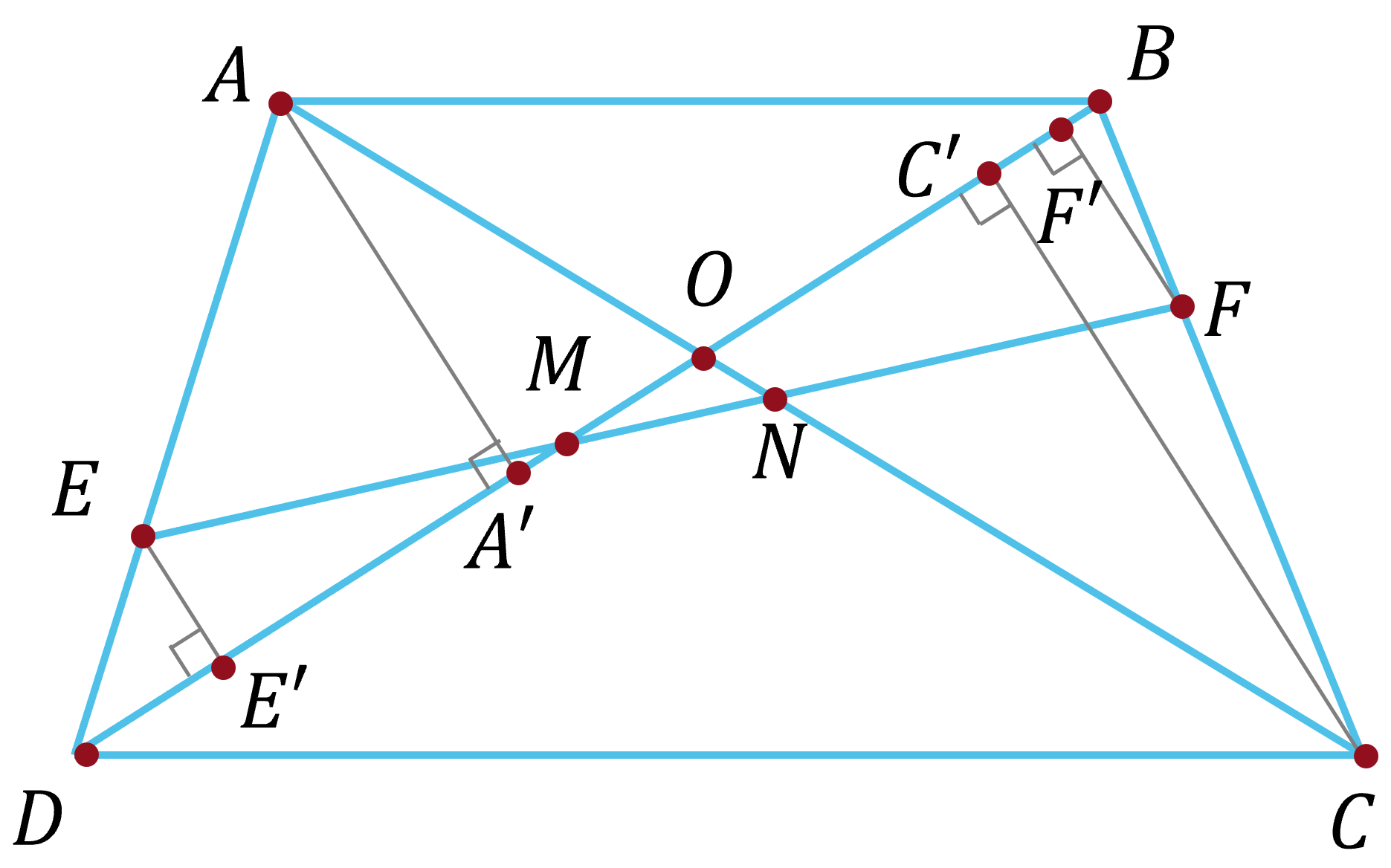
Kẻ \(AA',CC',EE',FF'\) vuông góc với $BD$. Gọi $O$ là giao điểm của $AC$ và $BD$.
Ta có \(\dfrac{EM}{MF}=\dfrac{EE'}{FF'}=\dfrac{\dfrac{1}{3}AA'}{\dfrac{1}{3}CC'}=\dfrac{AA'}{CC'}=\dfrac{OA}{OC}\)
Tương tự ta cũng có \(\dfrac{FN}{NE}=\dfrac{OB}{OD}\).
mà \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\) suy ra \(\dfrac{EM}{MF}=\dfrac{FN}{NE}\Rightarrow\dfrac{EM}{MF+EM}=\dfrac{FN}{NE+FN}\)
\(\Leftrightarrow\dfrac{EM}{EF}=\dfrac{FN}{EF}\) hay $EM = FN$.
