Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Lượng điện tiêu thụ mỗi ngày trong 7 ngày đầu tháng 02/2023 của một hộ gia đình được cho ở biểu đồ sau:
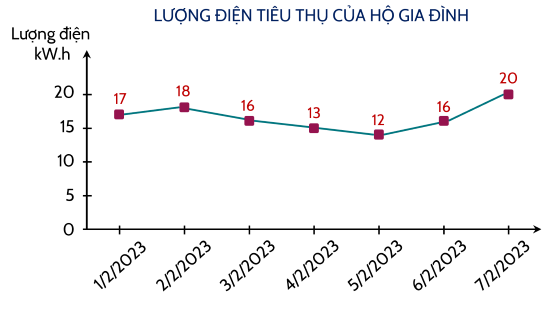
a) Ngày nào trong tuần đầu tiên của tháng 02/2023, hộ gia đình tiêu thụ lượng điện it nhất?
b) Trong tuần đầu tiên của tháng 02/2023, hộ gia đình đó tiêu thụ hết bao nhiêu kW.h điện? Trung bình mỗi ngày tiêu thụ bao nhiêu kW.h điện?
c) Trong 7 ngày đầu tiên của tháng 02/2023, ngày tiêu thụ điện nhiều nhất tăng bao nhiêu $\%$ so với ngày tiêu thụ điện it nhất?
Hướng dẫn giải:
a) Ngày 5/2/2023.
b) Tổng lượng điện tiêu thụ trong tuần đầu tháng 2/2023 là:
17 + 18 + 16 + 13 + 12 + 16 + 20 = 112 (kW.h)
Trung bình mỗi ngày trong tuần đó, gia đình tiêu thụ:
112 : 7 = 16 (kW.h)
c) Ngày 7/2 tiêu thụ điện nhiều nhất: 20 KW.h
Ngày 5/2 tiêu thụ điện ít nhất: 12 kW.h
Trong 7 ngày đầu tiên của tháng 02/2023, ngày tiêu thụ điện nhiều nhất tăng so với ngày tiêu thụ điện it nhất là:
(20 - 12) : 12 . 100% = 66,7%.
Một nhóm học sinh quốc tế gồm $9$ học sinh đến từ các nước: Mỹ, Anh, Pháp, Thái Lan, Việt Nam, Canada, Thụy Sĩ, Nga và Brasil; mỗi nước chỉ có đúng một học sinh. Chọn ra ngẫu nhiên một học sinh trong nhóm học sinh trên.
a) Tìm số phần tử của tập hợp ${G}$ gồm các kết quả có thể xảy ra đối với học sinh được chọn ra.
b) Tính xác suất của biến cố: "Học sinh được chọn ra đến từ châu Á".
Hướng dẫn giải:
a) Tập hợp các kết quả có thể xảy ra đối với học sinh được chọn ra là:
$G = \{$Mỹ; Anh; Pháp; Thái Lan; Việt Nam; Canada; Thụy Sĩ; Nga; Brasil$\}$.
Số phần tử của tập hợp ${G}$ là $9$.
b) Trong $9$ nước trên có các nước thuộc châu Á là: Việt Nam và Thái Lan.
Do đó có $2$ kết quả thuận lợi cho biến cố "Học sinh được chọn ra đến từ châu Á" là: Việt Nam; Thái Lan.
Khi đó xác suất của biến cố "Học sinh được chọn ra đến từ châu Á" bằng: $\dfrac29$.
Cho tam giác $ABC$ cân tại $A$. Tia phân giác của góc $B$ cắt $AC$ tại $F$, tia phân giác của góc $C$ cắt $AB$ tại $E$.
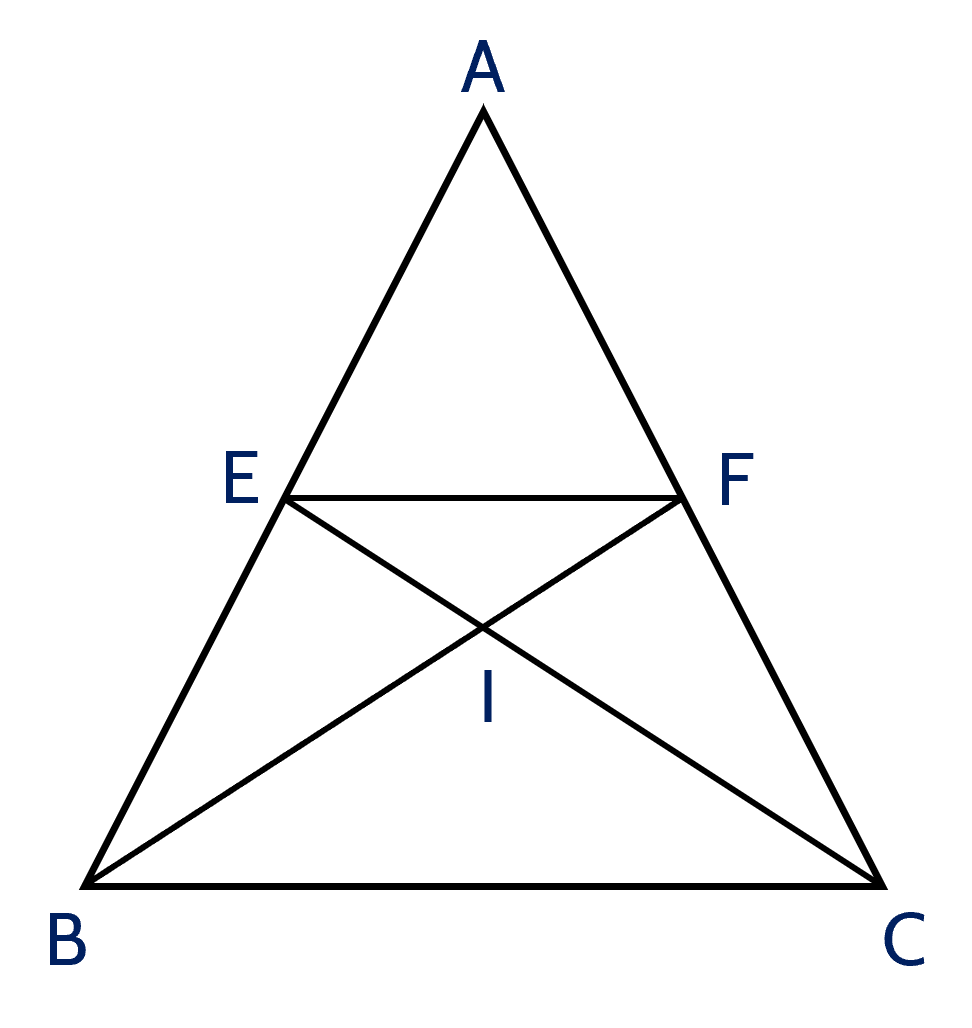
a) Chứng minh rằng $\widehat{A B F}=\widehat{A C E}$.
b) Chứng minh rằng tam giác $AEF$ cân.
c) Gọi I là giao điểm của $BF$ và $CE$. Chứng minh rằng tam giác $IBC$ và tam giác $IEF$ là những tam giác cân.
Hướng dẫn giải:
a) Do tam giác ${ABC}$ cân tại ${A}$ nên ${AB}={AC}$ và $\widehat{A B C}=\widehat{A C B}$.
Do $BF$ là tia phân giác của $\widehat{A B C}$ nên $\widehat{A B F}=\widehat{F B C}=\dfrac{1}{2} \widehat{A B C}$.
Do $CE$ là tia phân giác của $\widehat{A C B}$ nên $\widehat{A C E}=\widehat{E C B}=\dfrac{1}{2} \widehat{A C B}$.
Do đó $\widehat{A B F}=\widehat{A C {E}}$.
b) Xét $\triangle A B F$ và $\triangle A C E$ có:
$\widehat{A B F}=\widehat{A C E}$ (chứng minh trên).
$A B=A C$ (chứng minh trên).
$\widehat{A}$ chung.
Do đó $\triangle A B F=\triangle A C {E}$ (g.c.g).
Suy ra ${AF}={AE}$ (hai cạnh tương ứng).
Tam giác ${AEF}$ có ${AF}={AE}$ nên tam giác ${AEF}$ cân tại ${A}$.
c) Ta có $\widehat{F B C}=\widehat{E C B}$ nên $\widehat{I B C}=\widehat{I C B}$.
Tam giác $IBC$ có $\widehat{I B C}=\widehat{I C B}$ nên tam giác $IBC$ cân tại $I$.
Do đó ${IB}={IC}$.
$\widehat{E I B}=\widehat{F I C}$ (đối đỉnh).
${IB}={IC}$ (chứng minh trên).
$\widehat{E B I}=\widehat{F C I}$ (chứng minh trên).
Do đó $\Delta E I B=\Delta F I C$ (g.c.g).
Suy ra $IE = IF$ (hai cạnh tương ứng).
Tam giác $IEF$ có $IE = IF$ nên tam giác $IEF$ cân tại $I$.
