Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) $\dfrac x{-3} = \dfrac74$

$x = \dfrac{7.(-3)}4$

$x = \dfrac{-21}4$.

b) $\dfrac{x + 9}{15 - x} = \dfrac23$

$(15 - x).2 = (x + 9).3$

$30 - 2x = 3x + 27$

$5x = 3$

$x = \dfrac35$.

Hướng dẫn giải:

Từ $2x = 5y$ ta suy ra $\dfrac x5 = \dfrac y2$.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\dfrac x5 = \dfrac y2 = \dfrac{3x}{15} = \dfrac{4y}{8} = \dfrac{3x + 4y}{15 + 8} = \dfrac{46}{23} = 2$

Suy ra $x = 2.5 = 10$;

$y = 2.2 = 4$.

Hướng dẫn giải:

Gọi số máy cày của ba đội lần lượt là $x$, $y$, $z$ (máy).

Vì diện tích cày là như nhau nên số máy cày và thời gian là hai đại lượng tỉ lệ nghịch.

Nên $x.5 = y.6 = z.8 \Rightarrow \dfrac x{24} = \dfrac y{20} = \dfrac z{15}$.

Đội thứ hai có nhiều hơn đội thứ ba $5$ máy nên $y - z = 5$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\dfrac x{24} = \dfrac y{20} = \dfrac z{15} = \dfrac{y-z}{20 - 15} = \dfrac55 = 1$

Suy ra $x = 24$; $y = 20$; $z = 15$.

Hướng dẫn giải:

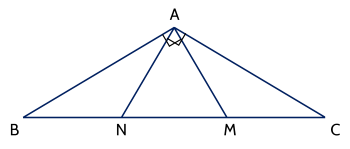
a) Do $MA \perp AB$ và $NA \perp AC$ nên $\widehat{BAM} = \widehat{CAN} = 90^{\circ}$.

Tam giác $ABC$ cân tại $A$ nên $AB = AC$ và $\widehat{ABC} = \widehat{ACB}$.

Xét hai tam giác $BAM$ và $CAN$ có:

     $\widehat{ABM} = \widehat{ACN}$;

     $AB = AC$ (cmt);

     $\widehat{BAM} = \widehat{CAN}$;

Vậy $\Delta BAM = \Delta CAN$ (g.c.g).

b) $\Delta BAM = \Delta CAN$ suy ra $BM = CN$ (hai cạnh tương ứng).

Mà $BM = BN + NM$ và $CN = CM + MN$.

Suy ra $BN = CM$.

c) Xét tam giác $ABC$ có: $\widehat{A B C}+\widehat{A C B}+\widehat{B A C}=180^{\circ}$.

Mà $\widehat{A B C}=\widehat{A C B}$ nên $2 \widehat{A B C}=180^{\circ}-\widehat{B A C}=180^{\circ}-120^{\circ}=60^{\circ}$.

Do đó $\widehat{A B C}=\widehat{A C B}=30^{\circ}$.

Do $\triangle B A M=\triangle C A N$ (cmt) nên ${AM}={AN}$ (hai cạnh tương ứng).

Do đó tam giác $AMN$ cân tại $A$ (1).

Xét tam giác $CAN$ vuông tại $A$ có $\widehat{A N C}+\widehat{A C N}=90^{\circ}$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $\widehat{A N C}=90^{\circ}-\widehat{A C N}=90^{\circ}-30^{\circ}=60^{\circ}$ (2).

Từ (1) và (2) suy ra tam giác $AMN$ đều.

Do đó $\widehat{M A N}=60^{\circ}$.

Ta có: $\widehat{M A N}+\widehat{N A B}=\widehat{M A B}$.

Suy ra $\widehat{N A B}=\widehat{M A B}-\widehat{M A N}=90^{\circ}-60^{\circ}=30^{\circ}$.

Do đó $\widehat{N A B}=\widehat{A B N}=30^{\circ}$.

Suy ra tam giác $ANB$ cân tại $N$.