Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Tìm số hữu tỉ $x$ trong các tỉ lệ thức sau:
a) $\dfrac{x}{6}=\dfrac{-3}{4}$;
b) $\dfrac{5}{x}=\dfrac{15}{-20}$;
c) $\dfrac{x+11}{14-x}=\dfrac{2}{3}$.
Hướng dẫn giải:
a) $\dfrac{x}{6}=\dfrac{-3}{4}$
$x=\dfrac{(-3) .6}{4}$
$x=\dfrac{-9}{2}$
Vậy $x=\dfrac{-9}{2}$.
b) $\dfrac{5}{x}=\dfrac{15}{-20}$
$x=\dfrac{5 .(-20)}{15}$
$x=\dfrac{-20}{3}$
Vậy $x=\dfrac{-20}{3}$.
c) $3(x+11)=2(14-x)$
$3x + 33 = 28-2x$
$3x + 2x = 28-33$
$5x =-5$
$x =-1$
Vậy $x=-1$.
Cho đa thức $Q(x)=6x+3x^2-9$.
a) Sắp xếp đa thức $Q(x)$ theo lũy thừa giảm dần của biến.
b) Tính giá trị của $Q(x)$ khi $x=3$.
c) Cho $x \in \{1 ; 3 ;-3\}$, giá trị nào của $x$ là nghiệm của đa thức ${Q}( {x})$?
Hướng dẫn giải:
a) ${Q}( {x})=3 x^2+6 x-9$.
b) $Q(3)=3 .3^2+6.3-9=36$.
c) Ta thấy $Q(-1) = Q(-3) =0$ nên $x=1$ và $x=-3$ là nghiệm của $Q(x)$.
Tìm hai số $a, b$ biết rằng $2a = 5b$ và $3a + 4b = 46$.
Hướng dẫn giải:
Ta có: $2a=5b$
Suy ra $\dfrac{a}{5}=\dfrac{b}{2}$.
Lại có: $\dfrac{a}{5}=\dfrac{3a}{15};\dfrac{b}{2}=\dfrac{4b}{8}$.
Suy ra $\dfrac{3a}{15}=\dfrac{4b}{8}=\dfrac{3a+4b}{15+8}=\dfrac{46}{23}=2$
$\dfrac{a}{5}=2$ suy ra $a=10$.
$\dfrac{b}{2}=2$ suy ra $b=4$.
Trong đợt quyên góp sách ủng hộ các bạn vùng cao, số sách mà ba lớp 7A, 7B, 7C quyên góp được tỉ lệ với ba số $5; 6; 8$. Tính số sách cả mỗi lớp đã quyên góp, biết số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là $24$ quyển.
Hướng dẫn giải:
Gọi số sách 3 lớp 7A, 7B, 7C quyên góp được là ${x}, {y}, {z}$ (quyển) $(x, y, z \in \mathbb{N} ^*$ ).
Vì số sách mà ba lớp 7A,7B,7C quyên góp được tỉ lệ với ba số $5;6;8$ nên $\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{8}$.
Mà số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là $24$ quyển nên $z-x=24$.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
$\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{8}=\dfrac{z-x}{8-5}=\dfrac{24}{3}=8$
$\Rightarrow x=5.8=40 ; y=6.8=48; z=8.8=64$
Vậy số sách 3 lớp 7A,7B,7C quyên góp được lần lượt là $40$ quyển; $48$ quyển và $64$ quyển.
Cho tam giác $ABC (AB < AC), M$ là trung điểm của $BC$. Trên tia đối của tia $MA$ lấy điểm $E$ sao cho $AM = EM.$
a. Chứng minh: $\Delta AMB = \Delta EMC$.
b. Từ $A$ kẻ $AH$ vuông góc với $BC$. Trên tia đối của tia $HA$ lấy điểm $D$ sao cho $HA = HD$. Chứng minh: $CE = BD$.
c. Tam giác $AMD$ là tam giác gì? Vì sao?
Hướng dẫn giải:
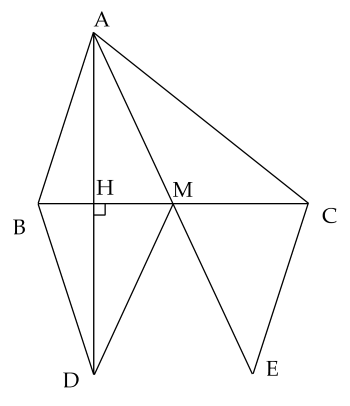
a. Xét tam giác $ABM$ và tam giác $MEC$ có:
$BM = MC$ ($M$ là trung điểm $BC$)
$\widehat{AMB}=\widehat{CME}$(đối đỉnh)
$AM = ME$ (gt)
Suy ra $\Delta AMB = \Delta EMC$ (c.g.c)
b. Xét tam giác $ABH$ vuông tại $H$ và tam giác $BHD$ vuông tại $H$ có:
$BH$ là cạnh chung
$AH = DH$ (gt)
Suy ra $\Delta ABH = \Delta DBH$ (c.g.c)
Suy ra $AB = BD$ (cặp cạnh tương ứng) (1)
Ta lại có: $\Delta AMB = \Delta EMC$ (cmt) suy ra $AB = CE$ (2).
Từ (1) và (2) suy ra $CE = BD.$
c. Vì $\Delta ABH = \Delta DBH$ nên $AH = DH$ (cặp cạnh tương ứng).
Xét $\Delta AHM$ và $\Delta DHM$ đều vuông tại $H$:
$AH = DH$
Chung cạnh $HM$
Suy ra $\Delta AHM = \Delta DHM$ (c.g.c).
Suy ra $AM=DM$ (cặp cạnh tương ứng).
Vậy tam giác $AMD$ là tam giác cân tại $M.$
