Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Nội dung đề thi (120 phút) SVIP
a) Rút gọn biểu thức: $A=\sqrt{28}+\sqrt{63}-2 \sqrt{7}$
b) Chứng minh rằng: $\dfrac{x \sqrt{y}+y \sqrt{x}}{\sqrt{x y}}: \dfrac{1}{\sqrt{x}-\sqrt{y}}=x-y$ với $x>0 ; y>0 ; x \neq y$
Hướng dẫn giải:
a) Rút gọn biểu thức: $A=\sqrt{28}+\sqrt{63}-2 \sqrt{7}$
$A=\sqrt{28}+\sqrt{63}-2 \sqrt{7}=2 \sqrt{7}+3 \sqrt{7}-2 \sqrt{7}=3 \sqrt{7}$
b) Chứng minh rằng: $\dfrac{x \sqrt{y}+y \sqrt{x}}{\sqrt{x y}}: \dfrac{1}{\sqrt{x}-\sqrt{y}}=x-y$ với $x>0 ; y>0 ; x \neq y$
$\dfrac{x \sqrt{y}+y \sqrt{x}}{\sqrt{x y}}: \dfrac{1}{\sqrt{x}-\sqrt{y}}=\dfrac{\sqrt{x y}(\sqrt{x}+\sqrt{y})}{\sqrt{x y}} \cdot(\sqrt{x}-\sqrt{y})=(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})=x-y$
Vậy $\dfrac{x \sqrt{y}+y \sqrt{x}}{\sqrt{x y}}: \dfrac{1}{\sqrt{x}-\sqrt{y}}=x-y$ với $x>0 ; y>0 ; x \neq y$.
a) Giải hệ phương trình: $\left\{\begin{array}{l}x-2 y=5 \\ 2 x-y=7\end{array}\right.$
b) Cho hàm số: $y=-\dfrac{1}{4} x^{2}$ có đồ thị $(\mathrm{P})$ và đường thẳng $(\mathrm{d})$ : $y=\dfrac{1}{2} x-2$. Vẽ đồ thị (P) và tìm tọa độ giao điểm của $(\mathrm{P})$ với đường thẳng $(\mathrm{d})$ bằng phép tính.
Hướng dẫn giải:
a) Giải hệ phương trình: $\left\{\begin{array}{l}x-2 y=5 \\ 2 x-y=7\end{array}\right.$
$
\left\{\begin{array} { l }
{ x - 2 y = 5 } \\
{ 2 x - y = 7 }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ 2 x - 4 y = 1 0 } \\
{ 2 x - y = 7 }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ 3 y = - 3 } \\
{ 2 x - y = 7 }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ y = - 1 } \\
{ 2 x = 7 + ( - 1 ) }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
y=-1 \\
x=3
\end{array} \text { Vậy } S=\{(3 ;-1)\}\right.\right.\right.\right.\right.
$
b)$+$ Vẽ (P):
| $x$ | $-4$ | $-2$ | $0$ | $2$ | $4$ |
| $y=-\dfrac{1}{4} x^2$ | $-4$ | $-1$ | $0$ | $-1$ | $-4$ |

$+$ Hoành độ giao điểm của $(P)$ và $(d)$ là nghiệm của pt:
$\dfrac{1}{2} x-2=-\dfrac{1}{4} x^{2} \Leftrightarrow \dfrac{1}{4} x^{2}+\dfrac{1}{2} x-2=0 \Leftrightarrow x^{2}+2 x-8=0$
$\Leftrightarrow x^{2}-2 x+4 x-8=0 \Leftrightarrow(x-2)(x+4)=0 \Leftrightarrow\left[\begin{array}{l}x=2 \\ x=-4\end{array}\right.$
Với $x=2$ ta được $y=-1$; với $x=-4$ ta được $y=-4$.
Vậy tọa độ giao điểm của $(P)$ và $(d)$ là : $(2 ;-1)$ và $(-4 ;-4)$.
Cho phương trình: $x^{2}-(m+2) x+m+1=0(1)$
a) Giải phương trình (1) với $m=-3$.
b) Chứng tỏ phương trình (1) luôn có nghiệm với mọi số thực $m$.
c) Tìm $\mathrm{m}$ để phương trình có hai nghiệm phân biệt $x_{1} ; x_{2}$ là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài đường cao ứng với cạnh huyền là $h=\dfrac{2}{\sqrt{5}}$.
Hướng dẫn giải:
a) Giải phương trình (1) vói $m=-3$.
Khi $m=-3$ pt (1) trở thành : $x^{2}+x-2=0$. Vì $1+1+(-2)=0$ nên pt có hai nghiệm $x_{1}=1 ; x_{2}=-2$
b) Chứng tỏ phương trình (1) luôn có nghiệm vói mọi số thực m.
Ta có: $\Delta=[-(m+2)]^{2}-4(m+1)=m^{2}+4 m+4-4 m-4=m^{2} \geq 0$ với mọi $m$
Vậy phương trình (1) luôn có nghiệm với mọi số thực m.
c) Tìm $\mathbf{m}$ để phương trình có hai nghiệm phân biệt $x_{1} ; x_{2}$ là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài đường cao ứng với cạnh huyền là $h=\dfrac{2}{\sqrt{5}}$.
Theo câu b ta có: $\Delta=m^{2}$
Phương trình (1) có có hai nghiệm phân biệt $x_{1} ; x_{2}$ là độ dài hai cạnh góc vuông của một tam giác vuông $\Leftrightarrow\left\{\begin{array}{l}\Delta>0 \\ x_{1}+x_{2}>0 \\ x_{1} \cdot x_{2}>0\end{array} \Leftrightarrow\left\{\begin{array}{l}m^{2}>0 \\ m+2>0 \\ m+1>0\end{array} \Leftrightarrow\left\{\begin{array}{l}m \neq 0 \\ m>-1\end{array}\right.\right.\right.$
Mặt khác tam giác vuông có đường cao ứng với cạnh huyền $h=\dfrac{2}{\sqrt{5}}$ nên áp dụng hệ thức $\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}=\dfrac{1}{h^{2}}$ ta có: $\dfrac{1}{x_{1}^{2}}+\dfrac{1}{x_{2}^{2}}=\dfrac{1}{\left(\dfrac{2}{\sqrt{5}}\right)^{2}} \Leftrightarrow \dfrac{x_{1}^{2}+x_{2}^{2}}{x_{1}^{2} x_{2}^{2}}=\dfrac{5}{4} \Leftrightarrow 4\left[\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}\right]=5\left(x_{1} x_{2}\right)^{2}$ $\Leftrightarrow 4\left[(m+2)^{2}-2(m+1)\right]=5(m+1)^{2} \Leftrightarrow m^{2}+2 m-3=0 \Leftrightarrow\left[\begin{array}{l}m=1 \\ m=-3\end{array}\right.$. Đối chiếu điều kiện ta được $m=1$ thỏa mãn yêu cầu bài toán.
Vậy $m=1$ là giá trị cần tìm.
Cho đường tròn $(O ; R)$ và đường thẳng $d$ không đi qua $O$ cắt $(O)$ tại hai điểm $A ; B$.
Trên tia đối của tia $BA$ lấy điểm $M$; qua $M$ kẻ hai tiếp tuyến $MC$; $MD$ với đường tròn $(O)$ ($C$; $D$ là các tiếp điểm). Gọi $H$ là trung điểm của $AB$.
a) Chứng minh tứ giác $OMCH$ nội tiếp.
b) $OM$ cắt đường tròn $(O)$ tại $I$ và cắt $CD$ tại $K$. Chứng minh $OK \cdot OM=R^{2}$
c) Đường thẳng qua $O$ vuông góc với $OM$, cắt tia $MC$ và $MD$ lần lượt tại $P$ và $Q$. Tính độ dài $OM$ theo $R$ sao cho diện tích tam giác $MPQ$ nhỏ nhất.
Hướng dẫn giải:
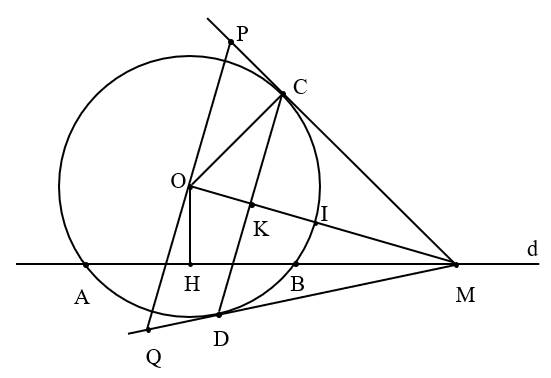
a) Vì $H$ là trung điểm của dây cung $AB$ nên $OH \perp AB \Rightarrow \widehat{OHM}=90^{\circ}$
Ta có: $\widehat{OHM}=\widehat{OCM}=90^{\circ}$ nên tứ giác $OMCH$ nội tiếp.
b) Tam giác $ODM$ vuông tại $D$ (vì $\widehat{O D M}=90^{\circ}$ ). Mặt khác: $MC=MD(t / c$ hai tiếp tuyến cắt nhau); $OC=OD=R \Rightarrow OM$ là đường trung trực của đoạn thẳng $CD \Rightarrow OM \perp CD$. Trong tam giác vuông $ODM$ áp dụng hệ thức lượng ta có: $OD^{2}=OK \cdot OM \Leftrightarrow OK \cdot OM=R^{2}$.
c) Theo tính chất hai tiếp tuyến cắt nhau ta có $MO$ là tia phân giác của góc $PMQ$, mặt khác $MO \perp PQ$ nên tam giác $PMQ$ cân tại $M \Rightarrow PQ=2 OP$.
Ta có $S_{\text {PMQ }}=\dfrac{1}{2} MO \cdot PQ=MO \cdot OP$. Trong tam giác vuông $OMQ$ ta có:
$$
\dfrac{1}{OD^{2}}=\dfrac{1}{OP^{2}}+\dfrac{1}{OM^{2}} \Leftrightarrow \dfrac{1}{R^{2}}=\dfrac{1}{OP^{2}}+\dfrac{1}{OM^{2}}
$$
Áp dụng bất đẳng thức AM-GM :
$$
\begin{aligned}
&\dfrac{1}{OP^{2}}+\dfrac{1}{OM^{2}} \geq 2 \sqrt{\dfrac{1}{OP^{2}} \cdot \dfrac{1}{OM^{2}}}=\dfrac{2}{OP \cdot OM} \Leftrightarrow \dfrac{1}{R^{2}} \geq \dfrac{2}{~S_{\text {PMP }}} \\
&S_{PMQ} \geq 2 R^{2} . \text { Dấu "=" xảy ra } \Leftrightarrow\left\{\begin{array}{l}
\dfrac{1}{OM}=\dfrac{1}{OP^{2}} \\
OM \cdot OP=2 R^{2}
\end{array} \Leftrightarrow OM=OP=R \sqrt{2} .\right.
\end{aligned}
$$
Vậy $S_{PMQ}$ đạt giá trị nhỏ nhất $\Leftrightarrow OM=R \sqrt{2}$.
