Nội dung đề thi (120 phút) SVIP

Hướng dẫn giải:

1. Với $x \geq 0$ và $x \neq 25$
$P=\dfrac{\sqrt{x}(\sqrt{x}-5)+2 \sqrt{x}(\sqrt{x}+5)-(3 x+25)}{(\sqrt{x}+5)(\sqrt{x}-5)}=\dfrac{x-5 \sqrt{x}+2 x+10 \sqrt{x}-3 x-25}{(\sqrt{x}+5)(\sqrt{x}-5)}$
$=\dfrac{5 \sqrt{x}-25}{(\sqrt{x}+5)(\sqrt{x}-5)}=\dfrac{5(\sqrt{x}-5)}{(\sqrt{x}+5)(\sqrt{x}-5)}=\dfrac{5}{\sqrt{x}+5}$ với $x \geq 0$ và $x \neq 25$. 
2. Để $P=\dfrac{5}{7}$ thì $\dfrac{5}{\sqrt{x}+5}=\dfrac{5}{7} \Leftrightarrow \sqrt{x}+5=7$ $\sqrt{x}=2 \Leftrightarrow x=4$ (thỏa mãn điều kiện)

Hướng dẫn giải:

Để đường thẳng $(d)$ đi qua điểm $A(1 ; 5)$ thì $x=1$ và $y=5$ thỏa mãn: $y=(2 m+1) x+m$. Khi đó: $5=(2 m+1) \cdot 1+m$ $\Leftrightarrow 3 m+1=5 \Leftrightarrow m=\dfrac{4}{3}$.

Vậy $m=\dfrac{4}{3}$ là giá trị cần tìm.

Hướng dẫn giải:

Ta có: 
$\left\{\begin{array}{l}4 x+3 y=11 \\ 4 x-y=7\end{array} \Leftrightarrow\left\{\begin{array}{l}4 x+3(4 x-7)=11 \\ y=4 x-7\end{array} \Leftrightarrow\left\{\begin{array}{l}16 x-21=11 \\ y=4 x-7\end{array}\right.\right.\right.$ $\left\{\begin{array}{l}x=2 \\ y=4 x-7\end{array} \Leftrightarrow\left\{\begin{array}{l}x=2 \\ y=1\end{array}\right.\right.$
Vậy $(x ; y)=(2 ; 1)$ là nghiệm duy nhất của hệ phương trình.

Hướng dẫn giải:

Các hệ số: $a=1 ; b=-6 ; c=5$.
Ta thấy $a+b+c=1+(-6)+5=0$
Nên phương trình có 2 nghiệm là: $x_{1}=1 ; x_{2}=\dfrac{c}{a}=\dfrac{5}{1}=5$.

Hướng dẫn giải:

Ta có: $\Delta^{\prime}=2-m$
Phương trình có 2 nghiệm $x_{1}$ và $x_{2}$ khi và chỉ khi $\Delta^{\prime} \geq 0 \Leftrightarrow m \leq 2$
Với $m \leq 2$, theo hệ thức Vi-ét ta có: $\left\{\begin{array}{l}x_{1}+x_{2}=2 \\ x_{1} \cdot x_{2}=m-1\end{array}\left(^{*}\right)\right.$
Ta có:
$$
\begin{aligned}
&x_{1}^{4}-x_{1}^{3}=x_{2}^{4}-x_{2}^{3} \Leftrightarrow x_{1}^{4}-x_{2}^{4}=x_{1}^{3}-x_{2}^{3} \Leftrightarrow\left(x_{1}-x_{2}\right)\left(x_{1}+x_{2}\right)\left(x_{1}^{2}+x_{2}^{2}\right)=\left(x_{1}-x_{2}\right)\left(x_{1}^{2}+x_{1} x_{2}+x_{2}^{2}\right) \\
&\Leftrightarrow\left(x_{1}-x_{2}\right)\left(x_{1}+x_{2}\right)\left[\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}\right]=\left(x_{1}-x_{2}\right)\left[\left(x_{1}+x_{2}\right)^{2}-x_{1} x_{2}\right]
\end{aligned}
$$
Thay các hệ thức (*) vào ta được:
$$
2\left(x_{1}-x_{2}\right)(6-2 m)=\left(x_{1}-x_{2}\right)(5-m) \Leftrightarrow\left(x_{1}-x_{2}\right)(7-3 m)=0
$$
1) Khi $x_{1}-x_{2}=0 \Leftrightarrow x_{1}=x_{2} \Leftrightarrow \Delta^{\prime}=0 \Leftrightarrow m=2$ (thỏa mãn)
2) $7-3 m=0 \Leftrightarrow m=\dfrac{7}{3}$ (loại)
Vậy $m=2$ là giá trị duy nhất cần tìm.

Hướng dẫn giải:

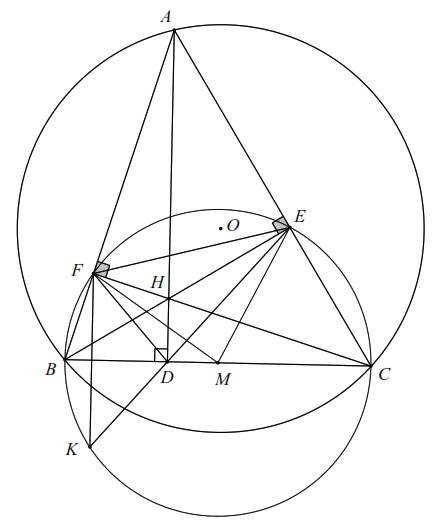
1. Do $B E, CF$ là đường cao của $\triangle A B C$ nên $B E \perp A C, CF \perp A B$
$\Rightarrow \widehat{A F H}=\widehat{A E H}=90^{\circ}$
Xét tứ giác $A E H F$ có: $\widehat{A F H}+\widehat{A E H}=90^{\circ}+90^{\circ}=180^{\circ}$ nên tứ giác $A E H F$ nội tiếp được đường tròn (đường kính $A H$ )
2. Gọi $I$ là trung điểm của $A H$.
Xét đường tròn $(O)$, có: $\widehat{F A D}=\widehat{F C D}$ (1) (Cùng phụ với góc $ABC$ )
Xét $\triangle A F H$ vuông tại $H$ có $F I$ là đường trung tuyến nên $F I=\dfrac{1}{2} A H \Rightarrow F I=A I$
Do đó $\triangle F I A$ cân tại $I$ nên $\widehat{I F A}=\widehat{I A F}$ (2)
Chứng minh tương tự được: $\triangle M F C$ cân tại $M$ nên $\widehat{M F C}=\widehat{M C F}$ (3)
Từ (1)(2)(3) $\Rightarrow \widehat{I F A}=\widehat{M F C}(4)$
Do $\widehat{A F I}+\widehat{I F C}=90^{\circ}(CF \perp A B)$ nên kết hợp với (4) ta được: $\widehat{M F C}+\widehat{I F C}=90^{\circ}$
Do đó $M F \perp F I$
Mà $F \in(I ; I A)$ là đường tròn ngoại tiếp tứ giác $AFHE, F I$ là bán kính $\Rightarrow M F$ là tiếp tuyến của $(I ; I A)$
Chứng minh tương tự với $M E$.
Vậy $M E, M F$ là các tiếp tuyến của đường tròn ngoại tiếp tứ giác $AF H E$

3. Gọi $K$ là điểm đối xứng với $F$ qua $B C \Rightarrow M F=M K$ (5)
Tứ giác $B F E C$ nội tiếp được đường tròn đường kính $B C$ (6)
Vì có $\widehat{C E B}=\widehat{B F C}=90^{\circ}$
Từ (4), (5) $\Rightarrow K \in(M ; M B)$
Xét đường tròn đi qua 5 điểm $B, E, F, C, K$, có: $\widehat{E B F}=\widehat{F K E}$ (hai góc nội tiếp chắn cung $\overparen{F E})(7)$
Tương tự:
Xét đường tròn ngoại tiếp tứ giác $A E D B$, có: $\widehat{E B A}=\widehat{E D A}$ (hai góc nội tiếp chắn cung $\overparen{E A})$ (8)
Từ (7), (8) $\Rightarrow \widehat{F K E}=\widehat{E D A}$
Kết hợp $F K / / A D$ (do cùng vuông góc với $B C$ ) $\Rightarrow K, D, E$ thẳng hàng
Do đó $D F+D E=D K+D E=K E$ (9)
Xét đường tròn $(M ; M B)$, khi đó: $K E \leq B C$ (10)
Vì vậy từ (9), (10) $\Rightarrow D E+D F \leq B C(đpcm)$.

Hướng dẫn giải:

Đặt $4 x-1=4 m ; 3 y-1=3 n ; 2 z-1=2 p$.
Khi đó $Q=24 m n p$
Ta có: $m, n, p>0$ và thỏa mãn $\dfrac{1}{m+1}+\dfrac{1}{n+1}+\dfrac{1}{p+1} \geq 2$
$\Leftrightarrow(m+1)(n+1)+(n+1)(p+1)+(p+1)(m+1) \geq 2(m+1)(n+1)(p+1)$
$\Leftrightarrow 1 \geq 2 m n p+m n+n p+p m$
Theo bất đẳng thức Cô-si cho ba số dương $mn, np, pm$.
Ta có: $1 \geq 2 m n p+m n+n p+p m \geq 2 m n p+3 \sqrt[3]{(m n p)^{2}}$
$\Rightarrow 1 \geq 2 m n p+3 \sqrt[3]{(m n p)^{2}}$ coi $\sqrt[3]{(m n p)^{2}}=t$ khi đó $Q=24 t^{3}$.
Ta có: $2 t^{3}+3 t^{2}-1 \leq 0 \Leftrightarrow(2 t-1)(t+1)^{2} \leq 0 \Rightarrow t \leq \dfrac{1}{2}$
Khi đó: $Q=24 m n p \leq 24 \cdot \dfrac{1}{8}=3 \Rightarrow \max{Q}=3$
Đạt được khi $m=n=p=\dfrac{1}{2} \Rightarrow x=\dfrac{3}{4} ; y=\dfrac{5}{6} ; z=1$.