Giao thoa sóng SVIP

I. Hiện tượng giao thoa của hai sóng mặt nước

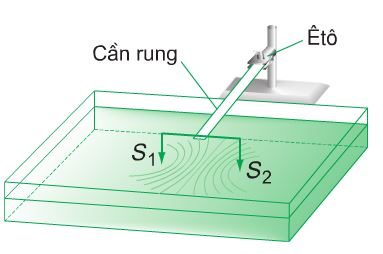
Khi gõ nhẹ cho cần rung dao động, ta thấy trên mặt nước xuất hiện một loạt gợn sóng ổn định có hình các đường hypebol và có tiêu điểm \(S_1,S_2\).

Giải thích:

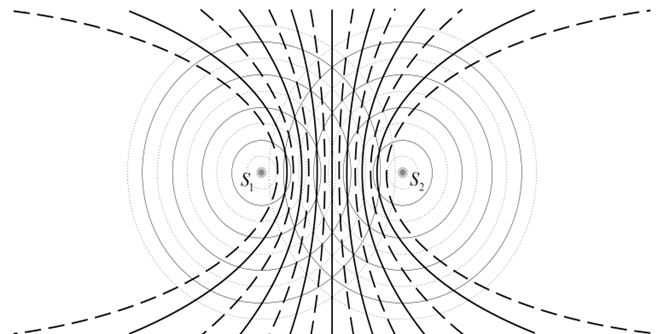
• Mỗi nguồn sóng phát ra một sóng có gợn sóng là những đường tròn. Những đường tròn nét liền miêu tả đỉnh sóng, còn nét đứt miêu tả hõm sóng.
• Ở trong miền hai sóng gặp nhau, có những điểm đứng yên, do hai sóng gặp nhau ở đó triệt tiêu nhau. Có những điểm dao động rất mạnh, do hai sóng gặp nhau ở đó tăng cường lẫn nhau. 
• Trong hình, những điểm đứng yên hợp thành những đường hypebol nét đứt, những điểm dao động mạnh hợp thành những đường hypebol nét liền.

Hiện tượng hai sóng gặp nhau tạo nên các gợn sóng ổn định gọi là hiện tượng giao thoa của hai sóng.

Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa.

II. Cực đại và cực tiểu

1. Dao động của một điểm trong vùng giao thoa

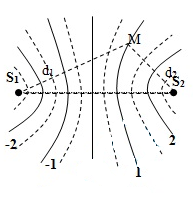
Gọi \(M\) là một điểm trong vùng giao thoa, lần lượt cách \(S_1\) và \(S_2\) những khoảng \(d_1\) và \(d_2\). 

Coi hai nguồn có cùng biên độ, cùng tần số, pha ban đầu bằng 0.

Phương trình dao động của hai nguồn là: 

\(u_{S_{ 1}}=u_{S_2}=A\cos\left(\omega t\right)\)

Phương trình dao động của phần tử tại \(M\) do hai nguồn gây ra lần lượt là:

\(u_{1M}=A\cos2\pi\left(\dfrac{t}{T}-\dfrac{d_1}{\lambda}\right)\)

\(u_{2M}=A\cos2\pi\left(\dfrac{t}{T}-\dfrac{d_2}{\lambda}\right)\)

Dao động của phần tử tại \(M\) là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số:

\(u_M=u_{1M}+u_{2M}=A\left[\cos2\pi\left(\dfrac{t}{T}-\dfrac{d_1}{\lambda}\right)+\cos2\pi\left(\dfrac{t}{T}-\dfrac{d_2}{\lambda}\right)\right]\)

\(u_M=2A\cos\dfrac{\pi\left(d_2-d_1\right)}{\lambda}\cos2\pi\left(\dfrac{t}{T}-\dfrac{d_1+d_2}{2\lambda}\right)\)

Biên độ dao động của phần tử tại \(M\) là

\(A_M=2A\left|\cos\dfrac{\pi\left(d_2-d_1\right)}{\lambda}\right|\)

2. Vị trí cực đại và cực tiểu

• Những điểm cực đại dao thoa là những điểm dao động với biên độ cực đại. Khi đó:

\(\left|\cos\dfrac{\pi\left(d_2-d_1\right)}{\lambda}\right|=1\Rightarrow\cos\dfrac{\pi\left(d_2-d_1\right)}{\lambda}=\pm1\)

\(\Rightarrow d_2-d_1=k\lambda\)

Những điểm dao động có biên độ cực đại là những điểm mà hiệu đường đi của hai sóng từ nguồn truyền tới bằng một số nguyên lần bước sóng \(\lambda\).

Nếu hai nguồn cùng pha, số điểm dao động cực đại giữa hai nguồn được tính theo công thức:

\(-\dfrac{l}{\lambda}< k< \dfrac{l}{\lambda}\)

Với \(l\) là khoảng cách giữa hai nguồn, \(k=0;\pm1;\pm2...\)

• Những điểm cực tiểu giao thoa là những điểm đứng yên. Khi đó

\(\cos\dfrac{\pi\left(d_2-d_1\right)}{\lambda}=0\)

\(\Rightarrow d_2-d_1=\left(k+\dfrac{1}{2}\right)\lambda\)

Những điểm tại đó dao động triệt tiêu là những điểm mà hiệu đường đi của hai sóng từ nguồn truyền tới bằng một nửa số nguyên lần bước sóng \(\lambda\).

Nếu hai nguồn cùng pha, số điểm dao động cực đại giữa hai nguồn được tính theo công thức:

\(-\dfrac{l}{\lambda}-\dfrac{1}{2}< k< \dfrac{l}{\lambda}-\dfrac{1}{2}\)

Với \(l\) là khoảng cách giữa hai nguồn, \(k=0;\pm1;\pm2...\)

III. Điều kiện giao thoa. Sóng kết hợp

Hai nguồn kết hợp là hai nguồn:

• dao động cùng phương, cùng tần số
• hiệu số pha không đổi theo thời gian

Hai sóng do hai nguồn kết hợp phát ra gọi là hai sóng kết hợp.

Để có các vân giao thoa trên mặt nước thì hai nguồn sóng phải là hai nguồn kết hợp.