Hai dạng toán cơ bản (tham khảo) SVIP

Dạng 1: Tìm giao tuyến của hai mặt phẳng (P) và (Q).

Bước 1: Tìm điểm chung thứ nhất.

Bước 2: Tìm hai đường thẳng đồng phẳng ở mỗi mặt phẳng, sau đó cho chúng cắt nhau, ta được điểm chung thứ hai.

Bước 3: Đường thẳng nối hai điểm chung của hai mặt phẳng là giao tuyến của mặt phẳng.

🔹 Ví dụ:

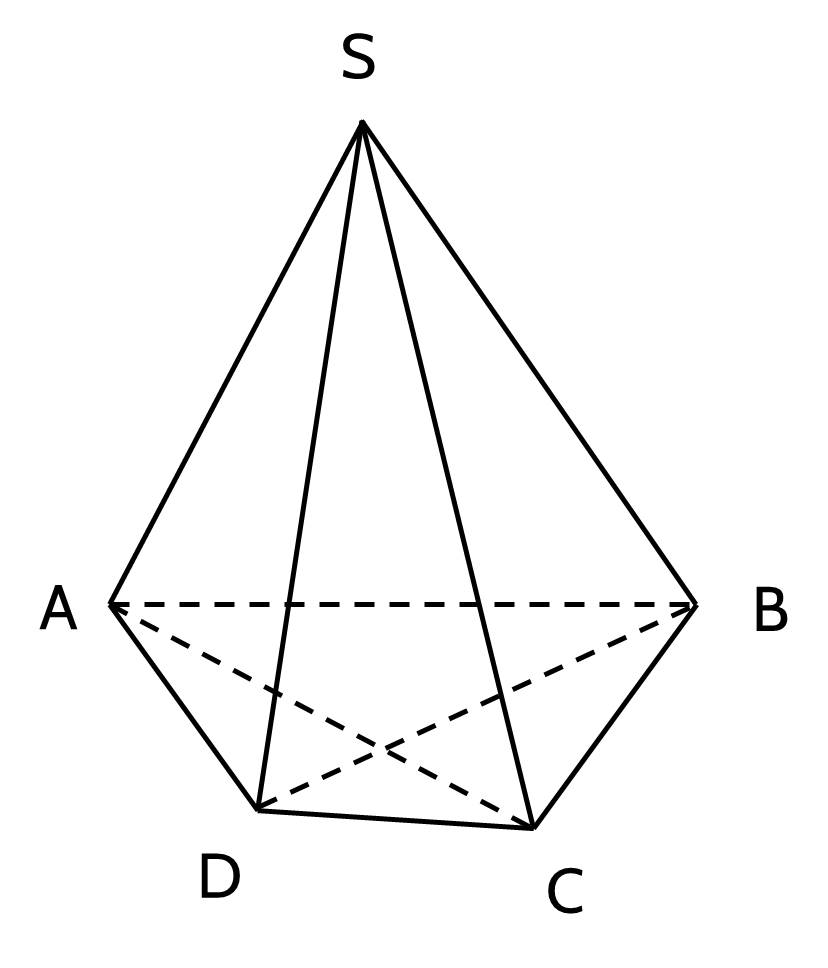
Cho hình chóp $S.ABCD$. Tìm giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$.

🔹 Hướng dẫn:

Bước 1: $S$ là điểm chung thứ nhất.

Bước 2: Hai đường thẳng cần tìm là $AC$ và $BD$ (cùng nằm trong mp đáy).

Bước 3: Gọi $O$ là giao điểm của $AC$ và $BD$. $O$ là điểm chung thứ hai của hai mặt phẳng, hay $SO$ là giao tuyến cần tìm.

🔹 Lời giải

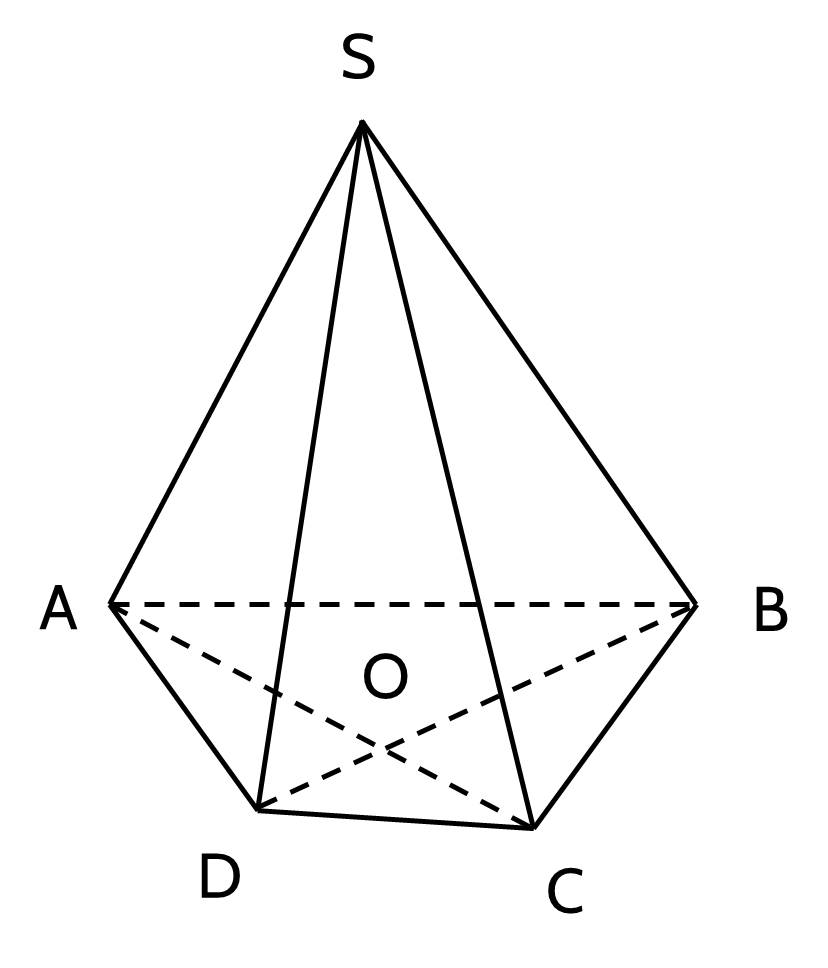
$S$ là điểm chung thứ nhất của hai mặt phẳng.

Trong mặt phẳng $(ABCD)$, $AC \cap BD = O$.

Vì $O\in AC$ mà $AC \subset (SAC)$ nên $O\in (SAC)$.

Vì $O\in BD$ mà $BD \subset (SBD)$ nên $O\in (SBD)$.

Vậy $O$ là điểm chung thứ hai của hai mặt phẳng, hay $SO$ là giao tuyến của hai mặt phẳng.

Dạng 2: Tìm giao điểm của đường thẳng d và mặt phẳng (P).

Bước 1: Chọn mặt phẳng (Q) thích hợp chứa đường thẳng d.

Bước 2: Tìm giao tuyến d' của hai mặt phẳng (P) và (Q).

Bước 3: Trong mặt phẳng (Q), cho d và d' cắt nhau tại I, I chính là giao điểm cần tìm.

🔹 Ví dụ:

Cho hình tứ diện $A B C D$ và $E$ là một điểm nằm trong tam giác $B C D$. Gọi $F$ là một điểm nằm giữa $A$ và $E$. Xác định giao điểm của đường thẳng $B F$ và mặt phẳng $(A C D)$.

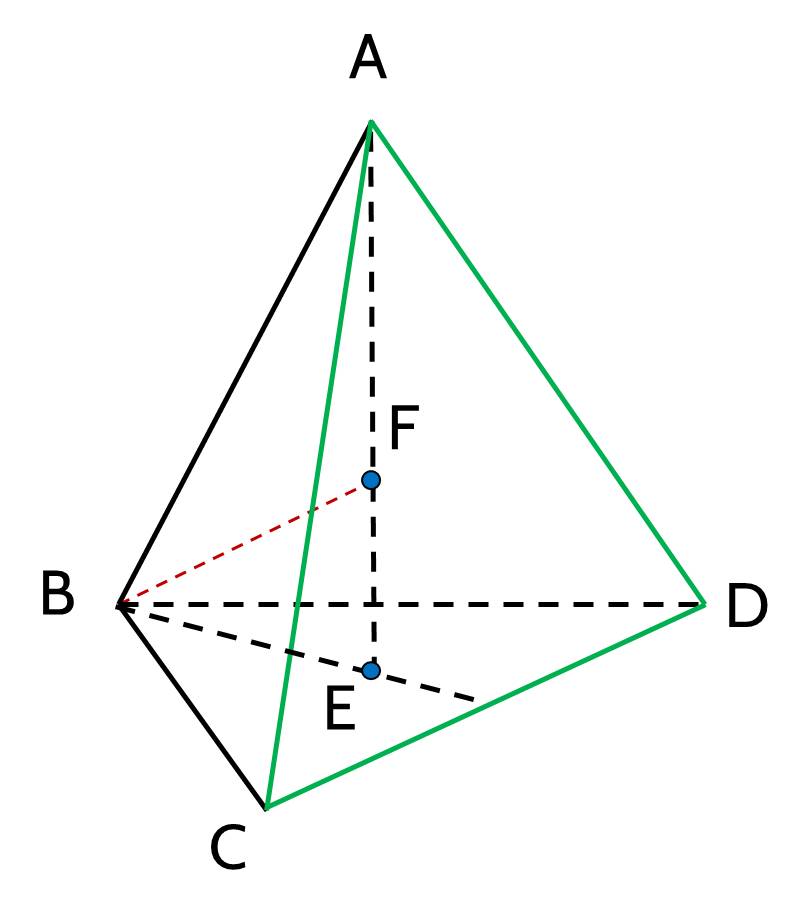
🔹 Hướng dẫn:

Bước 1: $BF$ nằm trong mặt phẳng $(ABE)$.

Bước 2: Tìm giao tuyến của mặt phẳng $(ABE)$ và $(ACD)$ (áp dụng các bước ở trên). 

Bước 3: Sau đó tìm giao điểm của BF và đường thẳng này.

🔹 Giải:

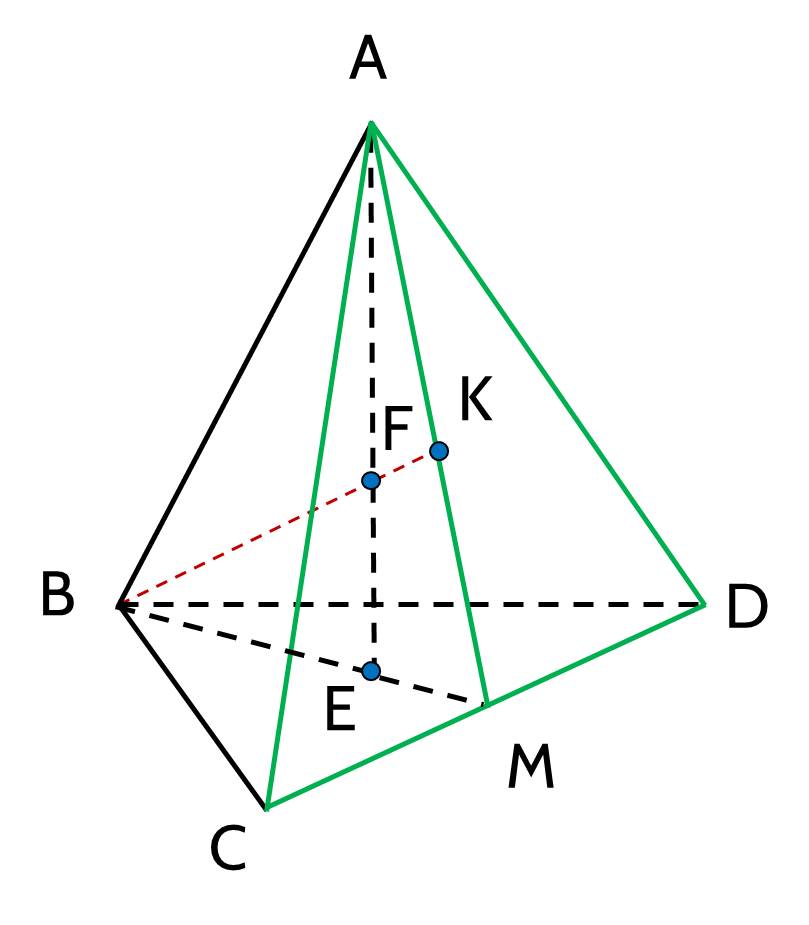
Vì điểm $E$ nằm trong tam giác $B C D$ nên đường thẳng $B E$ cắt cạnh $C D$ tại một điểm $M$. Các điểm $A, E$ thuộc mặt phẳng $(A B M)$ nên đường thẳng $A E$ thuộc mặt phẳng $(A B M)$, do đó điểm $F$ thuộc mặt phẳng $(A B M)$. Như vậy các điểm $A, B, E, F, M$ cùng thuộc mặt phẳng $(A B M)$.

Trong tam giác $A B M$, đường thẳng $B F$ cắt $A M$ tại $N$. Vì $N$ thuộc $A M$ và $A, M$ cùng thuộc mặt phẳng $(A C D)$ nên $N$ thuộc mặt phẳng $(A C D)$. Vậy $N$ là giao điểm của đường thẳng $B F$ và mặt phẳng $(A C D)$.