Lý thuyết SVIP

1. Định nghĩa

Tích vô hướng của hai vectơ có cùng điểm đầu

Cho hai vectơ \(\overrightarrow{OA}\), \(\overrightarrow{OB}\) khác \(\overrightarrow{0}\) trong mặt phẳng.

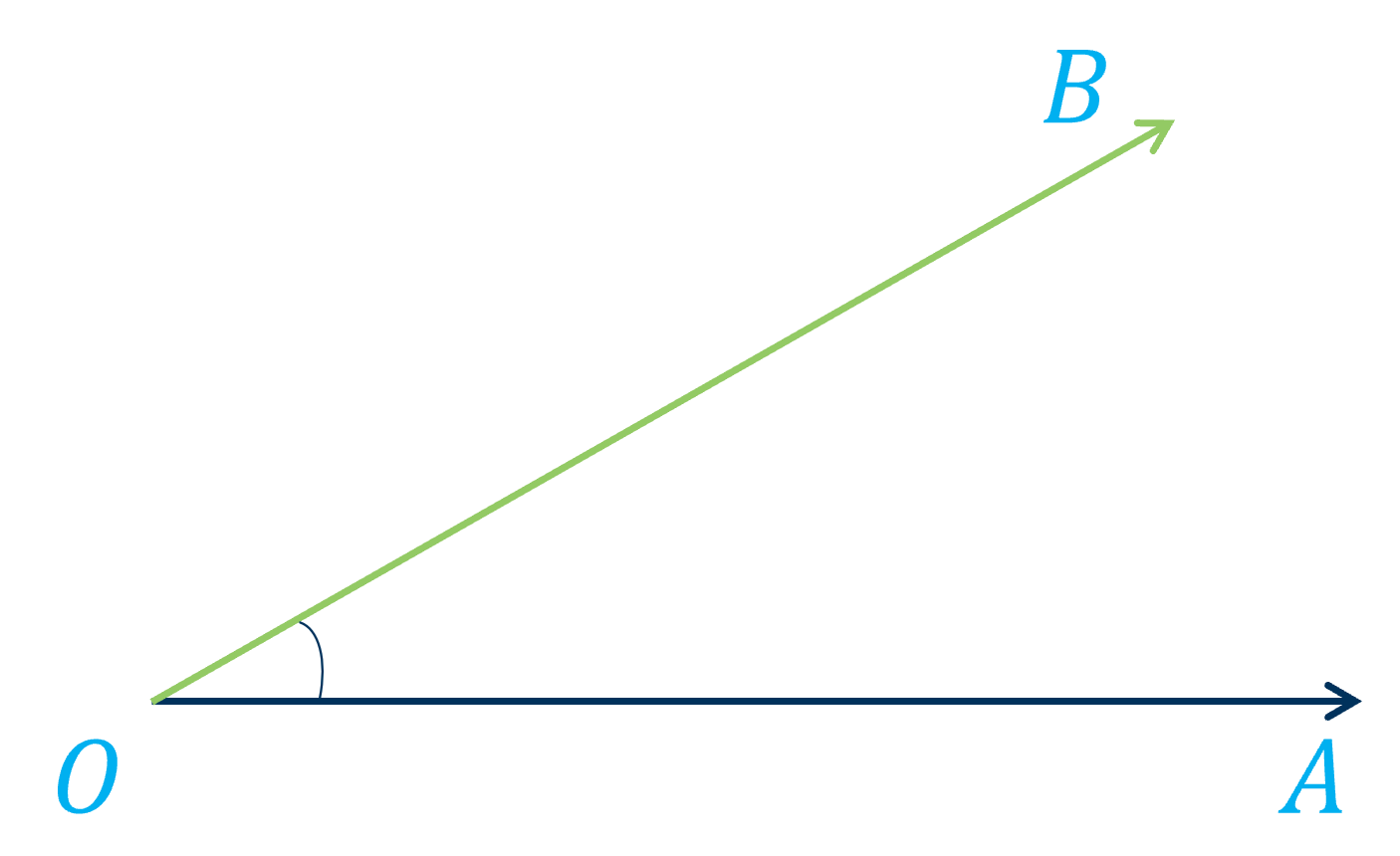
• Góc giữa hai vectơ \(\overrightarrow{OA}\), \(\overrightarrow{OB}\) là góc giữa hai tia \(OA\), \(OB\) và được kí hiệu là \(\left(\overrightarrow{OA},\overrightarrow{OB}\right)\).
• Tích vô hướng của hai vectơ \(\overrightarrow{OA}\) và \(\overrightarrow{OB}\) là một số, kí hiệu \(\overrightarrow{OA}.\overrightarrow{OB}\), được xác định bởi công thức: \(\overrightarrow{OA}.\overrightarrow{OB}=\left|\overrightarrow{OA}\right|.\left|\overrightarrow{OB}\right|.\cos\left(\overrightarrow{OA},\overrightarrow{OB}\right)\).

Tích vô hướng của hai vectơ tùy ý

Cho hai vectơ \(\overrightarrow{a}\), \(\overrightarrow{b}\) khác \(\overrightarrow{0}\). Lấy một điểm \(O\) và vẽ vectơ \(\overrightarrow{OA}=\overrightarrow{a}\), \(\overrightarrow{OB}=\overrightarrow{b}\). 

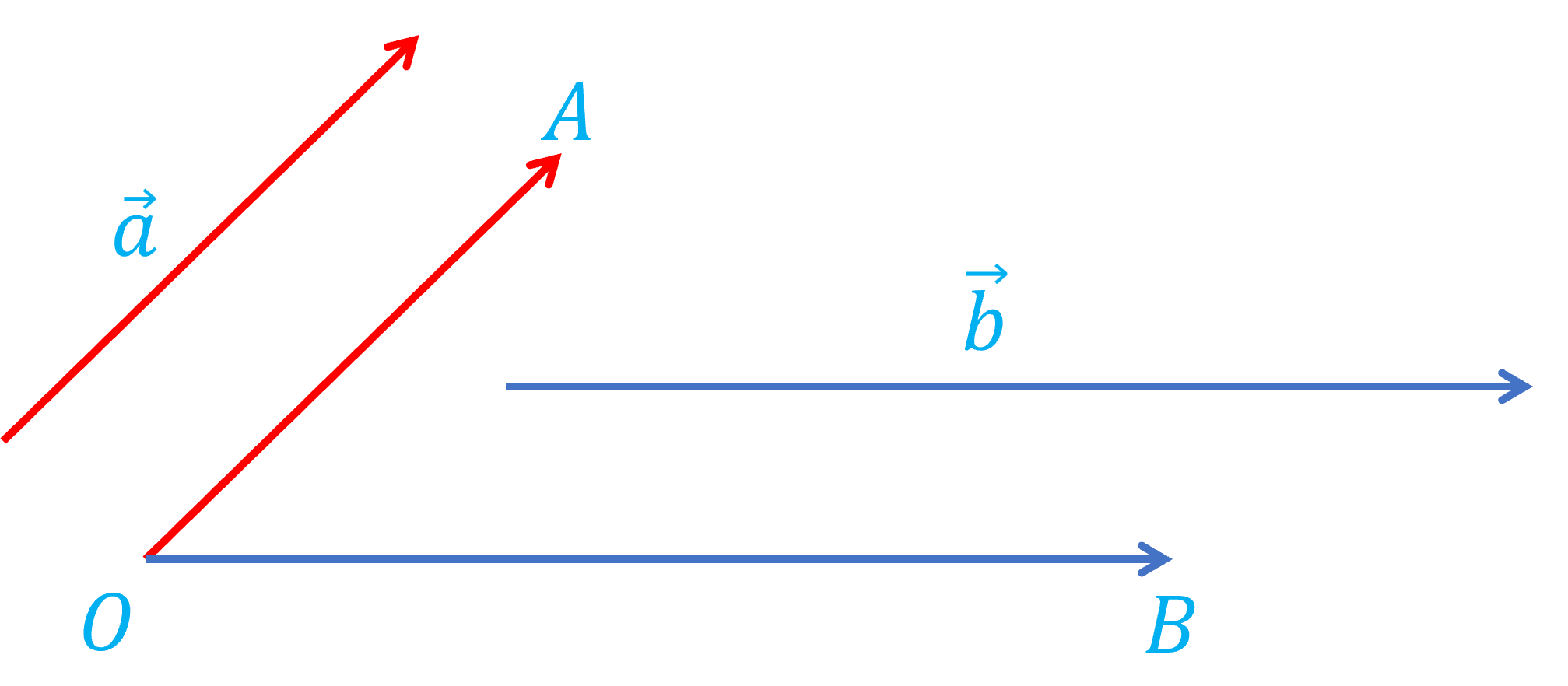
• Góc giữa hai vectơ \(\overrightarrow{a}\), \(\overrightarrow{b}\), kí hiệu \(\left(\overrightarrow{a},\overrightarrow{b}\right)\), là góc giữa hai vectơ \(\overrightarrow{OA}\), \(\overrightarrow{OB}\).
• Tích vô hướng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\), kí hiệu \(\overrightarrow{a}.\overrightarrow{b}\), là tích vô hướng của hai vectơ \(\overrightarrow{OA}\) và \(\overrightarrow{OB}\). Như vậy, tích vô hướng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là một số thực được xác định bởi công thức: \(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos\left(\overrightarrow{a},\overrightarrow{b}\right)\).

Quy ước: Tích vô hướng của một vectơ bất kì với vectơ \(\overrightarrow{0}\) là số \(0\).

Chú ý:

• \(\left(\overrightarrow{a},\overrightarrow{b}\right)=\left(\overrightarrow{b},\overrightarrow{a}\right)\);
• Nếu \(\left(\overrightarrow{a},\overrightarrow{b}\right)=90^o\) thì ta nói hai vectơ \(\overrightarrow{a}\), \(\overrightarrow{b}\) vuông góc với nhau, kí hiệu \(\overrightarrow{a}\perp\overrightarrow{b}\) hoặc \(\overrightarrow{b}\perp\overrightarrow{a}\). Khi đó \(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos90^o=0\);
• Khi \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng hướng thì \(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|\);
• Khi \(\overrightarrow{a}\) và \(\overrightarrow{b}\) ngược hướng thì \(\overrightarrow{a}.\overrightarrow{b}=-\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|\).

Ví dụ 1: Tính \(\overrightarrow{a}.\overrightarrow{b}\) trong các trường hợp sau: 

a) \(\left|\overrightarrow{a}\right|=6\), \(\left|\overrightarrow{b}\right|=7\), \(\left(\overrightarrow{a},\overrightarrow{b}\right)=45^o\); 

b) \(\left|\overrightarrow{a}\right|=8\), \(\left|\overrightarrow{b}\right|=9\), \(\left(\overrightarrow{a},\overrightarrow{b}\right)=150^o\).

Giải

a) \(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos\left(\overrightarrow{a},\overrightarrow{b}\right)=6.7.\cos45^o=42.\dfrac{\sqrt{2}}{2}=21\sqrt{2}\).

b) \(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos\left(\overrightarrow{a},\overrightarrow{b}\right)=8.9.\cos150^o=72.\dfrac{-\sqrt{3}}{2}=-36\sqrt{3}\).

2. Tính chất

Với hai vectơ bất kì \(\overrightarrow{a}\), \(\overrightarrow{b}\) và số thực \(k\) tùy ý, ta có: 

• \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}\) (tính chất giao hoán);
• \(\overrightarrow{a}\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}\) (tính chất phân phối);
• \(\left(k\overrightarrow{a}\right).\overrightarrow{b}=k\left(\overrightarrow{a}.\overrightarrow{b}\right)=\overrightarrow{a}.\left(k\overrightarrow{b}\right)\);
• \(\overrightarrow{a}^2\ge0,\overrightarrow{a}^2=0\Leftrightarrow\overrightarrow{a}=\overrightarrow{0}\).

Nhận xét: 

• \(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\overrightarrow{a}^2+2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\); \(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\);
• \(\left(\overrightarrow{a}-\overrightarrow{b}\right).\left(\overrightarrow{a}+\overrightarrow{b}\right)=\overrightarrow{a}^2-\overrightarrow{b}^2\).

Ví dụ 2: Cho hình bình hành \(ABCD\) có \(AB=3\), \(AD=4\), \(\widehat{A}=60^o\). \(M\) là trung điểm của \(CD\). Tính \(\overrightarrow{AM}.\overrightarrow{BD}\).

Giải

Ta có: \(\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{DC}=\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\), \(\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}\).

Suy ra 

\(\overrightarrow{AM}.\overrightarrow{BD}=\left(\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right).\left(\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{AD}^2+\dfrac{1}{2}\overrightarrow{AD}.\overrightarrow{AB}-\overrightarrow{AD}.\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AB}^2\)

\(=\overrightarrow{AD}^2-\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AD}-\dfrac{1}{2}\overrightarrow{AB}^2\)

\(=AD^2-\dfrac{1}{2}AD.AB.\cos\widehat{BAD}-\dfrac{1}{2}AB^2\)

\(=4^2-\dfrac{1}{2}.4.3.\cos60^o-\dfrac{1}{2}.3^2=\dfrac{17}{2}\).