Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) $(\sqrt{7}-\sqrt{5}) x-2=0 \Leftrightarrow(\sqrt{7}-\sqrt{5}) x=2 \Leftrightarrow x=\dfrac{2}{\sqrt{7}-\sqrt{5}} \Leftrightarrow x=\dfrac{2(\sqrt{7}+\sqrt{5})}{7-5} \Leftrightarrow x=\sqrt{7}+\sqrt{5}$
Vậy $x=\sqrt{7}+\sqrt{5}$ là nghiệm của phương trình.
b) Giải phương trình: $x^{2}+10 x-11=0(a=1 ; b=10 ; c=-11)$
Ta có: $a+b+c=1+10-11=0$ nên phương trình luôn có hai nghiệm
$
x=1 \text { và } x=\dfrac{c}{a}=-11
$
Vậy phương trình có tập nghiệm $S=\{1 ;-11\}$
c) Giải phương trình: $x^{4}-6 x^{2}+9=0$
Đặt $t=x^{2}$ với $t \geq 0$. Khi đó phương trình trở thành
$
t^{2}-6 t+9=0 \Leftrightarrow(t-3)^{2}=0 \Leftrightarrow t=3 \text { (thỏa mãn điều kiện) }
$
Với $t=3$ thì $x^{2}=3 \Leftrightarrow\left[\begin{array}{l}x=\sqrt{3} \\ x=-\sqrt{3}\end{array}\right.$
Vậy phương trình đã cho có tập nghiệm $S=\{\sqrt{3} ;-\sqrt{3}\}$

Hướng dẫn giải:

a) Xét phương trình hoành độ giao điểm: $a x^{2}=2 x \Leftrightarrow a x^{2}-2 x=0$ (1)
Do đồ thị hàm số $y=a x^{2}$ cắt đường thẳng $y=2 x$ tại điểm có hoành độ bằng 1 nên ta có $x=1$ là một nghiệm của phương trình (1).
Thay $x=1$ vào phương trình (1), ta có: $a-2=0 \Leftrightarrow a=2$.
Vậy $a=2$.

b) Đồ thị hàm số.

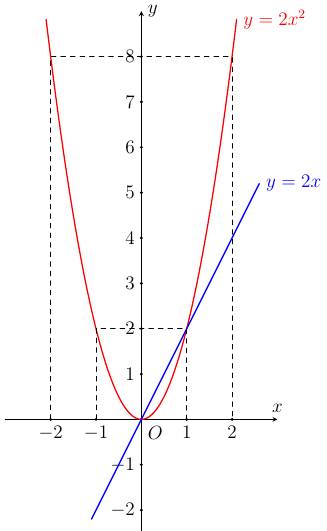
c) Dựa vào đồ thị trên, ta nhận thấy đồ thị hàm số $y=2 x^{2}$ cắt đồ thị hàm số $y=2 x$ tại hai điểm có hoành độ $x=0$ và $x=1$.
Vậy giao điểm thứ hai khác $A$ của hai đồ thi hàm số là $B(0,0)$.

Hướng dẫn giải:

Đổi 1 giờ 10 phút $=\dfrac{7}{6}(h), 1$ giờ 20 phút $=\dfrac{4}{3}(h)$.
Gọi vận tốc lên dốc và xuống dốc của người đó lần lượt là $x(km / h)$ và $y(km / h)$ với $y>x>0$
Lúc đi: Thời gian lên dốc là $\dfrac{5}{x}(h)$, xuống dốc là $\dfrac{10}{y}(h)$
Tổng thời gian đi hết 1 giờ 10 phút nên ta có phương trình: $\dfrac{5}{x}+\dfrac{10}{y}=\dfrac{7}{6}(1)$
Lúc về: Thời gian lên dốc là $\dfrac{10}{x}(h)$, xuống dốc là $\dfrac{5}{y}(h)$
Tổng thời gian đi hết 1 giờ 20 phút nên ta có phương trình: $\dfrac{10}{x}+\dfrac{5}{y}=\dfrac{4}{3}$ (2)
Từ (1) và (2), ta lập hệ phương trình: $\left\{\begin{array}{l}\dfrac{5}{x}+\dfrac{10}{y}=\dfrac{7}{6} \\ \dfrac{10}{x}+\dfrac{5}{y}=\dfrac{4}{3}\end{array}\right.$
Đặt $a=\dfrac{1}{x}$ và $b=\dfrac{1}{y}$ với $a>0, b>0$, ta được:
$
\left\{\begin{array} { l } 
{ 5 a + 1 0 b = \dfrac { 7 } { 6 } } \\
{ 1 0 a + 5 b = \dfrac { 4 } { 3 } }
\end{array} \Leftrightarrow \left\{\begin{array} { l } 
{ 1 0 a + 2 0 b = \dfrac { 7 } { 3 } } \\
{ 1 0 a + 5 b = \dfrac { 4 } { 3 } }
\end{array} \Leftrightarrow \left\{\begin{array} { l } 
{ 1 0 a + 5 b = \dfrac { 4 } { 3 } } \\
{ 1 5 b = 1 }
\end{array} \Leftrightarrow \left\{\begin{array} { l } 
{ 1 0 a + 5 \cdot \dfrac { 1 } { 1 5 } = \dfrac { 4 } { 3 } } \\
{ b = \dfrac { 1 } { 1 5 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
a=\dfrac{1}{10} \\
b=\dfrac{1}{15}
\end{array}\right.\right.\right.\right.\right. \text { (Nhận) }
$
Từ đây ta suy ra
$
\left\{\begin{array} { l } 
{ \dfrac { 1 } { x } = \dfrac { 1 } { 1 0 } } \\
{ \dfrac { 1 } { y } = \dfrac { 1 } { 1 5 } }
\end{array} \Rightarrow \left\{\begin{array}{l}
x=10 \\
y=15
\end{array}\right.\right. \text { (Nhận) }
$
Vậy vận tốc lúc lên dốc là $10(km / h)$ và vận tốc xuống dốc là $15(km / h)$.

Hướng dẫn giải:

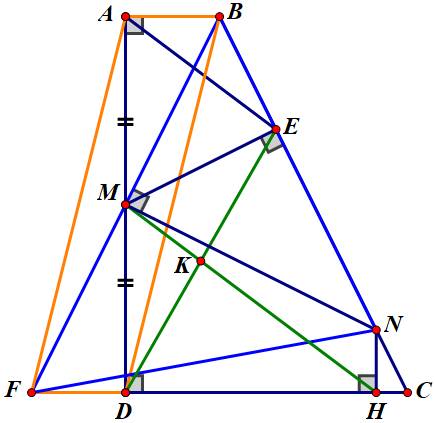
a) Chứng minh rằng $\widehat{M A E}=\widehat{M B E}$.
Xét tứ giác $A B E M$ có
$\widehat{M A B}=90^{\circ}$ (gt) và $\widehat{M E B}=90^{\circ}(E$ là hình chiếu vuông góc của $M$ lên $B C$ )
$\Rightarrow \widehat{M A B}+\widehat{M E B}=90^{\circ}+90^{\circ}=180^{\circ}$
$\Rightarrow$ Tứ giác $A B E M$ nội tiếp (tứ giác có tổng hai góc đối trong bù nhau)
$\Rightarrow \widehat{M A E}=\widehat{M B E}$ (hai góc nội tiếp cùng chắn cung $M E$ ).
b) Chứng minh rằng $A B D F$ là hình bình hành.
Ta có: $A B / / C D(A B C D$ là hình thang $) \Rightarrow A B / / D F$
Áp dụng hệ quả của định lý Ta-let, ta có: $\dfrac{A B}{D F}=\dfrac{A M}{M D}$
Mà $A M=M D(M$ là trung điểm $A D)$ nên $\dfrac{A B}{D F}=1 \Rightarrow A B=D F$
Xét tứ giác $A B D F$, ta có: $A B / / D F$ (cmt) và $A B=D F$ (cmt)
$\Rightarrow$ Tứ giác $A B D F$ là hình binh hành (tứ giác có một cặp cạnh vừa song song vừa bằng nhau).
c) Chứng minh rằng tam giác BNF cân.
Ta có: $A B D F$ là hình bình hành (cmt)
$\Rightarrow$ Hai đường chéo $A D$ và $B F$ cắt nhau tại trung điểm của mỗi đường
Mà $M$ là trung điểm $A D$ ( $gt$ ) nên $M$ cũng là trung điểm $B F$.
Xét $\triangle B N F$ có:
$N M$ là đường trung tuyến $(M$ là trung điểm $B F)$ và $N M$ là đường cao $(M N \perp B F)$
$\Rightarrow \Delta B N F$ cân tại $N$ (tam giác có trung tuyến đồng thời là đường cao)
d) Chíng minh rằng đurờng thẳng $M H$ đi qua trung điểm của $D E$.
Gọi $K$ là giao điểm của $M H$ và $D E$.
Xét tứ giác $M N H F$ có
$\widehat{F M N}=90^{\circ}(M N \perp B F)$ và $\widehat{N H F}=90^{\circ}$ ( $H$ là hình chiếu vuông góc của $N$ lên $\left.C D\right)$ $\Rightarrow \widehat{F M N}+\widehat{N H F}=90^{\circ}+90^{\circ}=180^{\circ}$
$\Rightarrow$ Tứ giác $M N H F$ nội tiếp (tứ giác có tổng hai góc đối trong bù nhau)
$\Rightarrow \widehat{H F N}=\widehat{H M N}$ (hai góc nội tiếp cùng chắn cung $H N$ )
Ta có: $\widehat{N F M}=\widehat{N B M}(\triangle N B F$ cân tại $N)$ mà $\widehat{N B M}=\widehat{N M E}$ (cùng phụ $\widehat{B M E}$ ) $\Rightarrow \widehat{N F M}=\widehat{N M E}$
(2)
Từ (1) và (2), ta cộng vế theo vế, ta được: $\widehat{H M N}+\widehat{N M E}=\widehat{H F N}+\widehat{N F M} \Rightarrow \widehat{H M E}=\widehat{H F M}$
Mà $\widehat{H F M}=\widehat{A B M}$ (so le trong của $A B / / D F$ )
Mặt khác, $\widehat{A B M}=\widehat{A E M}$ (hai góc nội tiếp cùng chắn $\widehat{A M}, A B E M$ nội tiếp)
$\Rightarrow \widehat{H M E}=\widehat{A E M}$ mà hai góc nằm ở vị trí so le trong nên $A E / / M H$
Xét $\triangle A E D$ có: $M$ là trung điểm $A D(gt)$ và $A E / / M K(K \in M H, A E / / M H)$
$\Rightarrow K$ là trung điểm $D E$ (định ly đường trung bình trong tam giác)
Vậy $M H$ luôn đi qua trung điểm của $D E$ (đpcm).