Phân tích một số ra thừa số nguyên tố SVIP

I. CÁCH TÌM MỘT ƯỚC NGUYÊN TỐ CỦA MỘT SỐ

Để tìm một ước nguyên tố của số tự nhiên lớn hơn $1$, ta có thể làm như sau:

⚡ Lần lượt thực hiện phép chia  cho các số nguyên tố theo thứ tự tăng dần $2,\, 3,\, 5,\, 7,\, 11,\, 13,\, ...$

⚡ Khi đó, phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của .

Ví dụ 1: Tìm một ước nguyên tố của $217$.

Giải

Theo dấu hiệu chia hết, số $217$ không chia hết cho các số nguyên tố $2,\,3,\,5$.

Ta có $217=7.31$. Vì thế $7$ là một ước nguyên tố của $217$.

II. PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ

Phân tích một số tự nhiên lớn hơn $1$ ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Ví dụ 2: 

- Phân tích $8$ ra thừa số nguyên tố được kết quả là $8=2^3$.

- Phân tích $15$ ra thừa số nguyên tố được kết quả là $15=3.5$.

​ PHƯƠNG PHÁP PHÂN TÍCH THEO SƠ ĐỒ HÌNH CÂY (RẼ NHÁNH)

Ví dụ 3: Viết số $12$ thành tích của các thừa số nguyên tố.

- Tìm một ước nguyên tố của $12$, chẳng hạn là $2$.

- Viết số $12$ thành tích của $2$ với một thừa số khác: $12=2.6$

​  

- Tiếp tục tìm một ước nguyên tố của $6$, chẳng hạn là $2$.

- Viết số $6$ thành tích của $2$ với một thừa số khác: $6=2.3$ .

​ 

- Các thừa số $2$ và $3$ đều là số nguyên tố nên ta dừng lại.

- Lấy tích tất cả các thừa số ở cuối cùng mỗi nhánh ta có: $12=2.2.3=2^2.3$ .

 PHƯƠNG PHÁP PHÂN TÍCH THEO SƠ ĐỒ CỘT

Ví dụ 4: Phân tích $12$ thành tích các thừa số nguyên tố theo cột dọc

 Vậy $12=2.2.3=2^2.3$

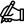  Lưu ý: 

Ta nên chia mỗi số cho ước nguyên tố nhỏ nhất của nó.

Cứ tiếp tục chia như thế cho đến khi được thương là $1$. 

Ví dụ 5: Phân tích số $72$ ra thừa số nguyên tố bằng $2$ cách.​

Cách 1: Sơ đồ cây                                                     Cách 2: Sơ đồ cột

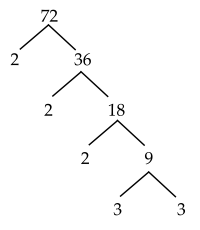
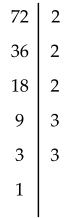
Vậy ta có phân tích $72=2.2.2.3.3=2^3.3^2$

Chú ý: 

- Thông thường, khi phân tích một số tự nhiên ra thừa số nguyên tố, các ước nguyên tố được viết theo thứ tự tăng dần.

- Ngoài cách làm như trên, ta cũng có thể phân tích một số ra thừa số nguyên tố bằng cách viết số đó thành tích của hai thừa số một cách linh hoạt.

Ví dụ 6: Phân tích số $120$ ra thừa số nguyên tố.

Giải

Cách 1: 

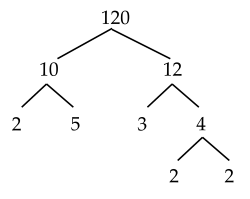
Vậy $120=2.5.3.2.2=2^3.3.5$

Cách 2: 

​ 

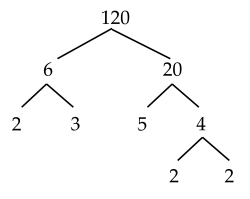
Vậy $120=2.3.5.2.2=2^3.3.5$.

Nhận xét: Dù phân tích một số ra thừa số nguyên tố bằng cách nào thì cuối cùng ta cũng được cùng một kết quả.