Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận SVIP
(1 điểm) So sánh
a) $\dfrac{-3}{8}$ và $\dfrac{5}{-12}$.
b) $\dfrac{3131}{5252}$ và $\dfrac{31}{52}$.
Hướng dẫn giải:
a) Có $\dfrac{-3}{8}=\dfrac{-9}{24} ; \dfrac{5}{-12}=\dfrac{-10}{12}$
Vì $\dfrac{-9}{24}>\dfrac{-10}{24}$ nên $\dfrac{-3}{8}>\dfrac{5}{-12}$.
b) Có $\dfrac{3131}{5252}=\dfrac{3131: 101}{5252: 101}=\dfrac{31}{52}$.
Vậy $\dfrac{3131}{5252}=\dfrac{31}{52}$.
Thực hiện các phép tính sau:
a) $\dfrac{-5}{9}+\dfrac{8}{15}+\dfrac{-2}{11}+\dfrac{4}{-9}+\dfrac{7}{15}$.
b) $\left(\dfrac{7}{2} . \dfrac{5}{6}\right)+\left(\dfrac{7}{6}: \dfrac{2}{7}\right)$.
Hướng dẫn giải:
a) $\dfrac{-5}{9}+\dfrac{8}{15}+\dfrac{-2}{11}+\dfrac{4}{-9}+\dfrac{7}{15}= \left(\dfrac{-5}{9}+\dfrac{-4}{9}\right)+\left(\dfrac{8}{15}+\dfrac{7}{15}\right)+\dfrac{-2}{11}$
$=\dfrac{-9}{9}+\dfrac{15}{15}+\dfrac{-2}{11}$
$=-1+1+\dfrac{-2}{11}$
$=0+\dfrac{-2}{11}=\dfrac{-2}{11}$.
b) $\left(\dfrac{7}{2} . \dfrac{5}{6}\right)+\left(\dfrac{7}{6}: \dfrac{2}{7}\right)$
$=\left(\dfrac{7}{2} . \dfrac{5}{6}\right)+\left(\dfrac{7}{6} . \dfrac{7}{2}\right)$
$=\dfrac{7}{2} .\left(\dfrac{5}{6}+\dfrac{7}{6}\right)$
$=\dfrac{7}{2} . 2$
$=7$
(1,0 điểm) Một đám đất hình chữ nhật có chiều rộng $60$ m, chiều dài bằng $\dfrac{4}{3}$ chiều rộng. Người ta để $\dfrac{7}{12}$ diện tích đám đất đó trồng cây, $30 \%$ diện tích còn lại đó để đào ao thả cá. Hãy tính diện tích ao thả cá?
Hướng dẫn giải:
Chiều dài đám đất là:
$60 . \dfrac{4}{3}=80$ (m)
Diện tích đám đất là:
$60.80=4\,800$ (m$^2$)
Diện tích trồng cây là:
$4\,800 . \dfrac{7}{12}=2\,800$ (m$^2$)
Diện tích còn lại là:
$4\,800-2\,800=2\,000$ (m$^2$)
Diện tích ao cá:
$2\,000.30 \%=600$ (m$^2$)
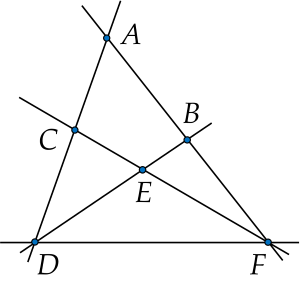
1. Cho hình vẽ sau. Kể tên các bộ 3 điểm thẳng hàng.
2. Vẽ đoạn thẳng ${AB}=9$ cm. Điểm $ {I}$ nằm giữa $ {A}$ và $ {B}$ sao cho $ {AI}=4$ cm.
a) Tính độ dài đoạn thẳng $ {IB}$.
b) Gọi $ {E}$ là trung điểm đoạn thẳng $ {IB}$. Tính độ dài đoạn thẳng $ {AE}$.
Hướng dẫn giải:
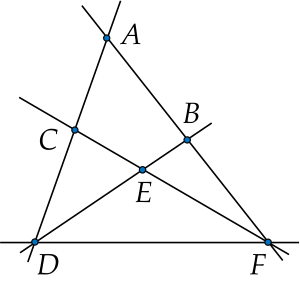
1. Trong hình vẽ có 4 bộ ba điểm thẳng là:
+) ${A}, {C}, {D}$
+) $A, B, E$
+) $C, E, F$
+) $D, E, B$
2.
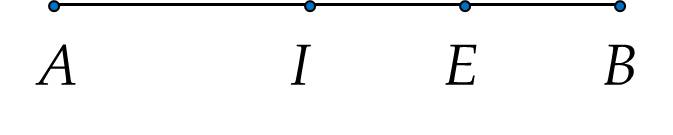
a) Theo hình vẽ, ta có: $A I+I B=A B$
Hay $4+{IB}=9$
${IB}=9-4=5$ cm
b) Vì ${E}$ là trung điểm của ${IB}$ nên
$E I=E B=\dfrac{I B}{2}=\dfrac{5}{2}=2,5$ (cm)
Theo hình vẽ, ta có: ${AE}={AI}+{IE}=4+2,5=6,5$ (cm)
Chứng minh $M=\dfrac{n-1}{n-2} (n \in \mathbb Z;n \neq 2)$ là phân số tối giản.
Hướng dẫn giải:
Để chứng minh phân số tối giản, ta chứng minh ƯCLN của tử số và mẫu số là $1$.
Goi ƯCLN $(n-1 ; n-2)=d \Rightarrow n-1: d$ và $n-2: d$
$\Rightarrow(n-1)-(n-2): d \Rightarrow 1: d$
$\Rightarrow d=1$ với mọi $n$.
Vậy với mọi $n \in \mathbb Z$ thì $M=\dfrac{n-1}{n-2}$ là phân số tối giản.
