Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (6 điểm) SVIP
(2 điểm)
a. Cho một dòng điện \(I\) chạy trong một dây dẫn thẳng dài vô hạn. Biểu diễn đường sức từ do dòng điện \(I\) gây ra và đi qua điểm M và N trên hình vẽ. Xác định phương, chiều của vectơ cảm ứng từ tại điểm M và điểm N.
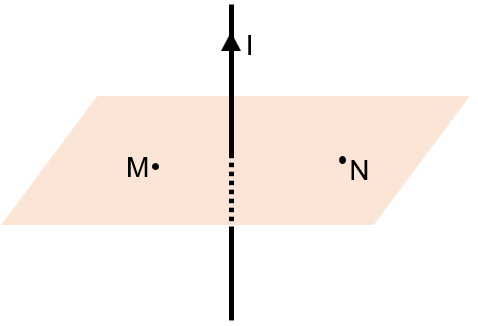
b. Cho dòng điện \(I=2\) A. Tính độ lớn vectơ cảm ứng từ tại M và N biết \(r_M=6\) cm và \(r_N=8\) cm.
Hướng dẫn giải:
a. Đường sức từ gây bởi một dòng điện thẳng dài là những đường tròn nằm trong mặt phẳng vuông góc với dòng điện và có tâm nằm trên dòng điện. Từ đó ta vẽ được các đường sức từ đi qua M và N.
Áp dụng quy tắc nắm tay phải, xác định được chiều các đường sức từ đi qua M và N.
Từ đó xác định được chiều của vectơ cảm ứng từ tại M và N.
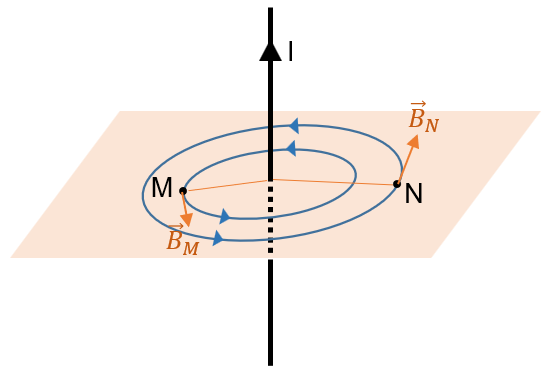
b. \(B_M=2.10^{-7}.\dfrac{I}{r_M}=2.10^{-7}.\dfrac{2}{0,06}=6,6.10^{-6}T\)
\(B_N=2.10^{-7}.\dfrac{I}{r_N}=2.10^{-7}.\dfrac{2}{0,08}=5.10^{-6}T\)
(2 điểm)
Một vòng dây phẳng có diện tích 80 cm2 đặt trong từ trường đều B = 0,3.10-3 T. Ban đầu vectơ cảm ứng từ vuông góc với mặt phẳng vòng dây. Đột ngột vectơ cảm ứng từ đổi hướng song song với mặt phẳng vòng dây trong 10-3 s.
a. Tính độ biến thiên từ thông qua mặt phẳng vòng dây.
b. Trong thời gian đổi hướng, suất điện động cảm ứng xuất hiện trong khung là bao nhiêu?
Hướng dẫn giải:
\(S=80cm^2=80.\left(10^{-2}\right)^2=8.10^{-3}m^2\)
a. Từ thông ban đầu qua mặt phẳng vòng dây:
\(\phi_1=BS\cos\left(\vec{n};\vec{B}\right)=BS\cos0^0=BS\)
Từ thông lúc sau qua mặt phẳng vòng dây:
\(\phi_2=BS\cos\left(\vec{n};\vec{B}\right)=BS\cos180^0=-BS\)
Độ biến thiên từ thông qua mặt phẳng vòng dây là:
\(\Delta\phi=\phi_2-\phi_1=-BS-BS=-2BS=-2.0,3.10^{-3}.8.10^{-3}=-4,8.10^{-6}\left(Wb\right)\)
b. Suất điện động cảm ứng:
\(\left|e_c\right|=\left|\dfrac{\Delta\phi}{\Delta t}\right|=\left|-\dfrac{2NBS}{\Delta t}\right|=\left|-\dfrac{4,8.10^{-6}}{10^{-3}}\right|=4,8.10^{-3}\left(V\right)\)
(2 điểm)
Một ống dây dài \(l=30\) cm gồm \(N=1000\) vòng dây, đường kính mỗi vòng dây \(d=6\) cm có dòng điện với cường độ \(i=2\) A đi qua.
a) Tính độ tự cảm của ống dây.
b) Tính từ thông qua mỗi vòng dây.
c) Thời gian ngắt dòng điện là \(t=0,1\) giây, tính suất điện động tự cảm xuất hiện trong ống dây.
Hướng dẫn giải:
a. Độ tự cảm của ống dây:
\(L=4\pi.10^{-7}\mu\dfrac{N^2}{l}S=4\pi.10^{-7}\mu\dfrac{N^2}{l}.\dfrac{\pi d^2}{4}\)\(=4\pi.10^{-7}.\dfrac{1000^2}{0,3}.\dfrac{0,06^2}{4}.\pi=0,012\) H
b. Từ thông qua ống dây: \(\phi=Li=0,012.2=0,024\) Wb
Từ thông qua mỗi vòng dây: \(\phi_1=\dfrac{\phi}{N}=\dfrac{0,024}{1000}=0,0024\) Wb
c. Suất điện động tự cảm xuất hiện trong ống dây:
\(\left|e_{tc}\right|=\left|L.\dfrac{\Delta i}{\Delta t}\right|=\left|0,012.\dfrac{0-2}{0,1}\right|=0,24\) V
