Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Bài 1:
a) (0,75 điểm) Viết các số sau bằng số La Mã: 6; 24; 39.
b) (0,5 điểm) Viết các ước lớn hơn 6 của số 36.
Hướng dẫn giải:
a) 6 = VI; 24 = XXIV; 39 = XXXIX.
b) Các ước lớn hơn 6 của số 36 là: 9; 12; 18; 36.
Bài 2. (1 điểm) Thực hiện phép tính:
a) $67. 36 + 67. 65 - 67$;
b) $(7^{23}. 45 + 7^{23}. 4) \, : \, 7^{25}$.
Hướng dẫn giải:
a) $67. 36 + 67. 65 - 67$
$= 67. (36 + 65 - 1)$
$= 67. 100 = 6$ $700$
b) $(7^{23}. 45 + 7^{23}. 4) \, : \, 7^{25}$
$= 7^{23}.(45 + 4) \, : \, 7^{25}$
$ = 7^{23}. 49 \, : \, 7^{25}$
$ = 7^{23}. 7^2 \, : \, 7^{25}$
$ = 7^{25} \, : \, 7^{25} = 1$.
Bài 3. (1 điểm) Mẹ Lan mang $160$ $000$ đồng vào siêu thị mua $2$ kg khoai tây và $5$ kg gạo .Giá mỗi ki-lô-gam khoai tây là $24$ $500$ đồng, mỗi ki-lô-gam gạo là $21$ $000$ đồng. Hỏi mẹ Lan còn lại bao nhiêu tiền?
Hướng dẫn giải:
Số tiền mà mẹ Lan đã mua là:
$24$ $500$ . $2$ + $21$ $000$ . $5 = 154$ $000$ (đồng)
Số tiền còn lại của Mẹ Lan sau khi mua là:
$160$ $000 - 154$ $000 = 6$ $000$ (đồng).
Bài 4 (1,25 điểm)
a) Cho hình vuông $ABCD$, có $AB=4$ cm.
Tính độ dài các đoạn thẳng $BC$, $CD$, $AD$.
Cho biết số đo các góc đỉnh $A$; $B$; $C$; $D$.
b) Dùng thước thẳng và compa, vẽ tam giác đều $ABC$ có cạnh $AC$ bằng $4$ cm.
Hướng dẫn giải:
a) Hình vuông có bốn cạnh bằng nhau: $AB=BC=CD=DA=4$ cm
Và bốn góc đỉnh $A$, $B$, $C$, $D$ bằng nhau và đều là góc vuông (góc $90^\circ$).
b) Gợi ý:
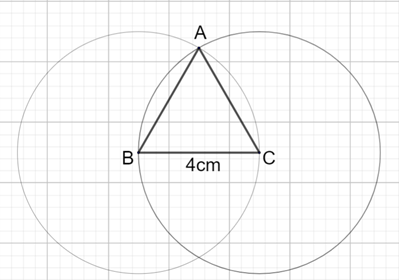
Bài 5 (1,5 điểm)
a) Quan sát hình vẽ.
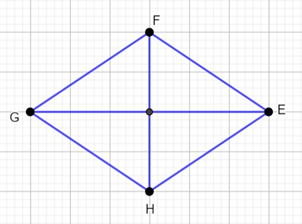
Em hãy mô tả về cạnh, cạnh đối diện và đường chéo của hình thoi $EFGH.$
b) Dùng thước thẳng và compa, vẽ hình bình hành $ABCD$ có cạnh $AB$ bằng $3$ cm và cạnh $BC$ bằng $8$ cm.
Hướng dẫn giải:
a)
Bốn cạnh bằng nhau: EF = FG = GH = HE;
Hai cặp cạnh đối EF và GH, GF và EH song song với nhau;
Bốn đỉnh E, F, G, H.
Hai đường chéo EG, HF vuông góc với nhau.
b) Học sinh tự vẽ hình.
Bài 6 (0,5 điểm) Tại một bến xe cứ $10$ phút lại có một chuyến taxi rời bến, cứ $12$ phút lại có xe buýt rời bến. Lúc 6 giờ, một chuyến xe taxi và một xe buýt cùng rời bến một lúc. Hỏi lúc mấy giờ lại có một xe taxi và xe buýt cùng rời bến lần tiếp theo?
Hướng dẫn giải:
Gọi $x$ là số phút ít nhất để một chuyến xe taxi và một xe buýt cùng rời bến một lúc.
Theo đề bài, ta có: $x \, \vdots \, 10$; $x \, \vdots \, 12$ và $x$ nhỏ nhất có thể.
Nên $x$ là BCNN$(10,12)$.
Mà $10 = 2.5$; $12 = 22.3$
Suy ra BCNN$(10,12)= 22.3.5=60$ hay $x=60$.
Vậy sau $60$ phút hay $1$ giờ nữa, tức là vào lúc 7 giờ một chuyến xe taxi và một xe buýt sẽ lại cùng rời bến một lúc.
Bài 7 (0,5 điểm) Quan sát hình bên dưới.
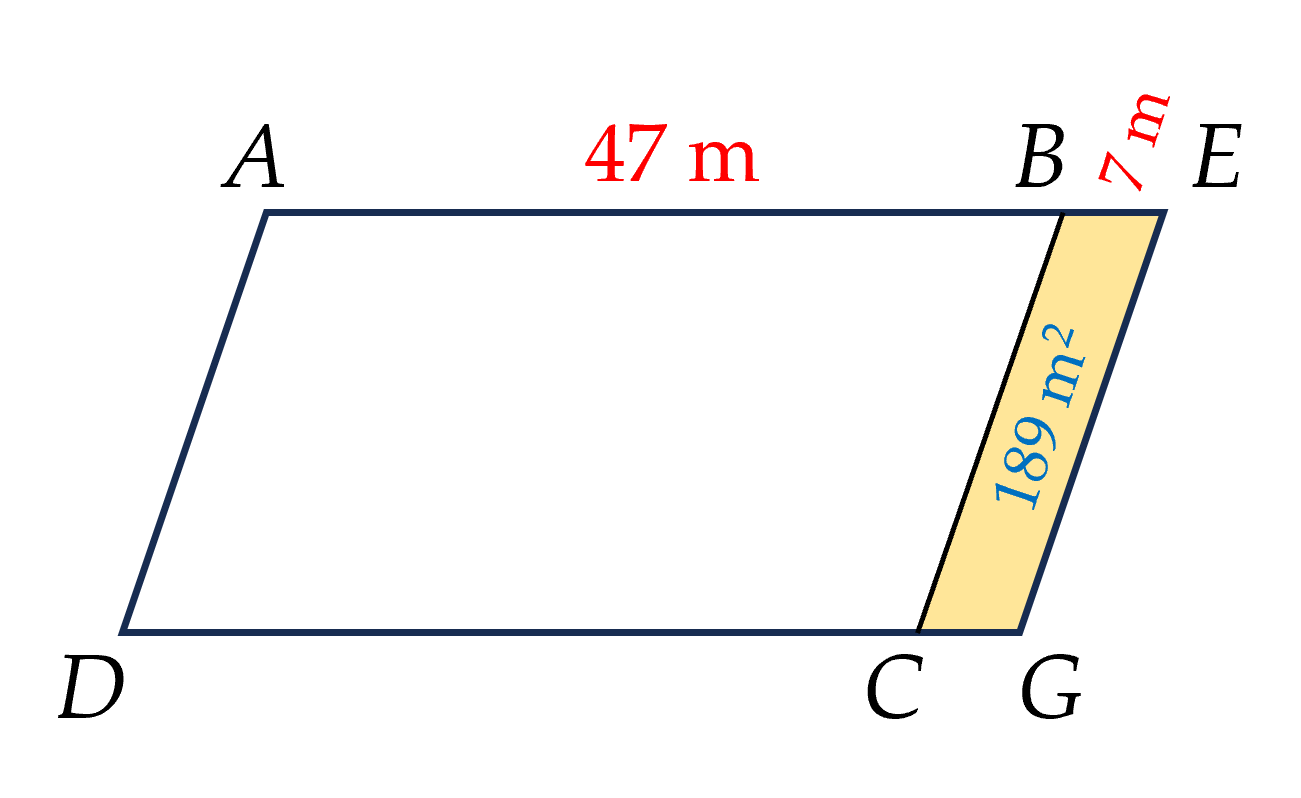
Một mảnh đất có dạng hình bình hành $ABCD$ với $AB = 47$ m. Người ta mở rộng mảnh đất này thành hình hành $AEGD$ có diện tích lớn hơn diện tích ban đầu là $189$ m$^2$ và $BE = 7$ m. Tính diện tích mảnh đất ban đầu.
Hướng dẫn giải:
Chiều cao hình bình hành $BCGE$ là:
$189$ : $7 = 27$ (m)
Diện tích hình bình hành $ABCD$ ban đầu là:
$47. 27 = 1$ $269$ (m$^2$).
