Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

1) Số tiền bác Mai phải trả khi mua $5$ chai dung dịch sát khuẩn là:

$5.80 \, 000=400 \, 000$ (đồng)

Số tiền bác Mai phải trả khi mua $3$ hộp khẩu trang là: $3.x$ (đồng)

Đa thức $F(x)$ biểu thị tổng số tiền bác Mai phải thanh toán là: $400 \, 000+3 x$ (đồng)

2)

a) Ta có: $A(x)=2 x^2-3 x+5+4 x-2 x^2=\left(2 x^2-2 x^2\right)+(-3 x+4 x)+5=x+5$

Bậc: $1$; hệ số cao nhất: $1$; hệ số tự do: $5$.

b) Ta có: $C(x) =(x-1) . A(x)+B(x)=(x-1)(x+5)+\left(x^2-2 x+5\right)=x^2+4 x-5+x^2-2 x+5 $ $=\left(x^2+x^2\right)+(4 x-2 x)+(-5+5)=2 x^2+2 x$.

Hướng dẫn giải:

a) Biến cố ${A}$ là biến cố ngẫu nhiên, biến cố ${B}$ là biến cố chắc chắn, biến cố ${C}$ là biến cố không thể.

b) Xác suất của biến cố $A$ là: $\dfrac{3}{6}=\dfrac{1}{2}$.

Hướng dẫn giải:

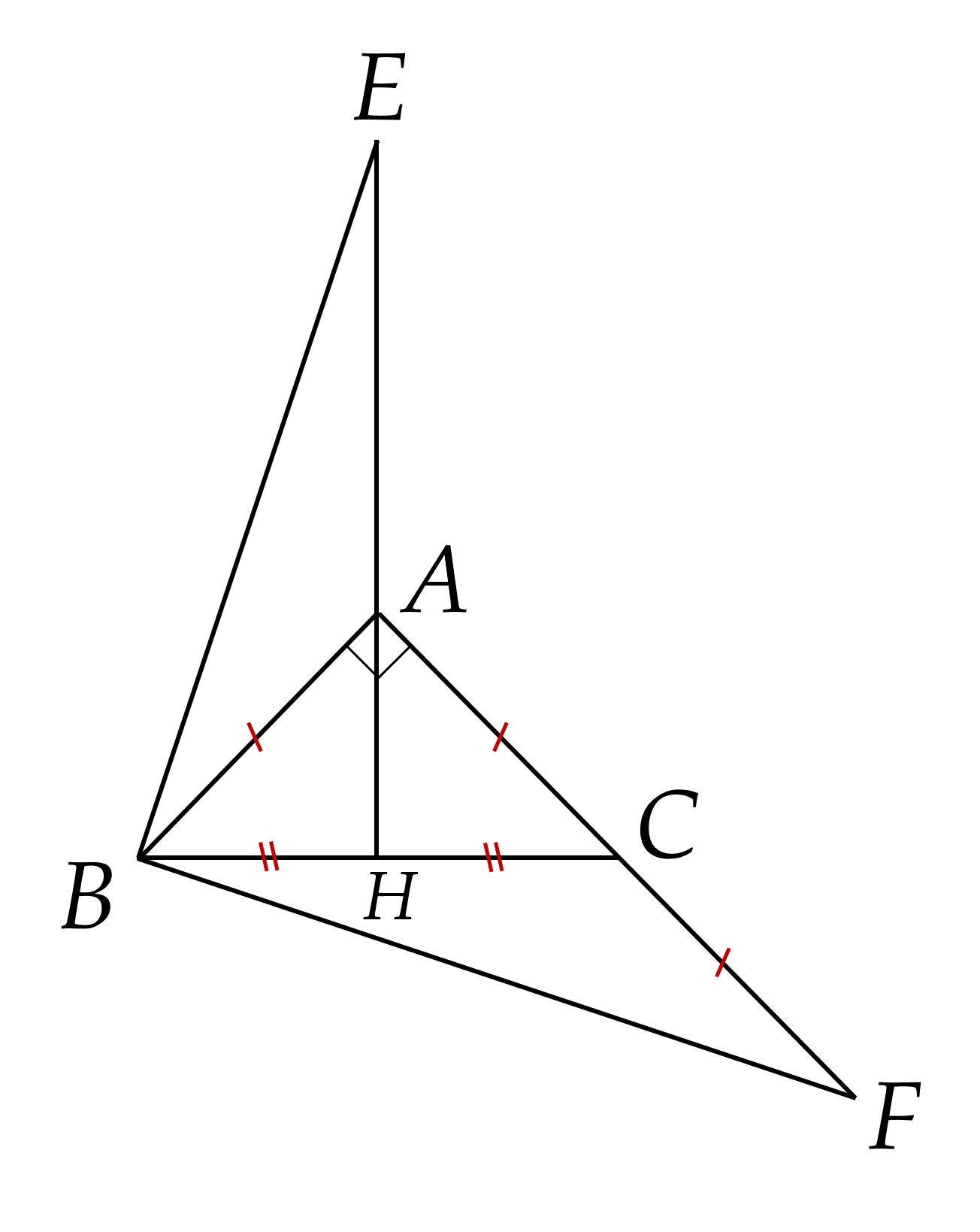
a) Xét $\Delta AHB$ và $\Delta AHC$ có:

$AB=AC$ (gt);

$AH$ chung;

$HB=HC$ ($H$ là trung điểm của $BC$);

Suy ra $\Delta A H B=\Delta A H C $ (c.c.c).

b) Vì $\Delta {AHB}=\Delta {AHC}$ (cmt) suy ra $\widehat{AHB}=\widehat{AHC}$ (cặp góc tương ứng).

Mà $\widehat{AHB}+\widehat{AHC}=180^{\circ}$ (hai góc kề bù).

Suy ra $\widehat{AHB}=\widehat{AHC}=90^{\circ}$.

Vậy $A H \perp B C$.

c) Vi $\Delta {AHB}=\Delta {AHC}$ (cmt) suy ra $\widehat{HAB}=\widehat{HAC}=45^{\circ}$;

$\widehat{HCA}=\widehat{HBA}=\dfrac{180^{\circ}-\widehat{BAC}}{2}=45^{\circ}$ (cặp góc tương ứng).

Xét $\Delta E B A$ và $\Delta B F C$ có:

${AB}={CF}$ (gt);

$\widehat{BAE}=\widehat{BCF}$ (cùng bù với $\widehat{HAB}=\widehat{HCA}=45^{\circ}$);

${EA}={BC}$ (gt);

Suy ra $\Delta {EBA}=\Delta {BFC}$ (c.g.c).

Vậy $BE=BF$ (cặp cạnh tương ứng).

Hướng dẫn giải:

Tại $x=9$ thì:

$ C=x^{14}-10 x^{13}+10 x^{12}-10 x^{11}+...+10 x^2-10 x+10$

$C=x^{14}-(x+1) x^{13}+(x+1) x^{12}-(x+1) x^{11}+...+(x+1) x^2-(x+1) x+x+1$

$C=x^{14}-x^{14}-x^{13}+x^{13}+x^{12}-x^{12}-x^{11}+...+x^3+x^2-x^2-x+x+1 $

$C=1$.

Vậy tại $x=9$ thì giá trị của $C$ bằng $1$.