Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Thực hiện phép tính một cách hợp lí (nếu có thể):
a) $\dfrac{5}{4}-{{\Big(\dfrac{1}{2} \Big)}^{2}}$
b) $\dfrac{2}{3}\cdot \dfrac{-3}{2}+\dfrac{-7}{2}\cdot \dfrac{2}{3}$
c) $\Big(\dfrac{1}{5}+\dfrac{4}{13} \Big)+\Big(\dfrac{-2}{5}+\dfrac{7}{13} \Big)-\Big(\dfrac{4}{5}-\dfrac{2}{13} \Big)$
Hướng dẫn giải:
a) $\dfrac{5}{4}-{{\Big(\dfrac{1}{2} \Big)}^{2}}=\dfrac{5}{4}-\dfrac{1}{4}=1$
b) $\dfrac{2}{3}. \dfrac{-3}{2}+\dfrac{-7}{2}. \dfrac{2}{3}$
$=\dfrac{2}{3}.\Big(\dfrac{-3}{2}+\dfrac{-7}{2} \Big)$
$=\dfrac{2}{3}. (-5 )=\dfrac{-10}{3}$
c) $\Big(\dfrac{1}{5}+\dfrac{4}{13} \Big)+\Big(\dfrac{-2}{5}+\dfrac{7}{13} \Big)-\Big(\dfrac{4}{5}-\dfrac{2}{13} \Big)$
$=\dfrac{1}{5}+\dfrac{4}{13}-\dfrac{2}{5}+\dfrac{7}{13}-\dfrac{4}{5}+\dfrac{2}{13}$
$=\Big(\dfrac{1}{5}-\dfrac{2}{5}-\dfrac{4}{5} \Big)+\Big(\dfrac{4}{13}+\dfrac{7}{13}+\dfrac{2}{13}\Big) =-1+1=0 $
Tìm $x$, biết:
a) $x+\dfrac{1}{2}=\dfrac{6}{4}$
b) ${{x}^{4}}{{.3}^{5}}={{27}^{3}}$
c) $\dfrac{8}{3}.\Big(\dfrac{5}{24}-x \Big)=\dfrac{-1}{3}$
Hướng dẫn giải:
a) $x+\dfrac{1}{2}=\dfrac{6}{4}$
$x=\dfrac{6}{4}-\dfrac{1}{2} $
$x=\dfrac{6}{4}-\dfrac{2}{4}=1$
b) ${{x}^{4}}{{.3}^{5}}={{27}^{3}}$
${{x}^{4}}{{.3}^{5}}={{({{3}^{3}})}^{3}}$
${{x}^{4}}{{.3}^{5}}={{3}^{9}}$
${{x}^{4}}={{3}^{9}}:{{3}^{5}}={{3}^{4}}$
$x=3$
c) $\dfrac{8}{3}.\Big(\dfrac{5}{24}-x \Big)=\dfrac{-1}{3}$
$ \dfrac{5}{24}-x=\dfrac{-1}{3}:\dfrac{8}{3}$
$\dfrac{5}{24}-x=\dfrac{-1}{8}$
$x=\dfrac{5}{24}+\dfrac{1}{8}=\dfrac{8}{24}=\dfrac{1}{3}$
a) Tính thể tích của hình hộp chữ nhật có kích thước dưới đây.
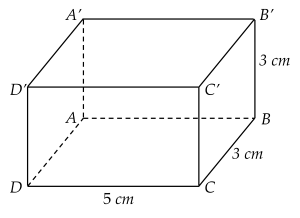
b) Tính thể tích và diện tích xung quanh của hình lăng trụ đứng tứ giác dưới đây, biết đáy là một hình thang vuông.

Hướng dẫn giải:
a) Thể tích của hình hộp chữ nhật là: $5.3.3 = 45$ (cm3)
b)
Thể tích của hình lăng trụ đứng tam giác là: $\dfrac{(3+4).3}{2}.5=52,5$ (cm3)
Diện tích xung quanh của hình lăng trụ đứng tam giác là:
$(3 + 4 + 3 + 4).5 = 70$ (cm2)
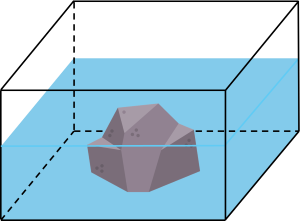
Một bể cá có chiều dài $1$ m, chiều rộng $60$ cm, mực nước trong bể cao $60$ cm. Khi bỏ một tảng đá vào bể cá thì mực nước trong bể tăng lên $5$ cm (biết rằng tảng đá ngập hoàn toàn trong nước). Tính thể tích của tảng đá đó.
Hướng dẫn giải:
Thể tích nước tăng lên chính là thể tích tảng đá.
Chiều cao nước sau khi bỏ tảng đá là: $60 + 5 = 65$ (cm)
Đổi $60$ cm $= 0,6$ m; $65$ cm $= 0,65$ m
Thể tích nước ban đầu trong bể là: $1.0,6.0,6 = 0,36$ (m3)
Thể tích nước trong bể sau khi bỏ tảng đá là: $1.0,6.0,65 = 0,39$ (m3)
Thể tích tảng đá là: $0,39 – 0,36 = 0,03$ (m3)
Bình đọc một cuốn sách trong $4$ ngày. Ngày thứ nhất đọc được $\dfrac{1}{6}$ quyển sách, ngày thứ hai đọc được $\dfrac{1}{4}$ quyển sách, ngày thứ ba đọc được $\dfrac{1}{5}$ quyển sách. Hỏi hai ngày đầu Bình đọc nhiều hơn hay ít hơn hai ngày sau? Tìm phân số chỉ số chênh lệch đó.
Hướng dẫn giải:
Phân số chỉ số trang sách đọc được trong ngày thứ tư là:
$1-\Big(\dfrac{1}{6}+\dfrac{1}{4}+\dfrac{1}{5} \Big)$
$=1-\Big(\dfrac{10}{60}+\dfrac{15}{60}+\dfrac{12}{60} \Big)$
$=1-\dfrac{37}{60}=\dfrac{23}{60}$ (quyển sách)
Phân số chỉ số trang sách đọc được trong hai ngày đầu là:
$\dfrac{1}{6}+\dfrac{1}{4}=\dfrac{5}{12}$ (quyển sách)
Phân số chỉ số trang sách đọc được trong hai ngày sau là:
$\dfrac{1}{5}+\dfrac{23}{60}=\dfrac{7}{12}$ (quyển sách)
Hai ngày đầu Bình đọc ít hơn hai ngày sau.
Phân số chỉ số chênh lệch đó là:
$\dfrac{7}{12}-\dfrac{5}{12}=\dfrac{2}{12}=\dfrac{1}{6}$ (quyển sách)
Cho biểu thức $A=\dfrac{1}{1.2}+\dfrac{1}{3.4}+\dfrac{1}{5.6}+...+\dfrac{1}{99.100}$. Chứng minh rằng $A<1$.
Hướng dẫn giải:
$A=\dfrac{1}{1.2}+\dfrac{1}{3.4}+\dfrac{1}{5.6}+...+\dfrac{1}{99.100}$
$A=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}$
$A=\Big(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{99}+\dfrac{1}{100} \Big)-2\Big(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{100} \Big)$
$A=\Big(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{99}+\dfrac{1}{100}\Big)-\Big(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{50} \Big)$
$ A=\dfrac{1}{51}+\dfrac{1}{52}+\dfrac{1}{53}+...+\dfrac{1}{100}$
Tổng $A$ có $50$ số hạng, ta có: $A<\dfrac{1}{50}.50=1$
