Phần tự luận (7 điểm) SVIP

Bài 1. (0,5 điểm) Cho hai đa thức $A=x^2-3xy-y^2+1$ và $B=2x^2+y^2-7xy-5$.

a) Tính $A+B$.

b) Tìm đa thức $C$ biết $C+A-B=0$.

c) Tính giá trị của đa thức $C$ với $x=2,\,\,y=\dfrac{-1}{2}$.

Bài 2. (2 điểm)

a) Chứng minh giá trị của biểu thức $ A$ không phụ thuộc vào giá trị của biến.

$A=x(2x-3)+2x^2(x-2)-2x(x^2-x+1)+(5x^2-5x):x$

b) Tìm $x$, biết: $(1-x)(1+x+x^2)+x(x^2-5)=11$.

Bài 3. (2 điểm) Phân tích đa thức sau thành nhân tử:

a) $5x^2+10xy-4x-8y$;

b) $4x^2+4x-y^2+1$.

Bài 4. (0,5 điểm)

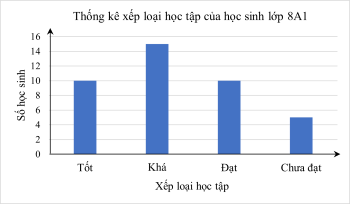
Thống kê xếp loại học tập của học sinh lớp 8A1

Lựa chọn biểu đồ phù hợp biểu diễn bảng thống kê trên. Vẽ biểu đồ đó.

Bài 5. (0,5 điểm) Đèn đá muối Himalaya là một loại đèn độc đáo có bộ phận chụp đèn làm từ tinh thể muối. Hình dưới là một chiếc chụp đèn đá muối có dạng hình chóp tứ giác đều (không tính phần chân để của đèn). Biết mặt bên của chụp đèn là một tam giác đều có cạnh bằng $20$ cm, đường cao của các mặt bên bằng $22,4$ cm. Tính diện tích xung quanh của phần chụp đèn.

Bài 6. (0,5 điểm) Chứng minh không tồn tại $x,\,y$ thỏa mãn:

$4x^2+2y^2+2y-4xy+5=0$