Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Câu 13. (1 điểm) Khai triển mỗi hằng đẳng thức sau.
a) $(2x-3)^2$;
b) $(x-2)^3$.
Hướng dẫn giải:
a) $(2x-3)^2 = 4x^2 - 12x + 9$;
b) $(x-2)^3 = x^3 -6x^2 + 12x - 8$.
Câu 14 (1 điểm). Phân tích các đa thức sau thành nhân tử:
a) $x^3 + 8y^3$;
b) $x^2 + 2xy +y^2 - 4$.
Hướng dẫn giải:
Phân tích các đa thức sau thành nhân tử:
a) $x^3 + 8y^3$
$=(x+2y)(x^2 - 2xy + 4y^2)$
b) $x^2 + 2xy +y^2 - 4$
$=(x+y)^2 - 2^2$
$=(x+y+2)(x+y-2)$
Câu 15 (1 điểm). Tìm $x$ biết:
a) $x(x+1) - (x+1)^2 = 5$;
b) $x^2 - 4x = 0$.
Hướng dẫn giải:
a) $x(x+1) - (x+1)^2 = 5$
$x^2 + x - (x^2+2x+1) = 5$
$x^2 + x - x^2 - 2x - 1= 5$
$ x - 2x - 1= 5$
$ - x = 6$
$ x = -6$
b) $x^2 - 4x = 0$.
$x(x-4) = 0$
$x = 0$ hoặc $x=4$.
Câu 16 (2,5 điểm). Cho hình thoi $ABCD$ có $\widehat{A}=60^{\circ}$. Vẽ $BH$ vuông góc với cạnh $AD$, trên tia đối của $HB$ lấy điểm $E$ sao cho ${HE}={BH}$. Nối $E$ với ${A}, {E}$ với $D$.
a) Chứng minh rằng $ABDE$ là hình thoi.
b) Ba điểm ${E}, {D}, {C}$ thẳng hàng.
c) ${EB}={AC}$.
Hướng dẫn giải:
| GT | Hình thoi $ABCD$ có $\widehat{A} = 60^{\circ}$, Vẽ $BH$ vuông góc với cạnh $AD$, trên tia đối của $HB$ lấy điểm $E$ sao cho $HE = BH$. Nếu $E$ với $A$, $E$ với $D$. |
| KL | a) Chứng minh rằng $ABDE$ là hình thoi. b) Ba điểm $E,D,C$ thẳng hàng. c) $EB = AC$. |

a) Vì $ABCD$ là hình thoi nên $AB = BC = CD = DA$.
Xét tam giác $ABD$, ta có $AB = AD$, do đó tam giác $ABD$ là tam giác cân. Mặt khác $\widehat{BAD} = 60^{\circ}$. Từ đó suy tam giác $ABD$ là tam giác đều.
Trong tam giác $ABD$ đều, có đường cao $BH$, vậy BH cũng là đường trung tuyến của tam giác $ABD$, hay H là trung điểm của $AD$.
Tứ giác $ABDE$ có hai đường chéo $AD$ và $BE$ cắt nhau tại trung điểm $H$ của mỗi đường, suy ra $ABDE$ là hình bình hành.
Mặt khác, ta có $BH \perp AD$ nên ta suy ra $ABDE$ là hình thoi.
b) Vì $ABDE$ là hình thoi nên $AB // DE$.
Vì $ABCD$ là hình thoi nên $AB // CD$.
Từ hai điều trên, theo tiên đề Euclid, ta suy ra $DE // CD.$
c)

Vì tam giác $ABD$ đều nên $\widehat{ABD} = 60^{\circ}$.
$ABCD$ là hình thoi nên $\widehat{BAD} = \widehat{AED} = 60^{\circ}$.
$ABDE$ là hình thoi nên $\widehat{ABD} = \widehat{BCD} = 60^{\circ}$.
Xét tứ giác $ABCE$ có:
+) $AB // CE$
+) $\widehat{AED} = \widehat{BCD} = 60^{\circ}$.
Suy ra tứ giác $ABCE$ là hình thang cân. Do đó, $EB = AC$ (hai đường chéo bằng nhau).
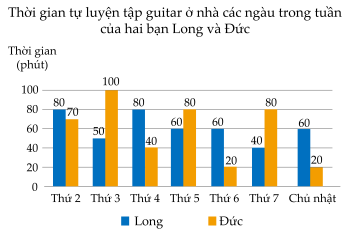
Câu 17 (1,5 điểm). Thời gian (tính theo phút) tự luyện tập guitar ở nhà các ngày trong tuần của 2 bạn Long và Đức cho bởi bảng thống kê dưới đây.
| Thứ 2 | Thứ 3 | Thứ 4 | Thứ 5 | Thứ 6 | Thứ 7 | Chủ nhật | |
| Long | $80$ | $50$ | $80$ | $60$ | $60$ | $40$ | $60$ |
| Đức | $70$ | $100$ | $40$ | $80$ | $20$ | $80$ | $20$ |
Nêu biểu đồ thích hợp biểu diễn bảng số liệu trên.
Hướng dẫn giải:
Biểu đồ cột kép là biểu đồ thích hợp biểu diễn bảng số liệu trên.