Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

Phương trình đã cho có $a-b+c=0$.

Suy ra phương trình có hai nghiệm $x=-1$ và $x=2$.

Hướng dẫn giải:

$\left\{ \begin{aligned} & 3x-y=-4 \\ & 2x+3y=1 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & 6x-2y=-8 \\ & 6x+9y=3 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & 11y=11 \\ & 2x+3y=1 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} &x=-1  \\ &y=1  \\ \end{aligned} \right.$

Hướng dẫn giải:

Phương trình hoành độ giao điểm của $\left( d \right)$ và $(P)$ là:

${{x}^{2}}=2x-m \Leftrightarrow {{x}^{2}}-2x+m=0$ (1)

Ta có: ${{\Delta }^{'}}=1-m$.

Điều kiện để $\left( d \right)$ cắt $(P)$ tại hai điểm phân biệt là phương trình hoành độ giao điểm của $\left( d \right)$ và $(P)$ có hai nghiệm phân biệt.

Suy ra $1-m>0\Leftrightarrow m<1$ (*).

Khi đó $x_1$, $x_2$ là các hoành độ giao điểm của $(d)$ và $(P)$ nên $x_1$, $x_2$ là các nghiệm của phương trình hoành độ của $(d)$ và $(P)$.

Theo hệ thức Vi-et ta có: $\left\{ \begin{aligned} & x_1+x_2 = 2 \\ & x_1x_2=m \\ \end{aligned} \right.$

Khi đó, ${{y}_{1}}+{{y}_{2}}+{{x}_{1}}^{2}{{x}_{2}}^{2}=6\left( {{x}_{1}}+{{x}_{2}} \right).$

$\Leftrightarrow {{x}_{1}}^{2}+{{x}_{2}}^{2}+{{x}_{1}}^{2}{{x}_{2}}^{2}=6\left( {{x}_{1}}+{{x}_{2}} \right).$

$\Leftrightarrow {{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-2{{x}_{1}}{{x}_{2}}+{{x}_{1}}^{2}{{x}_{2}}^{2}=6\left( {{x}_{1}}+{{x}_{2}} \right).$

$\Leftrightarrow 4-2m+{{m}^{2}}=12\Leftrightarrow {{m}^{2}}-2m-8=0\Leftrightarrow \left[ \begin{aligned} & m=-2 \, \, \left( \text{tm} \, \left( * \right) \right) \\ & m=4 \, \, \left( \text{ktm} \, \left( * \right) \right) \\ \end{aligned} \right.$

Vậy $m=-2$ là giá trị cần tìm.

Hướng dẫn giải:

Gọi thời gian đội $A$ và đội $B$ làm một mình xong công việc lần lượt là $x,$ $y$ (ngày).

ĐK $x$, $y>12$.

Mỗi ngày, đội $A$ làm được  $\dfrac{1}{x}$ công việc.

Mỗi ngày, đội $B$ làm được  $\dfrac{1}{y}$ công việc.

Mỗi ngày, hai đội làm được  $\dfrac{1}{12}$ công việc.

Ta có phương trình $\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}$ (1)

Trong $8$ ngày làm chung, hai đội làm được $\dfrac{2}{3}$ công việc.

Trong $8$ ngày tiếp theo, do tăng năng suất gấp đôi nên đội $B$ làm được $\dfrac{16}{y}$ công việc.

Ta có phương trình: $\dfrac{2}{3}+\dfrac{16}{y}=1$ (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{ \begin{aligned} &\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}  \\ &\dfrac{2}{3}+\dfrac{16}{y}=1\,  \\ \end{aligned} \right.\,\,\,\Leftrightarrow \left\{ \begin{aligned} &\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}  \\ &\dfrac{16}{y}=\dfrac{1}{3}\,  \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & \dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}  \\ &y=48\,  \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} &x=16  \\ &y=48\,  \\ \end{aligned} \right.\,\,\left( \text{tm} \right)$.

Vậy thời gian đội $A$ và đội $B$ làm một mình xong công việc lần lượt là $16;\,\,48$ (ngày).

Hướng dẫn giải:

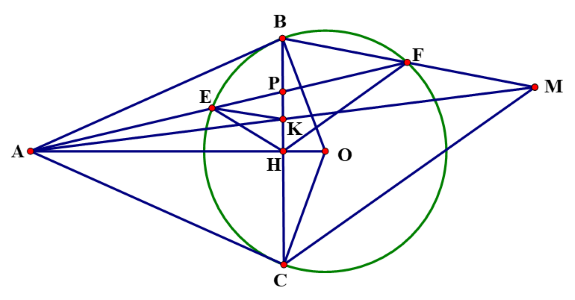
a) Vì $AB$, $AC$ là các tiếp tuyến của $(O)$ nên $\widehat{ABO} = \widehat{ACO} = 90^{\circ}$.

Xét tứ giác $ABOC$ có $\widehat{ABO} + \widehat{ACO} = 90^{\circ} + 90^{\circ} = 180^{\circ}$ nên tứ giác $ABOC$ nội tiếp đường tròn.

b) Xét $\Delta ABE$ và $\Delta AFB$ có:

$\widehat{ABE} = \widehat{BAE} = \dfrac12\text{sđ} \overset\frown{EB}$

$\widehat{BAE}$ là góc chung.

Do đó, $\Delta ABE\,\backsim \,\Delta AFB$.

Suy ra, $\dfrac{AB}{{AF}}=\dfrac{AE}{AB}\Rightarrow A{{B}^{2}}=AE.{AF}$ (1)

$\left. \begin{aligned} & OB=OC \, \, (GT) \\ & AB=AC \\ \end{aligned} \right\}\Rightarrow $ $AO$ là trung trực của $BC$

$\Rightarrow \, AO\bot BH$.

$\Delta ABO$ vuông tại $B$, đường cao $BH$ nên $A{{B}^{2}}=AH.{AO}$ (2).

Từ (1) và (2) ta có $AE.{AF}=AH.{AO}\,\Rightarrow \dfrac{AE}{AO}=\dfrac{AH}{{AF}}$.

Suy ra $\Delta AEH\, \backsim \,\Delta A{OF}\,\left( {c}{.g}{.c} \right)$

$\Rightarrow \widehat{AHE}=\widehat{{AFO}}$

$\Rightarrow EHOF$ nội tiếp.

$\Rightarrow \widehat{OHF}=\widehat{{OEF}}$

c) Gọi giao điểm của $BC$ và  ${AF}$ là $P$

${EK//BM}\Rightarrow \dfrac{{EK}}{{FM}}=\dfrac{AE}{{AF}} , \, \, \dfrac{{EK}}{{BF}}=\dfrac{EP}{{FP}}$ (3)

Lại có: $\widehat{{OHF}}=\widehat{{OEF}}$ (cmt);

$\widehat{{OFE}}=\widehat{{OEF}}\,\,$( $\Delta {OEF}$ cân); $\widehat{AHE}=\widehat{{EFO}}$ (cmt)

Suy ra $\widehat{AHE}=\widehat{{FHO}}\,\,$

Mà $\widehat{AHE}+\widehat{EHB}=\widehat{{FHO}}\,+\widehat{FHB}={{90}^{\circ}}$

$\Rightarrow \widehat{EHB}=\widehat{FHB}\,\,\Rightarrow $ $HB$ là tia phân giác $\widehat{EHF}$ $\Rightarrow \,\,\dfrac{EP}{FP}=\dfrac{EH}{FH}$ (4)

$\Delta EHF$ có $HB$ là phân giác trong $\widehat{EHF}$, $HP\bot \,HA$ nên $HA$ là đường phân giác góc ngoài của $\widehat{EHF}$

$\Rightarrow \,\,\dfrac{EA}{FA}=\dfrac{EP}{FP}$ (5)

Từ (3), (4) và (5) suy ra: $\dfrac{{EK}}{{FM}}=\,\,\dfrac{{EK}}{{BF}}\Rightarrow BF=FM$

$\Rightarrow \,\,HF$ là đường trung bình $\Delta BCM\Rightarrow \,\,CM=2HF$.

Hướng dẫn giải:

Bất đẳng thức cần chứng minh tương đương với $\dfrac{a}{{{b}^{3}}}+\dfrac{b}{{{c}^{3}}}+\dfrac{c}{{{a}^{3}}}\ge a+b+c$.

$0<abc\le 1\Rightarrow \dfrac{a}{{{b}^{3}}}+\dfrac{b}{{{c}^{3}}}+\dfrac{c}{{{a}^{3}}}\ge \dfrac{{{a}^{2}}c}{{{b}^{2}}}+\dfrac{{{b}^{2}}a}{{{c}^{2}}}+\dfrac{{{c}^{2}}b}{{{a}^{2}}}$.

Do đó ta cần chứng minh $\dfrac{a}{{{b}^{3}}}+\dfrac{b}{{{c}^{3}}}+\dfrac{c}{{{a}^{3}}}\ge \dfrac{{{a}^{2}}c}{{{b}^{2}}}+\dfrac{{{b}^{2}}a}{{{c}^{2}}}+\dfrac{{{c}^{2}}b}{{{a}^{2}}}\ge a+b+c$ (*).

Sử dụng bất đẳng thức AM – GM ta được: $\begin{aligned} & \dfrac{{{a}^{2}}c}{{{b}^{2}}}+\dfrac{{{b}^{2}}a}{{{c}^{2}}}+c\ge 3\sqrt[3]{\dfrac{{{a}^{2}}c}{{{b}^{2}}}.\dfrac{{{b}^{2}}a}{{{c}^{2}}}.c}=3a\, \\ & \dfrac{{{b}^{2}}a}{{{c}^{2}}}+\dfrac{{{c}^{2}}b}{{{a}^{2}}}+a\ge 3\sqrt[3]{\dfrac{{{b}^{2}}a}{{{c}^{2}}}.\dfrac{{{c}^{2}}b}{{{a}^{2}}}.a}=3b\, \\ & \dfrac{{{a}^{2}}c}{{{b}^{2}}}+\dfrac{{{c}^{2}}b}{{{a}^{2}}}+b\ge 3\sqrt[3]{\dfrac{{{a}^{2}}c}{{{b}^{2}}}.\dfrac{{{c}^{2}}b}{{{a}^{2}}}.b}=3c\, \\ \end{aligned}$.

Cộng từng vế các bất đẳng thức trên và thu gọn ta được: $\dfrac{{{a}^{2}}c}{{{b}^{2}}}+\dfrac{{{b}^{2}}a}{{{c}^{2}}}+\dfrac{{{c}^{2}}b}{{{a}^{2}}}\ge a+b+c\,\,$.

Dấu bằng xảy ra khi $a=b=c=1$.