Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
(1,5 điểm) a) Chứng minh đẳng thức: $\left( 2-\dfrac{3+\sqrt{3}}{\sqrt{3}+1} \right).\left( 2+\dfrac{3-\sqrt{3}}{\sqrt{3}-1} \right)=1.$
b) Rút gọn biểu thức $A=\left( \dfrac{1}{x-2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2} \right):\dfrac{\sqrt{x}+1}{x-4\sqrt{x}+4}$ với $x>0;$ $x\ne 4$.
Hướng dẫn giải:
Ta có: $\left( 2-\dfrac{3+\sqrt{3}}{\sqrt{3}+1} \right).\left( 2+\dfrac{3-\sqrt{3}}{\sqrt{3}-1} \right)$
$=\left( 2-\dfrac{\sqrt{3}\left( \sqrt{3}+1 \right)}{\sqrt{3}+1} \right).\left( 2+\dfrac{\sqrt{3}\left( \sqrt{3}-1 \right)}{\sqrt{3}-1} \right)$
$=\left( 2-\sqrt{3} \right).\left( 2+\sqrt{3} \right)=4-3=1$
Vậy đẳng thức được chứng minh.
b) Với $x>0;$ $x\ne 4$:
$A=\left( \dfrac{1}{x-2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2} \right):\dfrac{\sqrt{x}+1}{x-4\sqrt{x}+4}$
$=\left( \dfrac{1}{\sqrt{x}\left( \sqrt{x}-2 \right)}+\dfrac{1}{\sqrt{x}-2} \right):\dfrac{\sqrt{x}+1}{{{\left( \sqrt{x}-2 \right)}^{2}}}$
$=\dfrac{1+\sqrt{x}}{\sqrt{x}\left( \sqrt{x}-2 \right)}.\dfrac{{{\left( \sqrt{x}-2 \right)}^{2}}}{\sqrt{x}+1}=\dfrac{\sqrt{x}-2}{\sqrt{x}}$.
Vậy với $x>0;$ $x\ne 4$, $A=\dfrac{\sqrt{x}-2}{\sqrt{x}}$.
(1,5 điểm) a) Tìm tọa độ của tất cả các điểm thuộc parabol $y=-2{{x}^{2}}$ có tung độ bằng $-8$.
b) Cho phương trình ${{x}^{2}}-2\left( m+1 \right)x+{{m}^{2}}+2m=0$ (với $m$ là tham số). Tìm tất cả các giá trị của $m$ để phương trình có hai nghiệm phân biệt ${{x}_{1}};$ ${{x}_{2}}$ (với ${{x}_{1}}<{{x}_{2}}$) thỏa mãn: $\left| {{x}_{1}} \right|=3\left| {{x}_{2}} \right|$.
Hướng dẫn giải:
a) Thay $y=-8$ vào phương trình parabol: $y=-2{{x}^{2}}$.
Ta có: $-2{{x}^{2}}=-8\Leftrightarrow {{x}^{2}}=4\Leftrightarrow x=\pm 2$.
Vậy tọa độ tất cả các điểm thỏa mãn đề bài là $\left( 2;-8 \right)$ và $\left( -2;-8 \right)$.
b) Phương trình: ${{x}^{2}}-2\left( m+1 \right)x+{{m}^{2}}+2m=0$ (1)
Phương trình (1) là phương trình bậc hai ẩn $x$ có:
$\Delta '={{\left[ -\left( m+1 \right) \right]}^{2}}-\left( {{m}^{2}}+2m \right)={{m}^{2}}+2m+1-{{m}^{2}}-2m=1$>0.
Phương trình có hai nghiệm phân biệt ${{x}_{1}};$ ${{x}_{2}}$ với mọi $m$, mà ${{x}_{1}}<{{x}_{2}}$ nên:
${{x}_{1}}=m+1-1=m$;
${{x}_{2}}=m+1+1=m+2$.
${{x}_{1}};$ ${{x}_{2}}$ thỏa mãn: $\left| {{x}_{1}} \right|=3\left| {{x}_{2}} \right|$$\Rightarrow \left| m \right|=3\left| m+2 \right|$
$\Leftrightarrow \left[ \begin{aligned} & m=3\left( m+2 \right) \\ & m=-3\left( m+2 \right) \\ \end{aligned} \right.\Leftrightarrow \left[ \begin{aligned} & 3m+6=m \\ & m=-3m-6 \\ \end{aligned} \right.\Leftrightarrow \left[ \begin{aligned} & m=-3\left( \, \text{tm} \right) \\ & m=\dfrac{-3}{2}\left( \, \text{tm} \right) \\ \end{aligned} \right.$
Vây tất cả các giá trị của $m$ thỏa mãn đề bài là $m=-3$ và $m=-\dfrac{3}{2}$.
(1,0 điểm) Giải hệ phương trình $\left\{ \begin{aligned} & \dfrac{x}{y}+2\cdot \dfrac{y}{x}=3 \\ & 2{{x}^{2}}-3y=-1 \\ \end{aligned} \right.$.
Hướng dẫn giải:
Điều kiện: $x;$ $y\ne 0$
Đặt $\dfrac{x}{y}=t$ khi đó hệ trở thành $\left\{ \begin{aligned} & t+\dfrac{2}{t}=3 \, \left( 1 \right) \\ & 2{{x}^{2}}-3y=-1 \, \left( 2 \right) \\ \end{aligned} \right.$
Giải $\left( 1 \right)$ ta được:
${{t}^{2}}-3t+2=0\Leftrightarrow \left( t-1 \right)\left( t-2 \right)=0\Leftrightarrow \left[ \begin{aligned} & t=1 \\ & t=2 \\ \end{aligned} \right.$
+ Với $t=1\Rightarrow \dfrac{x}{y}=1\Leftrightarrow x=y$ thế vào $\left( 2 \right)$ ta được:
$2{{x}^{2}}-3x+1=0\Leftrightarrow \left( x-1 \right)\left( 2x-1 \right)=0\Leftrightarrow \left[ \begin{aligned} & x=1 \\ & x=\dfrac{1}{2} \\ \end{aligned} \right.$ (thỏa mãn điều kiện)
Vậy suy ra $y=1;$ $y=\dfrac{1}{2}$.
Do đó hệ phương trình có nghiệm là $\left( x;y \right)= \left( 1;1 \right);$ $\left( x;y \right)=\left( \dfrac{1}{2};\dfrac{1}{2} \right)$.
+ Với $t=2\Rightarrow \dfrac{x}{y}=2\Leftrightarrow x=2y$ thế vào $\left( 2 \right)$ ta được:
$2{{\left( 2y \right)}^{2}}-3y+1=0\Leftrightarrow 8{{y}^{2}}-3y+1=0$.
Do $\Delta =-23<0$ nên phương trình vô nghiệm.
Vậy hệ phương trình có nghiệm là $\left( x;y \right)= \left( 1;1 \right);$ $\left( x;y \right)=\left( \dfrac{1}{2};\dfrac{1}{2} \right)$.
(3,0 điểm) 1. Mảnh đất hình chữ nhật $ABCD$ có chiều dài $AB=6$ m, chiều rộng $BC=4$ m. Người ta trồng hoa trên phần đất là nửa hình tròn đường kính $AD$ và nửa đường tròn đường kính $BC$, phần còn lại của mảnh đất để trồng cỏ. Tính diện tích phần đất trồng cỏ (phần tô đậm trong hình vẽ bên dưới, kết quả làm tròn đến chữ số thập phân thứ nhất).

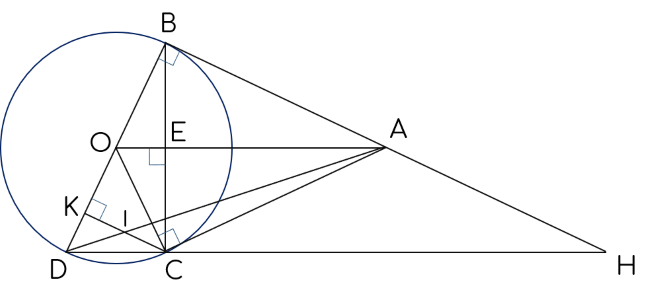
2. Cho $\left( O \right)$ và điểm $A$ nằm bên ngoài đường tròn. Từ $A$ kẻ các tiếp tuyến $AB,$ $AC$ với đường tròn $\left( O \right)$ ($B,$ $C$ là các tiếp điểm). Kẻ đường kính $BD$ của đường tròn $\left( O \right)$.
a) Chứng minh $ABOC$ là tứ giác nội tiếp đường tròn và $\widehat{BDC}=\widehat{AOC}$.
b) Kẻ $CK$ vuông góc với $BD$ tại $K$. Gọi $I$ là giao điểm của $AD$ và $CK$. Chứng minh rằng $I$ là trung điểm của $CK$.
Hướng dẫn giải:
1) Diện tích hình chữ nhật $ABCD$ là $6.4=24$ (m$^{2}$).
Có $ABCD$ là hình chữ nhật $\Rightarrow AD=BC=4$ (m).
Bán kính đường tròn đường kính $AD$ là $\dfrac{AD}{2}=\dfrac{4}{2}=2$ (m).
Diện tích nửa đường tròn đường kính $AD$ là $\dfrac{\pi {{.2}^{2}}}{2}=2\pi$ (m$^{2}$).
Bán kính đường tròn đường kính $BC$ là $\dfrac{BC}{2}=\dfrac{4}{2}=2$ (m).
Diện tích nửa đường tròn đường kính $BC$ là $\dfrac{\pi {{.2}^{2}}}{2}=2\pi$ (m$^{2}$).
Diện tích phần đất trồng cỏ là $24-\left( 2\pi +2\pi \right)\approx 11,4$ (m$^{2}$).
2)
Do $AB,$ $AC$ là các tiếp tuyến của đường tròn $\left( O \right)$ (gt)
$\Rightarrow \left\{ \begin{aligned} & AB\bot OB \\ & AC\bot OC \\ \end{aligned} \right.$ (Tính chất tiếp tuyến)
Từ đó suy ra $\widehat{ABO}=\widehat{ACO}=90^{\circ} $.
Xét tứ giác $ABOC$ có: $\widehat{ABO}+\widehat{ACO}=90^{\circ}+90^{\circ}=180^{\circ}$ và hai góc ở vị trí đối nhau nên tứ giác $ABOC$ nội tiếp đường tròn.
Ta có $AB,$ $AC$ là các tiếp tuyến của đường tròn $\left( O \right)$ (gt)
Suy ra $AB=AC$ (Tính chất tiếp tuyến) nên $A$ thuộc đường trung trực của $BC$.
Lại có $OB=OC=R$ nên suy ra $O$ cũng thuộc đường trung trực của $BC$.
Từ đó suy ra $OA$ là đường trung trực của $BC$ $\Rightarrow OA\bot BC$ (1)
Xét $\left( O \right)$ có $BD$ là đường kính (gt) và $C\in \left( O \right)$.
Suy ra $\widehat{DCB}=90^{\circ}$ (Góc nội tiếp chắn nửa đường tròn)
$\Rightarrow DC\bot BC$ (2)
Từ (1) và (2) suy ra $OA$ // $CD$ (Từ vuông góc đến song song)
$\Rightarrow \widehat{BDC}=\widehat{AOC}$.
b) Kẻ $CD\cap AB$ tại $H$ $\Rightarrow \widehat{HCB}=\widehat{BCD}=90^{\circ}$.
Ta có $\widehat{ACH}+\widehat{ACB}=90^{\circ} $ và $\widehat{AHC}+\widehat{ABC}=90^{\circ}$
Mà $\widehat{ABC}=\widehat{ACB}$ (do tam giác $ABC$ cân)
Từ đó suy ra $\widehat{ACH}=\widehat{AHC}$ $\Rightarrow \Delta ACH$ cân $AH=AC$.
Mà $AB=AC$ nên suy ra $AB=AH=AC$ (3).
Vì $HB$ // $CK$ (Vì cùng vuông góc $BD$)
$\dfrac{CI}{AH}=\dfrac{DI}{DA}=\dfrac{IK}{AB}$ (Định lí Talet) (4).
Từ (3) và (4) suy ra $CI=IK$.
Từ đó suy ra $I$ là trung điểm của $CK$.
(1,0 điểm) 1. Giải phương trình $4x+1-\sqrt{9\left( 2x-1 \right)\left( x+1 \right)}+2\sqrt{2x-1}-2\sqrt{x+1}=0$ (1).
2. Cho các số thực dương $a,$ $b,$ $c$ thỏa mãn $a+b+c=3$. Tìm giá trị nhỏ nhất của biểu thức $P=\dfrac{2021}{\sqrt{ab}+\sqrt{cd}+\sqrt{ac}}-\dfrac{b\sqrt{a}}{1+b}-\dfrac{c\sqrt{b}}{1+c}-\dfrac{a\sqrt{c}}{1+a}$.
Hướng dẫn giải:
1. Điều kiện: $x\ge \dfrac{1}{2}$.
Đặt $\left\{ \begin{aligned} & a=\sqrt{2x-1} \\ & b=\sqrt{x+1} \\ \end{aligned} \right.\Rightarrow \left\{ \begin{aligned} & 2x-1={{a}^{2}} \\ & x+1={{b}^{2}} \\ \end{aligned} \right.\Rightarrow 4x+1={{a}^{2}}+2{{b}^{2}}$.
Khi đó, phương trình (1) trở thành ${{a}^{2}}+2{{b}^{2}}-3ab+2a-2b=0\Leftrightarrow {{a}^{2}}-{{b}^{2}}+3{{b}^{2}}-3ab+2a-2b=0$
$\Leftrightarrow \left( a-b \right)\left( a+b \right)-3b\left( a-b \right)+2\left( a-b \right)=0\Leftrightarrow \left( a-b \right)\left( a+b-3b+2 \right)=0$
$\Leftrightarrow \left[ \begin{aligned} & a-b=0 \\ & a-2b+2=0 \\ \end{aligned} \right.\Leftrightarrow \left[ \begin{aligned} & a=b \\ & a=2b-2 \\ \end{aligned} \right. $
+ Với $a=b$, ta có $\sqrt{2x-1}=\sqrt{x+1}\Leftrightarrow 2x-1=x+1\Leftrightarrow x=2 \, \left( \text{tm} \right)$.
+ Với $a=2b-2$, ta có $ \sqrt{2x-1}=2\sqrt{x+1}-2\Leftrightarrow \sqrt{2x-1}+2=2\sqrt{x+1}\Leftrightarrow 2x-1+4\sqrt{2x-1}+4=4\left( x+1 \right)$
$\Leftrightarrow 2x+1=4\sqrt{2x-1}\Leftrightarrow 4{{x}^{2}}+4x+1=32x-16\Leftrightarrow 4{{x}^{2}}-28x+17=0\Leftrightarrow \left[ \begin{aligned} & x=\dfrac{7+4\sqrt{2}}{2} \, \left( \text{tm} \right) \\ & x=\dfrac{7-4\sqrt{2}}{2} \, \left( \text{ktm} \right) \\ \end{aligned} \right. $.
Vậy phương trình có tập nghiệm là $S=\left\{ 2;\dfrac{7+4\sqrt{2}}{2} \right\}$.
2. Ta có: $a+b+c=3\Rightarrow \left\{ \begin{aligned} & a+b=3-c \\ & b+c=3-a \\ & a+c=3-b \\ \end{aligned} \right.$.
Vì $a,$ $b,$ $c$ dương nên $a+b\ge 2\sqrt{ab}\Rightarrow 3-c\ge 2\sqrt{ab}\Rightarrow \sqrt{ab}\le \dfrac{3-c}{2}$.
Tương tự, ta có: $\sqrt{bc}\le \dfrac{3-a}{2}$; $\sqrt{ac}\le \dfrac{3-b}{2}$.
Suy ra $\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\le \dfrac{9-\left( a+b+c \right)}{2}=\dfrac{9-3}{2}=3$.
Ta có $\dfrac{b\sqrt{a}}{1+b}\le \dfrac{b\sqrt{a}}{2\sqrt{b}}=\dfrac{\sqrt{ab}}{2};$
$\dfrac{c\sqrt{b}}{1+c}\le \dfrac{c\sqrt{b}}{2\sqrt{c}}=\dfrac{\sqrt{bc}}{2};$
$\dfrac{a\sqrt{c}}{1+a}\le \dfrac{a\sqrt{c}}{2\sqrt{a}}=\dfrac{\sqrt{ac}}{2}$
Suy ra $\dfrac{b\sqrt{a}}{1+b}+\dfrac{c\sqrt{b}}{1+c}+\dfrac{a\sqrt{c}}{1+a}\le \dfrac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{2}\le \dfrac{3}{2}$.
Vậy $P\ge \dfrac{2021}{3}-\dfrac{3}{2}=\dfrac{4033}{6}$.
Dấu "=" xảy ra khi $a=b=c=1$.
