Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

a) $\left(27 x^{3}-64 y^{3}\right) \, : \, (3 x-4 y)$

$=(3 x-4 y)\left(9 x^{2}+12 x y+16 y^{2}\right) \, : \, (3 x-4 y)$ 

$= 9 x^{2}+12 x y+16 y^{2}$.

b) $(x+3)^{2}+(x-3)^{2}+2\left(x^{2}-9\right)$

$= x^{3}+9 x^{2}+27 x+27+x^{3}-9 x^{2}+27 x-27+2 x^{2}-18$

$= \left(x^{3}+x^{3}\right)+\left(9 x^{2}-9 x^{2}+2 x^{2}\right)+(27 x+27 x)+(27-27-18)$ 

$= 2 x^{3}+2 x^{2}+54 x-18$ 

c) $(4 x-1)^{3}-(4 x-4)\left(16 x^{2}+3\right)$

$= 64 x^{3}-48 x^{2}+12 x-1-\left(64 x^{3}+12 x-64 x^{2}-12\right)$ 

$= 64 x^{3}-48 x^{2}+12 x-1-64 x^{3}-12 x+64 x^{2}+12$

$= \left(64 x^{3}-64 x^{3}\right)+\left(-48 x^{2}+64 x^{2}\right)+(12 x-12 x)+(-1+12)$

$= 12 x^{2}+11$.

Hướng dẫn giải:

a) $6 x^{2}-(2 x-3)(3 x+2)=1$

$6 x^{2}-\left(6 x^{2}+4 x-9 x-6\right)=1$

$6 x^{2}-6 x^{2}-4 x+9 x+6=1$

$5 x=-5$

$x=-1$

Vậy $x=-1$.

b) $\left(x+\dfrac{1}{2}\right)^{2}-\left(x+\dfrac{1}{2}\right)(x+6)=8$

$x^{2}+x+\dfrac{1}{4}-\left(x^{2}+6 x+\dfrac{1}{2} x+3\right)=8$

$x^{2}+x+\dfrac{1}{4}-x^{2}-6 x-\dfrac{1}{2} x-3=8$

$-\dfrac{11}{2} x=\dfrac{43}{4}$

Vậy $x=-\dfrac{43}{22}$.

Hướng dẫn giải:

a) $M$ xác định khi $3 x \neq 0$; $x+1 \neq 0$ và $2-4 x \neq 0$

Hay $x \neq 0$; $x \neq-1$; $x \neq \dfrac{1}{2}$

Với $x \neq 0; \, x \neq-1; \, x \neq \dfrac{1}{2}$ ta có:

$M=\left(\dfrac{x+2}{3 x}+\dfrac{2}{x+1}-3\right) \, : \, \dfrac{2-4 x}{x+1}-\dfrac{3 x-x^2+1}{3 x} $

$=\left[\dfrac{(x+2)(x+1)+2 .3 x-3 .3 x(x+1)}{3 x(x+1)}\right] \, : \, \dfrac{2-4 x}{x+1}-\dfrac{3 x-x^2+1}{3 x}$

$=\left[\dfrac{x^2+2 x+x+2+6 x-9 x^2-9 x}{3 x(x+1)}\right] \, : \, \dfrac{2-4 x}{x+1}-\dfrac{3 x-x^2+1}{3 x} $

$=\dfrac{2-8 x^2}{3 x(x+1)}. \dfrac{x+1}{2(1-2 x)}-\dfrac{3 x-x^2+1}{3 x}$

$=\dfrac{2\left(1-4 x^2\right)}{3 x} . \dfrac{1}{2(1-2 x)}-\dfrac{3 x-x^2+1}{3 x} $

$=\dfrac{2(1+2 x)(1-2 x)}{3 x} . \dfrac{1}{2(1-2 x)}-\dfrac{3 x-x^2+1}{3 x} $

$=\dfrac{1+2 x}{3 x}-\dfrac{3 x-x^2+1}{3 x}$

$=\dfrac{x^2-x}{3 x}=\dfrac{x(x-1)}{3 x}=\dfrac{x-1}{3}.$

Vậy với $x \neq 0$; $x \neq-1$; $x \neq \dfrac{1}{2}$ thì $M=\dfrac{x-1}{3}$.

b) Để $M=2 \, 006$ thì $\dfrac{x-1}{3}=2 \, 006$

$x-1=6 \, 018$

$x=6 \, 019$ (tmđk).

Vậy khi $x=6 \, 019$ thì $M=2 \, 006$

Hướng dẫn giải:

a) Thị trường Thái Lan cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 là nhiều nhất.

Thị trường Trung Quốc cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 là ít nhất.

b) Tổng lượng tinh bột sắn mà các thị trường cung cấp cho Đài Loan trong 9 tháng năm 2022 là

218 155 + 24 859 + 3 447 + 2 983 + 483 = 249 927 (tấn).

Thị trường Việt Nam cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 chiếm

24 859 : 249 927 = 9,9%

Hướng dẫn giải:

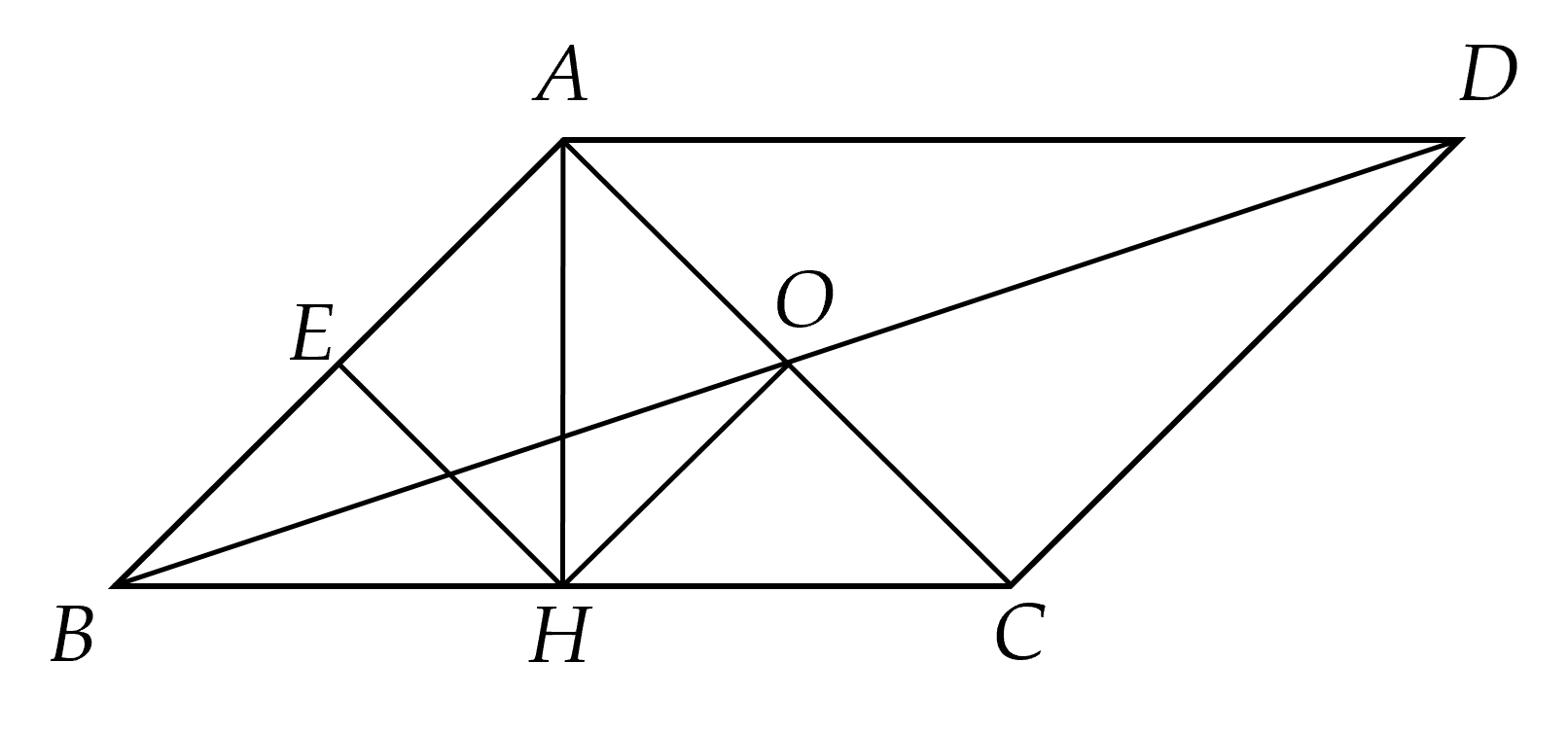
a) Xét tứ giác $ABCD$ có $OA=OC$; $OB=OD$ (gt) 

Suy ra $A B C D$ là hình bình hành (dhnb)

b) $A B C D$ là hình bình hành suy ra $AD$ // $BC$ hay $AD$ // $HC$ (1)

Mà $AH$ là đường cao của $\triangle ABC$ suy ra $\widehat{AHC}=90^{\circ}$ (2)

Từ (1) và (2) ta có $ A H C D$ là hình thang vuông.

c) Xét $\triangle {AHB}$ vuông tại ${H}$ có $\widehat{{ABH}}=45^{\circ}$ (do $\triangle {ABC}$ vuông cân tại ${A}$ )

Suy ra $\triangle {AHB}$ vuông cân tại ${H}$.

Suy ra ${HE}$ vừa là trung tuyến vừa là đường cao $\triangle {AHB}$

Suy ra ${HE} \perp {AB}$ hay $\widehat{{AEH}}=90^{\circ}$

Chứng minh tương tự $\widehat{{AOH}}=90^{\circ}$

Xét tứ giác ${AOHE}$ có

$\widehat{{EAO}}=\widehat{{AEH}}=\widehat{{AOH}}=90^{\circ}$

Suy ra ${AOHE}$ là hình chữ nhật (3)

Xét $\triangle {ABC}$ vuông cân tại ${A}$ có ${AH}$ là đường cao

Suy ra $ {AH}$ là phân giác $\widehat{{BAC}}$ (4)

Từ (3) và (4) ta có $A O H E$ là hình vuông.

Hướng dẫn giải:

$x^2+x y+2 \, 023 x+2 \, 022 y+2 \, 023 = 0$

$x^2+x y+x + 2 \, 022 x+2 \, 022 y+2 \, 022 + 1 = 0$

$x(x+y+1)+2022(x+y+1)=-1$

$(x+2022)(x+y+1)=-1$ (1)

Vì $x$, $y$ là số nguyên nên từ (1) suy ra:

+ TH1: $x + 2 \, 022 = 1$ và $x + y + 1 = -1$

Suy ra $x = -2 \, 021$ và $y = 2 \, 019$.

+ TH2: $x + 2 \, 022 = -1$ và $x + y + 1 = 1$

Suy ra $x = -2 \, 023$ và $y = 2 \, 023$.