Phương trình quy về phương trình bậc hai (nâng cao) SVIP

Tích các nghiệm của phương trình $\sqrt{x^2 + x + 1} = x^2 + x - 1$ bằng

Số nghiệm của phương trình $x^2-3 x+86-19 \sqrt{x^2-3 x+16}=0$ là

Phương trình $\sqrt{x-2}+\sqrt{x^2-x+1}=2 x-1+\sqrt{x-2}$ có số nghiệm là

Số nghiệm phương trình $(x+1) \sqrt{6 x^2-6 x+25}=23 x-13$ là

Cho tứ giác $A B C D$ có $A B \perp C D$; $A B=2$; $B C=13$; $C D=8$; $D A=5$. Gọi $H$ là giao điểm của $A B$ và $C D$ và đặt $x=A H$.

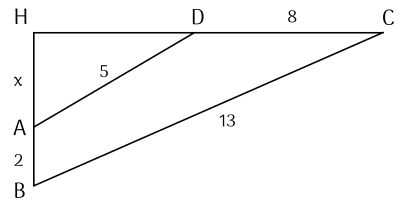
Diện tích tứ giác $A B C D$ bằng

Số nghiệm của phương trình $(x-2) \sqrt{2 x+7}=x^2-4$ là

Nghiệm của phương trình $2 x+3+(x+1) \sqrt{x^2+6}+(x+2) \sqrt{x^2+2 x+9}=0$, $(x \in \mathbb{R})$ là

Cho phương trình $\sqrt{-x^2+4 x-3}=\sqrt{2 m+3 x-x^2}$ (1). Để phương trình (1) có nghiệm thì $m \in[a ; b]$. Giá trị $a^2+b^2$ bằng

Với mọi giá trị dương của $m$ phương trình $\sqrt{x^2-m^2}=x-m$ luôn có số nghiệm là

Giá trị tham số $m$ để phương trình $\sqrt{2{x}^2-x-2 m}=x-2$ có nghiệm là