Số vô tỉ. Căn bậc hai số học SVIP

1. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ

Với một số hữu tỉ  \(\dfrac{a}{b}\) , ta có \(2\) trường hợp sau:

Trường hợp 1: Nếu  \(\dfrac{a}{b}\)  bằng một số thập phân thì kết quả của phép chia  \(\dfrac{a}{b}\)  là số thập phân bằng với phân số thập phân đó.

Ví dụ: \(\dfrac{1}{2}=\dfrac{5}{10}=0,5;\dfrac{41}{20}=\dfrac{205}{100}=2,05.\)

Trường hợp 2: Nếu \(\dfrac{a}{b}\)  không bằng bất cứ phân số thập phân nào thì kết quả của phép chia  \(\dfrac{a}{b}\)không bao giờ dừng và có chữ số hoặc cụm chữ số sau dấu phẩy lặp đi lặp lại.

Ví dụ:

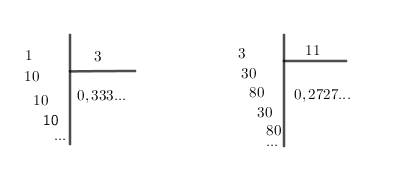
Khi đó, ta viết: \(\dfrac{1}{3}=0,333....=0,\left(3\right);\) \(\dfrac{3}{11}=0,2727...=0,\left(27\right).\)

Các số \(0,\left(3\right);0,\left(27\right)\) được gọi là số thập phân vô hạn tuần hoàn và chữ số hay cụm chữ số lặp đi lặp lại như \(\left(3\right);\left(27\right)\) được họi là chu kì.

Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn

2. SỐ VÔ TỈ

Hình vuông trong hình bên có diện tích bằng \(2\) \(dm^2\). Nếu độ dài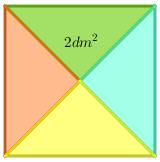

cạnh hình vuông đó là \(x\) \(\left(dm\right)\)\(\left(x>0\right)\) thì \(x^2=2.\)

Người ta đã chứng minh được rằng không có số hữu tỉ nào mà bình phương bằng \(2\) và tìm được những chữ số thập phân đầu tiên của \(x\) là: \(x=1,4142135623730950488016887...\)

Người ta đã chứng minh được số này là một số thập phân vô hạn mà ở phần thập phan của nó không có một chu kì nào cả. Đó là một số thập phân vô hạn không tuần hoàn.

Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.

Tập hợp các số vô tỉ được kí hiệu là \(I\).

3. CĂN BẬC HAI SỐ HỌC 

Ta có, số dương \(4\) thoả mãn \(4^2=16\), ta nói \(4\) là căn bậc hai số học của \(16\). Tương tự, số dương \(0,5\) thoả mãn \(\left(0,5\right)^2=0,25\), ta nói  \(0,5\) là căn bậc hai số học của \(0,25.\)

Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \(x^2=a.\)

Ta dùng kí hiệu \(\sqrt{a}\) để chỉ căn bậc hai số học của \(a\).

Người ta chứng minh được rằng:

Một số không âm \(a\) có đúng một căn bậc hai số học.

Chú ý: 

- Số âm không có căn bậc hai số học.

- Ta có \(\sqrt{a}\ge0\) với mọi số \(a\) không âm.

- Với mọi số không âm \(a\), ta luôn có \(\left(\sqrt{a}\right)^2=a.\)

4. TÍNH CĂN BẬC HAI SỐ HỌC BẰNG MÁY TÍNH CẦM TAY

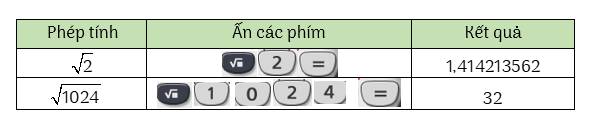
Ta có thể sử dụng loại máy tính cầm tay thích hợp để tính căn bậc hai số học của một số không âm. Chẳng hạn: